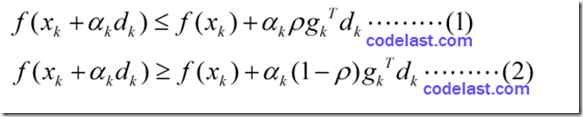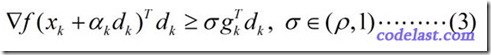Armijo-Goldstein准则与Wolfe-Powell准则
Armijo-Goldstein准则与Wolfe-Powell准则是不精确的一维搜索的两大准则。
之所以要遵循这些准则是为了能使算法收敛(求最优解)。即要使我们的不精确的一维搜索的步长满足一定的规则,使之后的求最优解的过程不至于因为步长过大或者过小而不收敛。
Armijo-Goldstein准则
Armijo-Goldstein准则的核心思想有两个:①目标函数值应该有足够的下降;②一维搜索的步长α不应该太小。
我们来看看Armijo-Goldstein准则的数学表达式:
其中, 0<ρ<12
1)为什么要规定 ρ∈(0,0.5) 这个条件?其实可以证明:如果没有这个条件的话,将影响算法的超线性收敛性。具体的证明过程,大家可以参考袁亚湘写的《最优化理论与方法》一书,我没有仔细看,我觉得对初学者,不用去管它。
(2)第1个不等式的左边式子的泰勒展开式为:
f(xk+αkdk)=f(xk)+αkgkTdk+o(αk)
去掉高阶无穷小,剩下的部分为: f(xk)+αkgkTdk
而第一个不等式右边与之只差一个系数 ρ
我们已知了 gkTdk<0 (这是 dk 为下降方向的充要条件),并且 ρ∈(0,0.5) ,因此,1式右边仍然是一个比 f(xk) 小的数,即:
f(xk)+αkρgkTdk<f(xk)
也就是说函数值是下降的(下降是最优化的目标)。
(3)由于 ρ∈(0,0.5) 且 gkTdk<0 ( dk 是一个下降方向的充要条件),故第2个式子右边比第1个式子右边要小,即:
αk(1−ρ)gkTdk<αkρgkTdk<0
如果步长 α 太小的话,会导致这个不等式接近于不成立的边缘。因此,式2就保证了 α 不能太小。
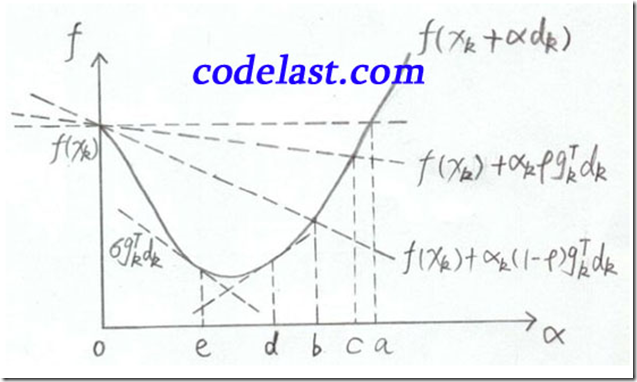
我还要把很多书中都用来描述Armijo-Goldstein准则的一幅图搬出来说明一下
横坐标是 α ,纵坐标是 f ,表示在 xk,dk 均为常量、 α 为自变量变化的情况下,目标函数值随之变化的情况。
之所以说 xk,dk 均为常量,是因为在一维搜索中,在某一个确定的点 xk 上,搜索方向 dk 确定后,我们只需要找到一个合适的步长 α 就可以了。
当 x 为常量, α 为自变量时, f(x+αd) 可能是非线性函数(例如目标函数为 y=x2 时)。因此图中是一条曲线。
右上角的 f(xk+αdk) 并不是表示一个特定点的值,而是表示这条曲线是以 α 为自变量、 xk,dk 为常量的函数图形。
当 α=0 时,函数值为 f(xk) ,如图中左上方所示。水平的那条虚线是函数值为 f(xk) 的基线,用于与其他函数值对比。
f(xk)+αkρgkTdk 那条线在 f(xk) 下方(前面已经分析过了,因为 gkTdk<0 ), f(xk)+αk(1−ρ)gkTdk 又在 f(xk)+αkρgkTdk 的下方(前面也已经分析过了),所以Armijo-Goldstein准则可能会把极小值点(可接受的区间)判断在区间bc内。显而易见,区间bc是有可能把极小值排除在外的(极小值在区间ed内)。
所以,为了解决这个问题,Wolfe-Powell准则应运而生。
Wolfe-Powell准则
Wolfe-Powell准则也有两个数学表达式,其中,第一个表达式与Armijo-Goldstein准则的第1个式子相同,第二个表达式为
这个式子已经不是关于函数值的了,而是关于梯度的。
此式的几何解释为:可接受点处的切线斜率≥初始斜率的 σ 倍。
上面的图已经标出了 σgTkdk 那条线(即 e 点处的切线),而初始点( α=0 的点)处的切线是比 e 点处的切线要“斜”的,由于 σ∈(ρ,1) ,使得 e 点处的切线变得“不那么斜”了——不知道这种极为通俗而不够严谨的说法,是否有助于你理解。
这样做的结果就是,我们将极小值包含在了可接受的区间内( e 点右边的区间)。
Wolfe-Powell准则到这里还没有结束!在某些书中,你会看到用另一个所谓的“更强的条件”来代替(3)式,即: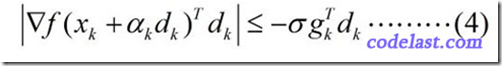
这个式子和(3)式相比,就是左边加了一个绝对值符号,右边换了一下正负号(因为 gTkdk<0 ,所以 −σgTkdk>0 )。
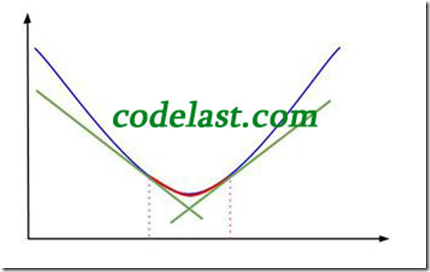
这样做的结果就是:可接受的区间被限制在了 [b,d] 内,如图:
图中红线即为极小值被“夹击”的生动演示。