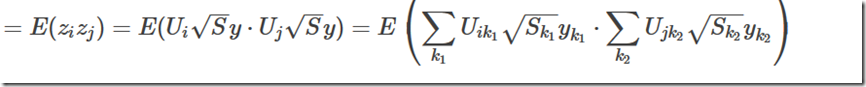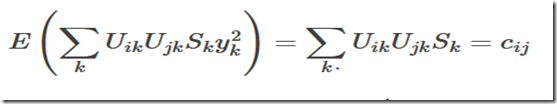高斯过程(GP)
随机过程基本概念:
随机过程是一个比随机变量更广泛的概念。在概率论中,通常研究一个或多个这样有限个数的随机变量,即使在大数定律和中心极限定理中考虑了无穷多个随机变量,但也要假设随机变量之间互相独立。而随机过程主要是研究无穷多个互相不独立的、有一定相关关系的随机变量。随机过程就是许多随机变量的集合,代表了某个随机系统随着某个指示向量的变化,这个指示向量常用的是时间向量

其中指标集合T:通常用的指标集合是代表时间,以实数或整数表示其元素。以实数形式表示时,随机过程即为连续随机过程;以整数形式表示时,为离散随机过程。
GP的定义:
对于任意集合S,S上的高斯过程(GP)是随机变量序列(Zt:t∈S)的一个集合,使得所有n∈N,所有t1,t2……,tn∈S,(Zt1,Zt2,……,Ztn)是多维高斯。
如果S集合中的元素个数是有限的,则Z是否为GP可以通过穷举判断其是否为多维高斯函数。如果S集合中元素的个数是无限的,则Z不能通过穷举获得,但是如果Z中的变量和某个高斯变量有直接联系的话,Z也有可能是S上的一个GP。
为什么要用高斯过程回归
现实实生活中,我们遇到的一个典型问题就是选择合适的模型拟合训练集中自变量 X 与因变量 y 之间的关系,并根据新的自变量 x 来预测对应的因变量 f
如果关系足够简单,那么线性回归就能实现很好的预测,但现实情况往往十分复杂,此时,高斯过程回归就为我们提供了拟合复杂关系(quadratic, cubic, or even nonpolynomial)的绝佳方法
什么是高斯过程回归
高斯过程可以看做是多维高斯分布向无限维的扩展,我们可以将 y=y1,y2,…,yn看作是从 n 维高斯分布中随机抽取的一个点
对高斯过程的刻画,如同高斯分布一样,也是用均值和方差来刻画。通常在应用高斯过程 f∼GP(m,K)的方法中,都是假设均值 m 为零,而协方差函数 K 则是根据具体应用而定
高斯回归的本质其实就是通过一个映射把自变量从低维空间映射到高维空间(类似于支持向量机中的核函数将低维线性不可分映射为高维线性可分),只需找到合适的核函数,就可以知道 p(f|x,X,y)的分布,最常用的就是高斯核函数
高斯过程回归的基本流程
再利用高斯过程回归时,不需要指明 f(x)的具体形式,如线性 f(x)=mx+c,或者二次
等具体式,n 个训练集的观测值 y1,y2,…,yn会被看做多维(n 维)高斯分布中采样出来的一个点
现在给定训练集 x1,x2,…,xn与对应的观测值y1,y2,…,yn,由于观测通常是带噪声的,所以将每个观测 y 建模为某个隐函数 f(x) 加上一个高斯噪声,即
其中,f(x)被假定给予一个高斯过程先验,即
其中协方差函数 k(x,x′)可以选择不同的单一形式,也可以采用协方差函数的组合形式,由于假设均值为零,因此最后结果的好坏很大程度上取决于协方差函数的选择。不同的协方差函数形式参见这篇文章对 Covariance Functions 的详细介绍。常见的协方差函数如下,参见 Wikipedia-Gaussian Process
存在定理说明:
对任意集合S中的单个元素都存在某个均值函数,以及对任意集合S中的2个元素都存在某个核函数(即协方差),则在S上一定存在一个高斯过程Z(t),其元素具有类似S形式的均值和方差。所以在给定集合S后,我们只需要给出一个一元的均值函数,一个二元的核函数表达式,就能构造出一个高斯过程。
常见的高斯过程

根据高斯分布的性质以及测试集和训练集数据来自同一分布的特点,可以得到训练数据与测试数据的联合分布为高维的高斯分布,有了联合分布就可以比较容易地求出预测数据 y∗ 的条件分布 p(y∗|y),对 y∗的估计的估计,我们就用分布的均值来作为其估计值
这里介绍一下通常情况对高斯函数采样的方法:首先我们知道任何高斯函数都可以写成标准高斯函数的线性组合,因此只要能够对标准高斯函数进行采样就OK了。其方法为:计算出标准高斯函数的分布函数,用[0,1]均匀分布随机发生器选择随机的值y,当做标准高斯函数的函数值,然后找到分布函数下对应的S就可以了,该点即为我们所需要的 Sample。
在常用的编程语言中,我们很容易生成一个高斯随机变量额采样(例如Matlab的randn函数),但如何生成给定均值函数和方差函数的高斯过程的采样呢?
问题
已知高斯过程的均值函数μ(x)以及相关函数k(t1,t2),欲生成N个符合此高斯过程的采样x(n),n=1,2,…..N均值函数只要最后累加即可。难点是如何生成满足相关性要求的采样。
步骤:
1.生成N个时间采样点t=[t1,t2,….,tN]
2.计算N个采样点之间的相关函数取值矩阵C:cij=k(ti,tj)
3.对C进行SVD分解,由于协方差矩阵对称,有C=USUT
3.生成N个独立同分布的高斯随机变量y=[y1,y2,….,yN],均值为0
证明
时间节点i处的随机变量Zi=UiSy,其中Ui为U的第i行,S为对角阵。
时间节点i和j处随机变量的相关:
由于y在每个时刻都独立,且上式得两个求和相乘中,只有k1=k2的项期望非0
所以
高斯过程回归与贝叶斯线性回归
两者其实比较相似,区别在于高斯过程回归中用核函数代替了贝叶斯线性回归中的基函数(其实也是核函数,线性核)。采用核函数定义高斯过程回归是一个比贝叶斯线性回归更通用的模型。
贝叶斯线性回归:数据D={(x1,y1),(x2,y2),…..,(xn,yn)} xi∈Rd y∈R y1,…..yn依赖于给定的W
P(yi|xi,w)=N(yi|WTx) 即
其中WTx是高斯分布,可以看作是高斯分布的线性组合,由此WT是一个多维的高斯分布
如果高斯过程为线性的,即它的sample是在高维空间中的平面,要求它的核函数满足k(xi,xj)d的形式,且均值函数为0,下面是它的证明过程:

既然已经得知yi的中心是在一个高维空间的平面上,所以当新来的数据后,就可以预测它的均值也在该平面对应的位置上,这就达到了回归的目的。
在将BLR(贝叶斯线性回归)扩展到GPR(高斯过程回归)前,来看看多维高斯分布的一些重要性质,第一个性质为两个相互独立的多维高斯分布A和B的和也是一个多维高斯分布C,且C的均值和方差都为A和B均值方差的和。第二个性质为:两个多维高斯分布之和构成的分布C而言,在已知一部分观察值C1的条件下,另一部分观察值C2的概率分布是一个多维高斯分布,且可以用A和B中对应的信息来表示。这2个性质的介绍如下:


接下来就是要怎样利用高斯过程进行回归运算了。高斯过程回归的模型如下:

其中的ya为需要预测的值,yb为观察到的值,当然了,xa和xb也是观察值。由前面博文机器学习&数据挖掘笔记_10(高斯过程简单理解)中介绍的高斯过程存在性定理可知,一旦我们确定了x上的u和k,就可以得到一个高斯过程Zx,此时的样本值Yi可以写成: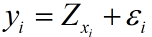 即两个独立的多维高斯变量之和。而利用上面多维高斯变量的性质,可推导出需要预测的ya在yb条件下的概率:
即两个独立的多维高斯变量之和。而利用上面多维高斯变量的性质,可推导出需要预测的ya在yb条件下的概率:
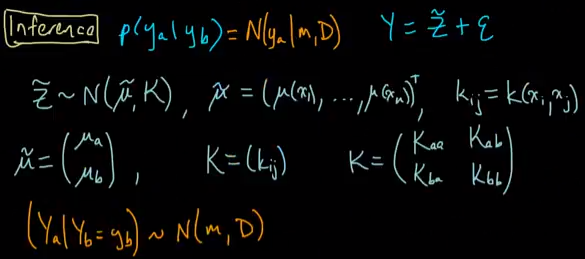
上面的m和D有解析表达式,因此可以直接求,里面的的变量都是已知的。其中的m就是我们回归预测的值,而D就是此时预测的误差,两者表达式和前面类似,如下:
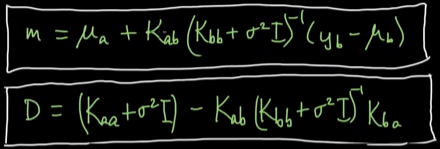
由贝叶斯线性回归和高斯过程回归的对比可知,贝叶斯线性回归是高斯过程回归中的一个子集,只是它用的是线性核而已,通过两者的公式就可以看出它们之间的关系:

上面是贝叶斯线性回归,下面是高斯过程回归。
总结




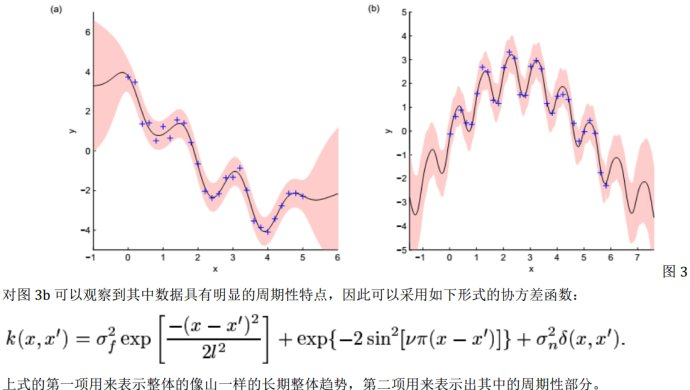
参考文献:
http://www.cnblogs.com/tornadomeet
http://www.gaussianprocess.org/
http://blog.sina.com.cn/s/blog_5033f3b40102vts4.html