【栈-01】栈题目解析
目录
- 739. 每日温度
- 面试题30. 包含min函数的栈/155. 最小栈
- 剑指 Offer 31. 栈的压入、弹出序列/946. 验证栈序列
简介:栈的特点是先进后出。
一、739. 每日温度
1.1 问题
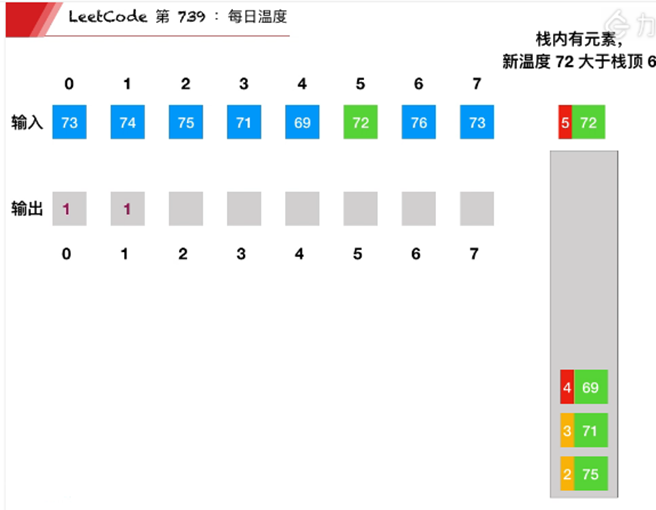
根据每日 气温 列表,请重新生成一个列表,对应位置的输出是需要再等待多久温度才会升高超过该日的天数。如果之后都不会升高,请在该位置用 0 来代替。
例如,给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73],你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。
提示:气温 列表长度的范围是 [1, 30000]。每个气温的值的均为华氏度,都是在 [30, 100] 范围内的整数。
1.2 单调栈
可以维护一个存储下标的单调栈,从栈底到栈顶的下标对应的温度列表中的温度依次递减。如果一个下标在单调栈里,则表示尚未找到下一次温度更高的下标。如下图所示:
1.3 步骤
正向遍历温度列表。对于温度列表中的每个元素 T[i],如果栈为空,则直接将 i 进栈,如果栈不为空,则比较栈顶元素 prevIndex 对应的温度 T[prevIndex] 和当前温度 T[i],如果 T[i] > T[prevIndex],则将 prevIndex 移除,并将 prevIndex 对应的等待天数赋为 i - prevIndex,重复上述操作直到栈为空或者栈顶元素对应的温度小于等于当前温度,然后将 i 进栈。
1.4 原理
为什么可以在弹栈的时候更新 ans[prevIndex] 呢?因为在这种情况下,即将进栈的 i 对应的 T[i] 一定是 T[prevIndex] 右边第一个比它大的元素,试想如果 prevIndex 和 i 有比它大的元素,假设下标为 j,那么 prevIndex 一定会在下标 j 的那一轮被弹掉。
由于单调栈满足从栈底到栈顶元素对应的温度递减,因此每次有元素进栈时,会将温度更低的元素全部移除,并更新出栈元素对应的等待天数,这样可以确保等待天数一定是最小的。
不想看文字,可以看看动态画的: https://leetcode-cn.com/problems/daily-temperatures/solution/leetcode-tu-jie-739mei-ri-wen-du-by-misterbooo/
1.5 代码
class Solution:
def dailyTemperatures(self, T: List[int]) -> List[int]:
n,stack,res = len(T),[],[0]*len(T)
for i in range(n):
while stack and T[i] > T[stack[-1]]: #和栈顶比较,上图中的4(69)
pre_index = stack.pop() #满足条件,则出栈,将下标给出 注意这里是pop 不是[-1]
res[pre_index] = i - pre_index
stack.append(i) #stack存入序号
return res
二、面试题30. 包含min函数的栈/155. 最小栈
2.1 题目
定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中,调用 min、push 及 pop 的时间复杂度都是 O(1)。
示例:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.min(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.min(); --> 返回 -2.
2.2 代码
class MinStack:
def __init__(self):
"""
initialize your data structure here.
"""
self.stackformin = [] #用于存放最小值序列
self.stack = []
def push(self, x: int) -> None:
self.stack.append(x)
if not self.stackformin or self.stackformin[-1] >= x: #注意这里有个等号,否则出错
self.stackformin.append(x)
def pop(self) -> None:
if self.stack.pop() == self.stackformin[-1]: #若删除的是最小的
self.stackformin.pop()
def top(self) -> int:
return self.stack[-1] #注意这里有return
def min(self) -> int:
return self.stackformin[-1] #注意这里有return
三、剑指 Offer 31. 栈的压入、弹出序列/946. 验证栈序列
3.1 题目
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如,序列 {1,2,3,4,5} 是某栈的压栈序列,序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列,但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。
示例 1:
输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出:true
解释:我们可以按以下顺序执行:push(1), push(2), push(3), push(4), pop() -> 4,push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1
示例 2:
输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出:false
解释:1 不能在 2 之前弹出。
3.2 代码
算法流程:
- 初始化: 辅助栈 stack ,弹出序列的索引 i ;
- 遍历压栈序列: 各元素记为 num ;【元素 num 入栈;循环出栈:若 stack 的栈顶元素 == 弹出序列元素 popped[i] ,则执行出栈与 i++ ;】
- 返回值: 若 stack 为空,则此弹出序列合法。

class Solution:
def validateStackSequences(self, pushed: List[int], popped: List[int]) -> bool:
stack = []
j = 0
for x in pushed:
stack.append(x)
while stack and stack[-1]==popped[j]:
stack.pop()
j += 1
return not stack


