【ML-13-7】隐马尔科夫模型HMM--词性标注任务
自然语言处理中经典的隐马尔科夫模型(HMM)。HMM早期在语音识别、分词等序列标注问题中有着广泛的应用。
了解HMM的基础原理以及应用,对于了解NLP处理问题的基本思想和技术发展脉络有很大的好处。本文会详细讲述HMM的基本概念和原理,并详细介绍其在分词中的实际应用。
一、HMM简介
HMM是一种链式依赖模型,由隐含状态S、可观测状态O表现。具体有初始状态概率矩阵π、隐含状态转移概率矩阵A、可观测值转移矩阵B;π和A决定了状态序列,B决定观测序列,因此HMM可以使用三元符号表示,称为HMM的三元素: λ = (A, B,π)具体介绍,可见其他文章系列。
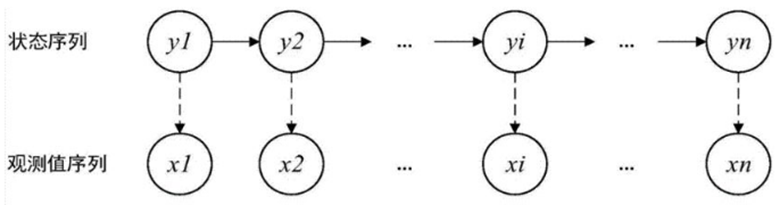
如图,HMM模型满足如下的性质:
(1) 它基于观测变量来推测未知变量;
(2) 状态序列满足马尔科夫性;
(3) 观测序列变量X在t时刻的状态仅由t时刻隐藏状态yt决定。
联合概率:
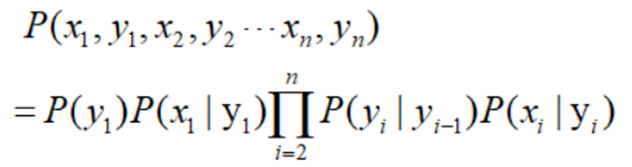
二、序列标注问题
序列标注定义可见另一篇文章。简单而言:
这里使用BMES标记。
B,即Begin,表示开始
M,即Mediate,表示中间
E,即End,表示结尾
S,即Single,表示单个字符
序列标注问题,就是对语句做出序列标注的判断,类似分类问题,但是又不是纯粹的分类任务,因为各部分标注之间有一定关系。这也是为何用马尔科夫模型式的原因:利用已知的观测序列来推断未知变量序列。主要涉及HMM-Viterbi算法。
举个例子吧:中文的句子"忆凡很喜欢自然语言处理"就是可以被观测到的序列,而其分词的标记序列就是未知的状态序列"忆凡/很/喜欢/自然语言/处理"这种分词方式对应的标记序列为"BESBEBMMEBS".
三、HMM模型的几个重要概率矩阵
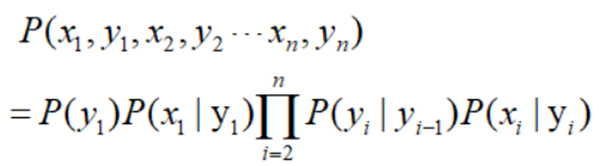
(1) 初始状态概率P(y1)
初始概率矩阵是指序列头的状态分布,以分词为例,就是每个句子开头,标记分别为BMES的概率。
(2) 状态转移概率P(yi|yi-1)
状态转移概率是指状态序列内,两个时刻内不同状态之间转移的状态分布。以分词为例,标记状态总共有BMES四种,因此状态转移概率构成了一个4*4的状态转移矩阵。这个矩阵描述了4种标记之间转化的概率。例如,P(yi="E"|yi-1="M")描述的i-1时刻标为"M"时,i时刻标记为"E"的概率。
(3) 输出观测概率P(xi|yi)
输出观测概率是指由某个隐藏状态输出为某个观测状态的概率。以分词为例,标记状态总共有BMES四种,词表中有N个字,则输出观测概率构成了一个4*N的输出观测概率矩阵。这个矩阵描述了4种标记输出为某个字的概率。例如,P(Xi="忆"|yi="B")描述的是i时刻标记为"B"时,i时刻观测到到字为"忆"的概率。
四、HMM在分词应用中的实战
假设有词序列Y = y1y2....yn,HMM分词的任务就是根据序列Y进行推断,得到其标记序列X= x1x2....xn,也就是计算这一个概率:
![]()
根据贝叶斯公式:
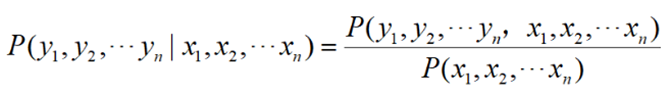
当语料确定时,上式分母为常数,只需要计算分子:
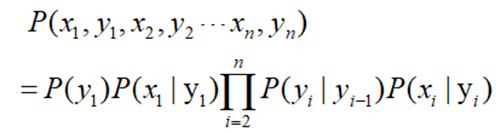
这个问题就变成了就三个矩阵问题和Viterbi算法了。
4.1 根据语料计算三个概率矩阵
当获得了分好词的语料之后,三个概率可以通过如下方式获得:
(1) 初始状态概率P(y1)
统计每个句子开头,序列标记分别为B,S的个数,最后除以总句子的个数,即得到了初始概率矩阵。
(2) 状态转移概率P(yi|yi-1)
根据语料,统计不同序列状态之间转化的个数,例如count(yi="E"|yi-1="M")为语料中i-1时刻标为"M"时,i时刻标记为"E"出现的次数。得到一个4*4的矩阵(注意BIOES为5*5的矩阵),再将矩阵的每个元素除以语料中该标记字的个数,得到状态转移概率矩阵。
(3) 输出观测概率P(xi|yi)
根据语料,统计由某个隐藏状态输出为某个观测状态的个数,例如count(xi="忆"|yi="B")为i时刻标记为"B"时,i时刻观测到字为"忆"的次数。得到一个4*N的矩阵,再将矩阵的每个元素除以语料中该标记的个数,得到输出观测概率矩阵。
我们看一下该部分的伪代码:
Pi = {k: v*1.0/line_num for k,v in Pi_dict.items()}
A = {k: { k1: v1/ Count_dict[k] for k1, v1 in v.items()}
for k, v in A_dict.items()
}
B= {k: { k1: v1/ Count_dict[k] for k1, v1 in v.items()}
for k,v in B_dict.items()
}
line_num 为预料中句子的个数;
Pi_dic 记录了语料中句子中开头标记的个数。
Count_dict 记录了预料中"BMES"四个标记的个数;
A_dict 记录了不同序列状态之间转化的个数;
B_dict 记录了不同隐藏状态输出为某个观测状态的个数。
4.2 维特比算法
求给定观测序列条件下,最可能出现的对应的隐藏状态序列。即给定模型λ=(A,B,π)和观测序列Q={q1,q2,...,qT},求给定观测序列条件概率P(I|Q,λ)最大的隐含状态序列 I。
HMM模型的解码问题最常用的算法是Viterbi(维特比)算法,当然也有其他的算法可以求解这个问题。同时维特比算法是一个通用的求序列最短路径的动态规划算法。具体可见这篇文章。
另外再举一个分词类的例子吧:
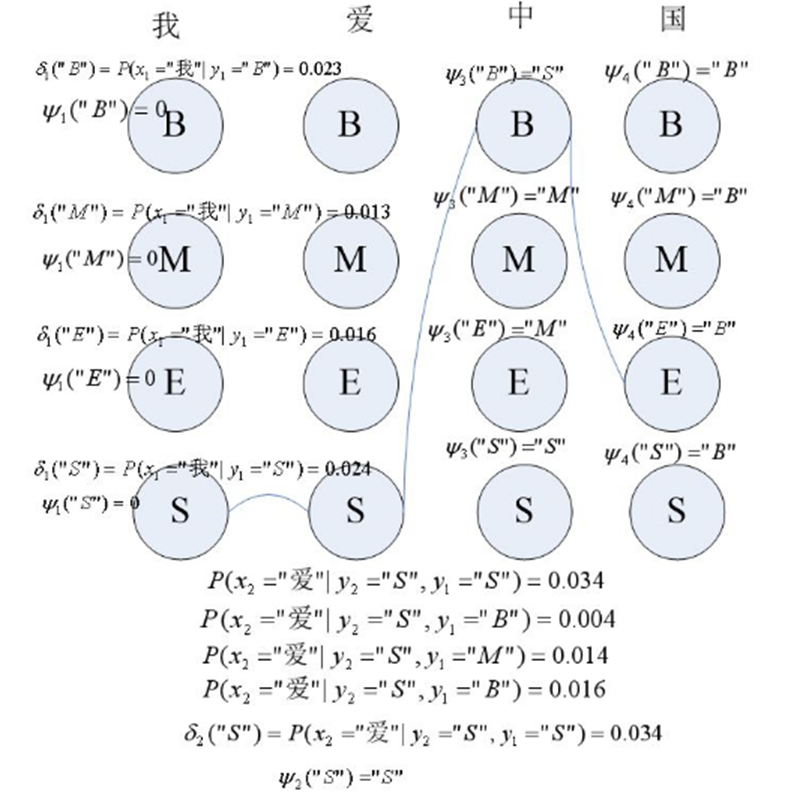
维特比算法是计算一个概率最大的路径,如图要计算"我爱中国"的分词序列:
第一个词为"我",通过初始概率矩阵和输出观测概率矩阵分别计算
delta1("B")=P(y1="S")P(x1="我"|y1="S"),
delta1("M")=P(y1="B")P(x1="我"|y1="B"),
delta1("E")=P(y1="M")P(x1="我"|y1="M"),
delta1("S")=P(y1="E")P(x1="我"|y1="E"),
并设kethe1("B")=kethe1("M")=kethe1("E")=kethe1("S")=0;
同理利用公式分别计算:
delta2("B"),delta2("M"),delta2("E"),delta2("S")。图中列出了delta2("S")的计算过程,就是计算:
P(y2="S"|y1="B")P(x2="爱"|y2="S")
P(y2="S"|y1="M")P(x2="爱"|y2="S")
P(y2="S"|y1="E")P(x2="爱"|y2="S")
P(y2="S"|y1="S")P(x2="爱"|y2="S")
其中 P(y2="S"|y1="S")P(x2="爱"|y2="S")的值最大,为0.034,因此delta2("S"),kethe2("S")="S",同理,可以计算出delta2("B"),delta2("M"),delta2("E")及kethe2("B"),kethe2("M"),kethe2("E")。
同理可以获得第三个和第四个序列标记的delta和kethe。
到最后一个序列,delta4("B"),delta4("M"),delta4("E"),delta4("S")中delta4("S")的值最大,因此,最后一个状态为"S"。
最后,回退,
i3 = kethe4("S") ="B"
i2 =kethe3("B") = "S"
i1 = kethe2("S") ="S"
求得序列标记为:"SSBE"。


