【树-03】树的题目解析
目录
- 剑指 Offer 55 - II. 平衡二叉树/110. 平衡二叉树
- 剑指 Offer 26. 树的子结构 (中等难度)
- 剑指 Offer 68 - I. 二叉搜索树的最近公共祖先
- 剑指 Offer 68 - II. 二叉树的最近公共祖先/236. 二叉树的最近公共祖先
- 剑指 Offer 36. 二叉搜索树与双向链表
一、剑指 Offer 55 - II. 平衡二叉树/110. 平衡二叉树
1.1 问题
输入一棵二叉树的根节点,判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]
3
/ \
9 20
/ \
15 7
返回 true 。
1.2 代码
class Solution: #注意调用函数时,需要用self,若是嵌套类型的方法定义,则不需要
def isBalanced(self, root: TreeNode) -> bool:
if not root :return True
if (abs(self.height(root.left)-self.height(root.right))>1):
return False
else:
return self.isBalanced(root.left) and self.isBalanced(root.right)
def height(self,root):
if not root : return 0
return 1+ max(self.height(root.left),self.height(root.right))
二、剑指 Offer 26. 树的子结构 (中等难度)
2.1 问题
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即 A中有出现和B相同的结构和节点值。
例如:
给定的树 A:
3
/ \
4 5
/ \
1 2
给定的树 B:
4
/
1
返回 true,因为 B 与 A 的一个子树拥有相同的结构和节点值。
示例 1:
输入:A = [1,2,3], B = [3,1]
输出:false
示例 2:
输入:A = [3,4,5,1,2], B = [4,1]
输出:true
2.2 代码(递归算法)
class Solution:
def isSubStructure(self, A: TreeNode, B: TreeNode) -> bool:
def recur(A,B):
if not B :return True
if not A or A.val != B.val :return False
return recur(A.left,B.left) and recur(A.right,B.right)
return bool(A and B) and (recur(A,B) or self.isSubStructure(A.left,B) or self.isSubStructure(A.right,B))
三、剑指 Offer 68 - I. 二叉搜索树的最近公共祖先
3.1 问题
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:"对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。"
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
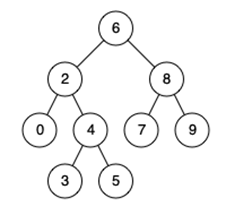
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
3.2 代码
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
if not root :return None
if p.val > q.val : # 保证 p.val < q.val
p,q = q,p
while root :
if root.val < p.val: # p,q 都在 root 的右子树中
root = root.right # 遍历至右子节点
if root.val > q.val:
root = root.left
else:
break
return root
四、剑指 Offer 68 - II. 二叉树的最近公共祖先/236. 二叉树的最近公共祖先
4.1 问题
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:"对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。"
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
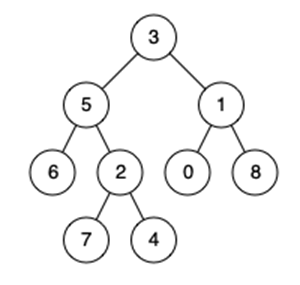
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
4.2 理解

4.2 代码
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
if not root or root == p or root == q: return root
left = self.lowestCommonAncestor(root.left, p, q)
right = self.lowestCommonAncestor(root.right, p, q)
if not left and not right: return # 1.
if not left: return right # 3.
if not right: return left # 4.
return root # 2. if left and right:
五、剑指 Offer 36. 二叉搜索树与双向链表
5.1 问题
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。

5.2 代码(中序遍历+递归)
大体思路要清楚:框架是中序遍历,写好中间部分即可:设置两个pre和cur,pre若为空,设置下头结点;不空,则进行互相指定。
不要忘记最后的head与最后的指定。
"""
# Definition for a Node.
class Node:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
"""
class Solution:
def treeToDoublyList(self, root: 'Node') -> 'Node':
def dfs(cur):
if not cur :return
dfs(cur.left)
if self.pre: #不为空,则互相指定
self.pre.right,cur.left = cur ,self.pre
else: #为空,记录头结点,这个走一遍
self.head = cur
self.pre = cur #保存后进行下一步推进
dfs(cur.right)
if not root :return
self.pre = None
dfs(root)
self.head.left,self.pre.right = self.pre,self.head
return self.head


