【树-01】树的介绍及题目解析
目录
- 树的简介
- 剑指 Offer 07. 重建二叉树/105. 从前序与中序遍历序列构造二叉树
- 剑指 Offer 27. 二叉树的镜像/226. 翻转二叉树
- 剑指 Offer 55 - I. 二叉树的深度/104. 二叉树的最大深度
- 剑指 Offer 34. 二叉树中和为某一值的路径/113. 路径总和 II
一、树的简介
1.1 二叉树的遍历
分为以下三种(按照跟的位置,决定前中后序排列):
- 前序遍历:遍历顺序规则为【根左右】
- 中序遍历:遍历顺序规则为【左根右】
- 后序遍历:遍历顺序规则为【左右根】
1.2 二叉查找树(英语:Binary Search Tree)
也称为 二叉搜索树、有序二叉树(Ordered Binary Tree)或排序二叉树(Sorted Binary Tree),是指一棵空树或者具有下列性质的二叉树:
若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
1.3 方法
- 递归,这种思路在解题过程中非常实用,而且可解读性很强,但是时间复杂度相对较高;
- 栈和队列(偶尔用到双向队列)
二、剑指 Offer 07. 重建二叉树/105. 从前序与中序遍历序列构造二叉树
1.1 问题
输入某二叉树的前序遍历和中序遍历的结果,请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
例如,给出
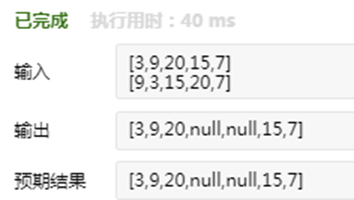
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树:
3
/ \
9 20
/ \
15 7
1.2 代码(使用递归)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
if not preorder:
return None
#创建当前节点
node = TreeNode(preorder[0])
#查找当前的根节点在中序遍历中的位置
index = inorder.index(preorder[0])
# 划分左右子树。序号节点的选取注意把握:中序【左根右】,前序【根左右】
left_in = inorder[:index] #左子树的中序遍历
right_in = inorder[index+1:] #右子树的中序遍历
left_pre = preorder[1:index+1] #左子树的前序遍历
right_pre = preorder[index+1:] #右子树的前序遍历
# 遍历创建子树
node.left = self.buildTree(left_pre, left_in)
node.right = self.buildTree(right_pre, right_in)
# 返回当前节点
return node
三、剑指 Offer 27. 二叉树的镜像/226. 翻转二叉树
2.1 问题
请完成一个函数,输入一个二叉树,该函数输出它的镜像。
例如输入:
4
/ \
2 7
/ \ / \
1 3 6 9
镜像输出:
4
/ \
7 2
/ \ / \
9 6 3 1
示例 1:
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
2.2 代码(递归实现)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def mirrorTree(self, root: TreeNode) -> TreeNode:
if not root:
return None
temp = root.left
root.left = self.mirrorTree(root.right)
root.right = self.mirrorTree(temp)
return root
四、剑指 Offer 55 - I. 二叉树的深度/104. 二叉树的最大深度
4.1 题目
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
4.2 代码一:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def maxDepth(self, root: TreeNode) -> int:
if not root: return 0
return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1
4.3 代码二:
方法二:层序遍历(BFS)
树的层序遍历 / 广度优先搜索往往利用 队列 实现。
关键点: 每遍历一层,则计数器 +1+1 ,直到遍历完成,则可得到树的深度。
算法解析:
- 特例处理: 当 root 为空,直接返回 深度 0 。
- 初始化: 队列 queue (加入根节点 root ),计数器 res = 0。
- 循环遍历: 当 queue 为空时跳出。
- 初始化一个空列表 tmp ,用于临时存储下一层节点;
- 遍历队列: 遍历 queue 中的各节点 node ,并将其左子节点和右子节点加入 tmp;
- 更新队列: 执行 queue = tmp ,将下一层节点赋值给 queue;
- 统计层数: 执行 res += 1 ,代表层数加 11;
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def maxDepth(self, root: TreeNode) -> int:
if not root: return 0
queue, res = [root], 0
while queue:
tmp = [] #清空,为下一层数据做准备
for node in queue:
if node.left: tmp.append(node.left)
if node.right: tmp.append(node.right)
queue = tmp #将下一层的数据都加入到queue中
res += 1
return res
五、剑指 Offer 34. 二叉树中和为某一值的路径/113. 路径总和 II
5.1 问题
给定一个二叉树和一个目标和,找到所有从根节点到叶子节点路径总和等于给定目标和的路径。说明: 叶子节点是指没有子节点的节点。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ / \
7 2 5 1
返回:
[
[5,4,11,2],
[5,8,4,5]
]
5.2 代码(递归方式)
先序遍历: 按照 "根、左、右" 的顺序,遍历树的所有节点。
路径记录: 在先序遍历中,记录从根节点到当前节点的路径。当路径为
① 根节点到叶节点形成的路径
② 各节点值的和等于目标值 sum 时
将此路径加入结果列表。
class Solution:
def pathSum(self, root: TreeNode, sum: int) -> List[List[int]]:
res,path = [],[]
def recur(root,tar):
if not root :
return
path.append(root.val)
tar -= root.val
if tar ==0 and not root.left and not root.right:
res.append(list(path)) #这里必须加上list
recur(root.left,tar)
recur(root.right,tar)
path.pop()
recur(root , sum)
return res


