【DP-03】动态规划算法题目解析
目录
- 面试题14- I. 剪绳子/343. 整数拆分
- 面试题42. 连续子数组的最大和/53. 最大子序和
- 面试题47. 礼物的最大价值
一、面试题14- I. 剪绳子/343. 整数拆分
1.1 问题:
给定一个正整数 n,将其拆分为至少两个正整数的和,并使这些整数的乘积最大化。 返回你可以获得的最大乘积。
示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
1.2 求解:
1)步骤一:定义子问题
假设n的最大值为f(n),可以将n拆分成i和n-i,问题变成 i乘以f(n-i),这样就变成了f(k),k<n的子问题了。
2)写出子问题的递推关系
和第一步一样,使用dp表示其值,但是要注意 i * (n - i) 本省也可能成为最大值;另外因为是遍历循环,要考虑计算过的dp[i],因此得到如下表达式:
dp[i] = max(dp[i], max(i * dp(n - i),i * (n - i)))
初始值:每个dp都设置为1
3)确定 DP 数组的计算顺序
而这里的 n 是什么呢?我们说了dp是自底向下的思考方式。因此这里的 n 实际上是 1,2,3,4... n。
自然地,我们用一层循环来生成上面一系列的 n 值。接着我们还要生成一系列的 i 值,注意到 n - i 是要大于 0 的,因此 i 只需要循环到 n - 1 即可。
4 )空间优化(可选)
因为要循环使用,所以无法进行空间优化
1.3 代码
class Solution:
def integerBreak(self, n: int) -> int:
dp=[1]*(n+1)
for i in range(3,n+1):
for j in range(1,i):
dp[i] = max(j*dp[i-j],j*(i-j),dp[i])
return dp[-1]
二、面试题42. 连续子数组的最大和/53. 最大子序和
2.1 问题:
输入一个整型数组,数组里有正数也有负数。数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
要求时间复杂度为O(n)。
示例1:
输入: nums = [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
2.2 求解:
问题比较简单,一维数组的问题。
1)步骤一:定义子问题
假设n的最大值为f(n),可以将n拆分成i和n-i,问题变成 i加上f(n-i)或直接是f(n-i),这样就变成了f(k),k<n的子问题了
2)写出子问题的递推关系
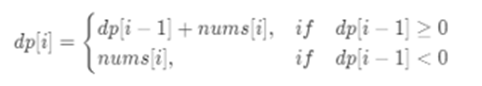
上面的进行简化:
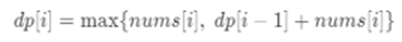
初始状态:将每个复制为0或数组的第一个值。
3)确定 DP 数组的计算顺序
很明显,使用自底向上的方式进行。具体代码见2.3的代码一
4 )空间优化(可选)
从代码也很明显看到,只用了dp[i-1]这个前置项,另外是最后输出的max(dp)也需要保留,其它是暂存也没有用到,所以可将其优化,将dp[i-1]用max_temp,最后的输出使用res。具体可见代码二。
2.3 代码
代码一:
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
n = len(nums)
if n == 0:return 0
else:
dp = [nums[0]] *(n)
for i in range(1,n): #注意这里不是n+1
dp[i] = max (dp[i-1]+nums[i],nums[i])
return max(dp)
代码二:
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
n = len(nums)
if n == 0:return 0
else:
max_temp = nums[0]
res = max_temp
for i in range(1,n):
max_temp = max (max_temp + nums[i],nums[i])
res = max(res,max_temp)
return res
三、面试题47. 礼物的最大价值
3.1 问题:
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?
示例 1:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物
3.2 求解:
是二维数组题,难度为中等偏上,和这题【1143. 最长公共子序列】类似
1)步骤一:定义子问题
题目说明:从棋盘的左上角开始拿格子里的礼物,并每次 向右 或者 向下 移动一格、直到到达棋盘的右下角。
根据题目说明,易得某单元格只可能从上边单元格或左边单元格到达。
很明显,缩小规模的子问题和原文题是等效的。
2)写出子问题的递推关系
定义二维矩阵,设动态规划矩阵 dp ,dp(i,j) 代表从棋盘的左上角开始,到达单元格 (i,j) 时能拿到礼物的最大累计价值。

3)确定 DP 数组的计算顺序
先行后列,从上到下进行计算即可。具体代码见3.3代码一。
4 )空间优化(可选)

对角进行替换,换成下图所示的例子,进一步优化空间:
| temp |
dp[j-1] | dp[j-1] |
只是用上面和左边的,所以可以重复利用,循环推进就可以了。具体见代码二。
3.3 代码
代码一:
class Solution:
def maxValue(self, grid: List[List[int]]) -> int:
m = len(grid)
n = len(grid[0])
dp = [[0]*(n+1) for _ in range(m+1)] #(m+1)(n+1)的矩阵
for i in range (1,m+1): #注意要从1开始,结束为m+1
for j in range(1,n+1):
dp[i][j] = max (dp[i-1][j],dp[i][j-1]) + grid[i-1][j-1]
return dp[-1][-1]
代码二:
class Solution:
def maxValue(self, grid: List[List[int]]) -> int:
m = len(grid)
n = len(grid[0])
dp = [0]*(n+1) #(n+1)的数组
for i in range (1,m+1): #注意要从1开始,结束为m+1
for j in range(1,n+1):
temp = dp[j] #这个也可省略,因为是循环更新,可以代表d[i-1][j]
dp[j] = max (temp,dp[j-1]) + grid[i-1][j-1]
return dp[-1]


