【DP-02】动态规划算法题目解析
目录
- 最长公共子序列
- 编辑距离
- 最长上升子序列
结合上一篇文章,再继续尝试解决动态规划题目
一、1143. 最长公共子序列
1.1 问题:
给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。
若这两个字符串没有公共子序列,则返回 0。
示例 1:
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace",它的长度为 3。
示例 2:
输入:text1 = "abc", text2 = "abc"
输出:3
解释:最长公共子序列是 "abc",它的长度为 3。
示例 3:
输入:text1 = "abc", text2 = "def"
输出:0
解释:两个字符串没有公共子序列,返回 0。
1.2 求解:
1)步骤一:定义子问题
要定义子问题,我们还是抓住这样一个子问题的基本性质:子问题是和原问题相似,但规模较小的问题。本体属于二维动态规划题目。

f(i,j) 表示长度为i和j的两个字符串的公共子串长度。
2)写出子问题的递推关系
这一步是求解动态规划问题的关键。二维的子问题有很多可能的递推关系,有些题目一目了然,有些则可能需要仔细推敲。 一般来说,我们首先思考能不能使用一种最简单的子问题递推关系:看当前子问题和前一个子问题的关系。如果是一维子问题,就是看 f(i)和 f(i-1)的关系;如果是二维子问题,则是看f(i,j)和f(i-1,j) 、f(i,j-1)、f(i-1,j-1) 的关系。LCS 问题就是这种简单递推关系的代表。
情况一:
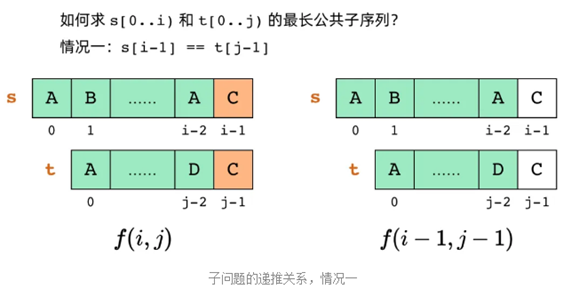
情况二:
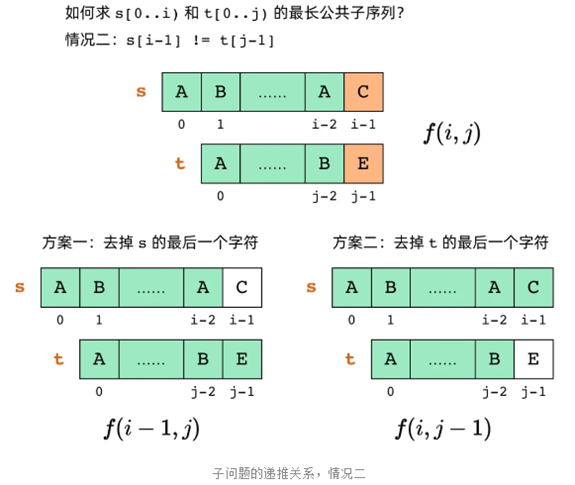
这样,我们得到的子问题递推关系为:
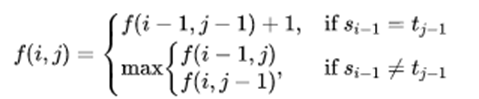
注意这里涉及到边界值:


3)确定 DP 数组的计算顺序
对于二维动态规划问题,我们仍然要坚持使用 DP 数组,用自底向上的顺序计算子问题。因为 DP 数组中的每一个元素都对应一个子问题,当子问题变成二维之后,DP 数组也需要是二维数组。在 DP 数组中,
Dp[i][j]对应子问题f(i,j)的值。

但是对于二维动态规划问题,我们需要有一定的方法来思考 DP 数组的计算顺序。
DP 数组计算顺序的基本原则是:当我们计算一个子问题时,它所依赖的其他子问题应该已经计算好了。 根据这个原则,我们思考三点内容。
第一点:DP 数组的有效范围是什么?
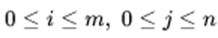
因此 dp = [[0]*(n+1) for _ in range(m+1)] 。定义数组为[m+1][n+1].
第二点:base case 和原问题在 DP 数组中在什么位置? 如下图所示,base case 位于 DP 数组的最左侧一列和最上方一行,而原问题则位于 DP 数组的右下角。
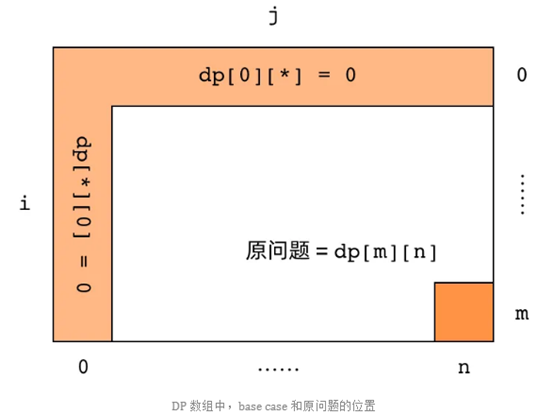
第三点:DP 数组的子问题依赖方向是什么? 观察子问题的递推关系,f(i,j)依赖:f(i-1,j) 、f(i,j-1)、f(i-1,j-1) 。
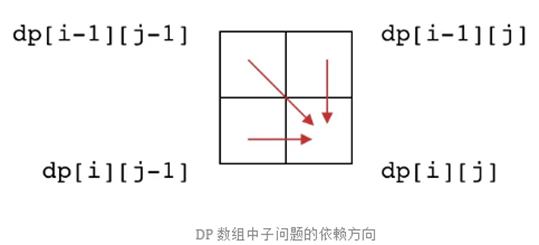
我们发现,子问题的依赖方向是向右、向下的,因此 DP 数组的计算顺序也应该是从左到右、从上到下。也就是说我们应该以这样的顺序遍历 DP 数组:
for i in range(1,m+1):
for j in range(1,n+1):
具体代码见1.3部分。
4 )空间优化(可选)
二维动态规划问题的 DP 数组变成了二维数组,空间复杂度更高了。因此,二维动态规划问题也更值得进行空间优化,降低空间复杂度。
不过,二维动态规划问题的空间优化有很多种方法,需要根据不同的情况灵活使用。空间优化的步骤是可选的,优化不优化都可以。 本题进行垂直方向压缩,也即是只取n+1维数组,如下图所示,具体代码见1.3部分。

最终变成以下表达式,后续根据这个向右滚动。
|
last |
temp |
|
dp[j-1] |
dp[j-1] |
需要注意的是,空间优化方法只能优化空间复杂度,不能优化时间复杂度。例如 LCS 问题在空间优化前后的复杂度为:
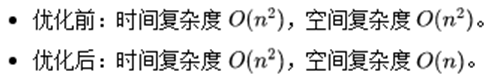
1.3 代码
1)优化前
class Solution(object): def longestCommonSubsequence(self, text1, text2): """ 子问题: f(i, j) = s[0..i) 和 t[0..j) 的最长公共子序列 f(0, *) = 0 f(*, 0) = 0 f(i, j) = f(i-1, j-1) + 1, if s[i-1] == t[j-1] max{ f(i-1, j), f(i, j-1) }, otherwise """ if not text1 or not text2: return 0 m = len(text1) n = len(text2) dp = [[0]*(n+1) for _ in range(m+1)] #[m+1][n+1]的矩阵 for i in range(1,m+1): for j in range(1,n+1): if text1[i-1] == text2[j-1]: dp[i][j] = 1 + dp[i-1][j-1] else: dp[i][j] = max(dp[i-1][j],dp[i][j-1]) return dp[m][n]
2)优化后
class Solution(object): def longestCommonSubsequence(self, text1, text2): """ 子问题: f(i, j) = s[0..i) 和 t[0..j) 的最长公共子序列 f(0, *) = 0 f(*, 0) = 0 f(i, j) = f(i-1, j-1) + 1, if s[i-1] == t[j-1] max{ f(i-1, j), f(i, j-1) }, otherwise """ if not text1 or not text2: return 0 m = len(text1) n = len(text2) dp = [0]*(n+1) # temp = 0 for i in range(1,m+1): last = 0 for j in range(1,n+1): temp =dp[j] if text1[i-1] == text2[j-1]: dp[j] = last + 1 else: dp[j] = max(temp,dp[j-1]) last = temp #向前滚动,temp的值赋值给last return dp[n]
二、leetcode72. 编辑距离
2.1 问题:
给你两个单词 word1 和 word2,请你计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
示例 1:
输入:word1 = "horse", word2 = "ros"
输出:3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
示例 2:
输入:word1 = "intention", word2 = "execution"
输出:5
解释:
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')
2.2 求解:
该问题较难,先分析如下:
如果你觉得从全局考虑很困难,就试试先不考虑全局,从局部入手。我们可以只考虑其中的「一步」,至于剩下的步骤,就交给其他子问题完成就行。对于编辑距离来说,这「一步」就是指「单次的编辑操作」。
这有点类似递归的思路。我只需要把当前这一步计算做好,然后相信递归函数能帮我做好剩下的计算。动态规划其实很像递归,只不过动态规划一般是自底向上计算,保存每个子问题。
1)步骤一:定义子问题
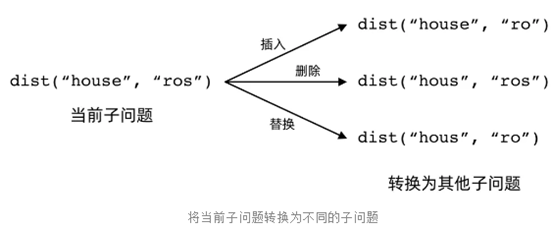
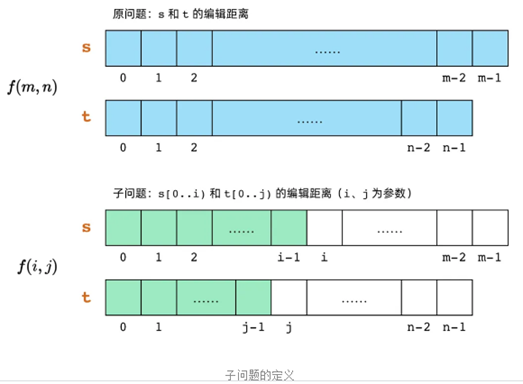
2)写出子问题的递推关系
dp[i][j] 代表 word1 到 i 位置转换成 word2 到 j 位置需要最少步数所以,
情况一,如下图当 word1[i] != word2[j],dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1
情况二,如下图所示:当 word1[i] == word2[j],dp[i][j] = dp[i-1][j-1];
其中,dp[i-1][j-1] 表示替换操作,dp[i-1][j] 表示删除操作,dp[i][j-1] 表示插入操作。补充理解如下:
以 word1 为 "horse",word2 为 "ros",且 dp[5][3] 为例,即要将 word1的前 5 个字符转换为 word2的前 3 个字符,也就是将 horse 转换为 ros,因此有:
(1) dp[i-1][j-1],即先将 word1 的前 4 个字符 hors 转换为 word2 的前 2 个字符 ro,然后将第五个字符 word1[4](因为下标基数以 0 开始) 由 e 替换为 s(即替换为 word2 的第三个字符,word2[2])
(2) dp[i][j-1],即先将 word1 的前 5 个字符 horse 转换为 word2 的前 2 个字符 ro,然后在末尾补充一个 s,即插入操作
(3) dp[i-1][j],即先将 word1 的前 4 个字符 hors 转换为 word2 的前 3 个字符 ros,然后删除 word1 的第 5 个字符
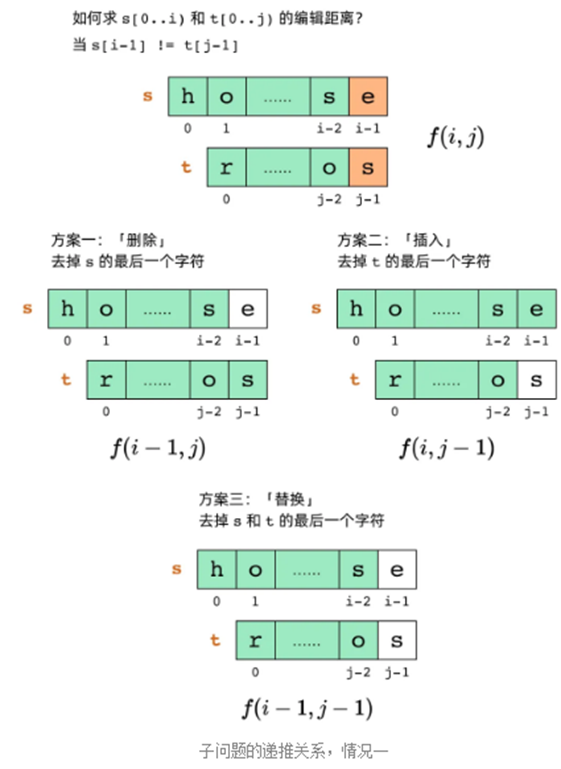
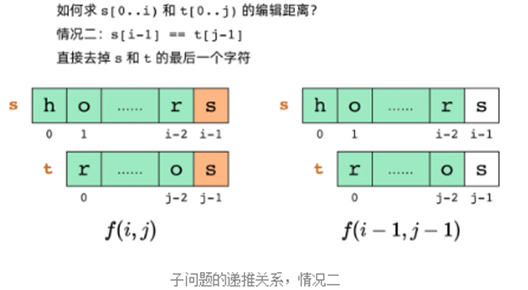
这样,我们得到最终的子问题递推关系为:

注意这里涉及到边界值:
f(0,j) = j
f(i,0) =i

3)确定 DP 数组的计算顺序
和第一章类似,f(i,j)依赖:f(i-1,j) 、f(i,j-1)、f(i-1,j-1) 。

具体代码可见2.3
4 )空间优化(可选)
编辑距离问题本身属于较难的题目,所以我们写出基本的解法就可以,一般面试中不会追问空间优化的方法。
2.3 代码
class Solution: def minDistance(self, word1: str, word2: str) -> int: n1 = len(word1) n2 = len(word2) dp = [[0] * (n2 + 1) for _ in range(n1 + 1)] # 第一行,初始化 for j in range(1, n2 + 1): dp[0][j] = dp[0][j-1] + 1 # 第一列,初始化 for i in range(1, n1 + 1): dp[i][0] = dp[i-1][0] + 1 for i in range(1, n1 + 1): for j in range(1, n2 + 1): if word1[i-1] == word2[j-1]: dp[i][j] = dp[i-1][j-1] else: dp[i][j] = min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1] ) + 1 #print(dp) return dp[-1][-1]
三、leetcode300. 最长上升子序列
3.1 问题:
给定一个无序的整数数组,找到其中最长上升子序列的长度。
示例:
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。
说明:
可能会有多种最长上升子序列的组合,你只需要输出对应的长度即可。
你算法的时间复杂度应该为 O(n^2) 。
进阶: 你能将算法的时间复杂度降低到 O(n log n) 吗?
注意:这里不用紧邻,只要前后关系即可。
3.2 求解:
1)步骤一:定义子问题
每个问题可以看成规模更小的子问题,使用DP[i]表示nums前i个数字的最长子序列长度。
2)写出子问题的递推关系
每次可能用到所有的dp[i]的数据。

3)确定 DP 数组的计算顺序
根据当前i的值,和递归后的值进行比较,取最大的。
4 )空间优化(可选)
每次都要用到之前的数据,本题不可优化。
3.3 代码
# Dynamic programming. class Solution: def lengthOfLIS(self, nums: List[int]) -> int: if not nums: return 0 dp = [1] * len(nums) for i in range(len(nums)): for j in range(i): if nums[j] < nums[i]: # 如果要求非严格递增,将此行 '<' 改为 '<=' 即可。 dp[i] = max(dp[i], dp[j] + 1) return max(dp)
参考文献:
【2】经典动态规划:编辑距离


