格拉姆矩阵（Gram matrix）详细解读

目录

• 基础知识-向量的内积
• Gram matrix介绍
• Gram matrix的应用-风格迁移

一、基础知识-向量的内积

1.1 向量的内积定义：也叫向量的点乘，对两个向量执行内积运算，就是对这两个向量对应位一一相乘之后求和的操作，内积的结果是一个标量。

1.2 实例：

a和b的内积公式为：

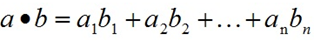
1.3 作用：

内积判断向量a和向量b之间的夹角和方向关系

• a·b>0    方向基本相同，夹角在0°到90°之间
• a·b=0    正交，相互垂直  
• a·b<0    方向基本相反，夹角在90°到180°之间 

Gram矩阵是两两向量的内积组成，所以Gram矩阵可以反映出该组向量中各个向量之间的某种关系。

二、Gram matrix介绍

2.1 定义

n维欧式空间中任意k个向量之间两两的内积所组成的矩阵，称为这k个向量的格拉姆矩阵(Gram matrix)，很明显，这是一个对称矩阵。

更加直观的理解：

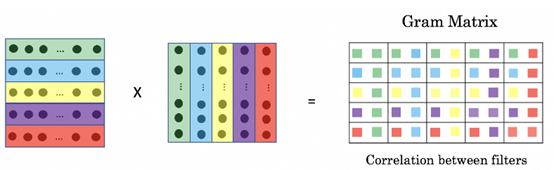
2.2 计算和特征表示

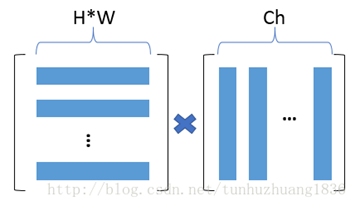
输入图像的feature map为[ ch, h, w]。我们经过flatten（即是将h*w进行平铺成一维向量）和矩阵转置操作，可以变形为[ ch, h*w]和[ h*w, ch]的矩阵。再对两个作内积得到Gram Matrices。 （蓝色条表示每个通道flatten后特征点，最后得到 [ch *ch ]的G矩阵）

2.3 进一步理解

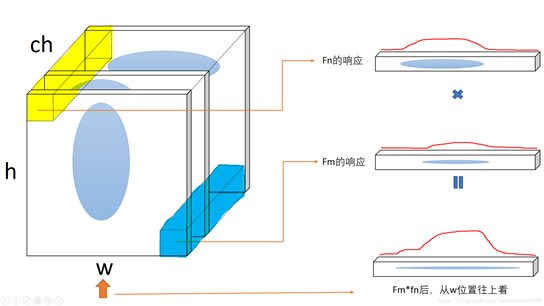
格拉姆矩阵可以看做feature之间的偏心协方差矩阵（即没有减去均值的协方差矩阵），在feature map中，每个数字都来自于一个特定滤波器在特定位置的卷积，因此每个数字代表一个特征的强度，而Gram计算的实际上是两两特征之间的相关性，哪两个特征是同时出现的，哪两个是此消彼长的等等。

格拉姆矩阵用于度量各个维度自己的特性以及各个维度之间的关系。内积之后得到的多尺度矩阵中，对角线元素提供了不同特征图各自的信息，其余元素提供了不同特征图之间的相关信息。这样一个矩阵，既能体现出有哪些特征，又能体现出不同特征间的紧密程度。

关键点：gram矩阵是计算每个通道 i 的feature map与每个通道 j 的feature map的内积。gram matrix的每个值可以说是代表 I 通道的feature map与 j 通道的feature map的互相关程度。

三、Gram matrix的应用-风格迁移

深度学习中经典的风格迁移大体流程是：

1. 准备基准图像和风格图像

2. 使用深层网络分别提取基准图像（加白噪声）和风格图像的特征向量（或者说是特征图feature map）

3. 分别计算两个图像的特征向量的Gram矩阵，以两个图像的Gram矩阵的差异最小化为优化目标，不断调整基准图像，使风格不断接近目标风格图像

关键的一个是在网络中提取的特征图，一般来说浅层网络提取的是局部的细节纹理特征，深层网络提取的是更抽象的轮廓、大小等信息。这些特征总的结合起来表现出来的感觉就是图像的风格，由这些特征向量计算出来的的Gram矩阵，就可以把图像特征之间隐藏的联系提取出来，也就是各个特征之间的相关性高低。

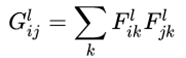
如果两个图像的特征向量的Gram矩阵的差异较小，就可以认定这两个图像风格是相近的。有了表示风格的Gram Matrix，要度量两个图像风格的差异，只需比较他们Gram Matrix的差异即可。

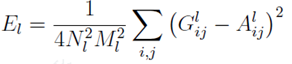
具体可见另一篇文章《风格迁移论文理解--A Neural Algorithm of Artistic Style》展开的介绍。

附件：手写图例辅助理解：