【ML-13-1】隐马尔科夫模型HMM
【ML-13-3】隐马尔科夫模型HMM--Baum-Welch(鲍姆-韦尔奇)
【ML-13-4】隐马尔科夫模型HMM--预测问题Viterbi(维特比)算法
目录
- 基础知识-马尔可夫链
- HMM简介
- HMM定义
- HMM模型的三个基本问题
- 举例
一、基础知识-马尔可夫链
1.1 马尔可夫性质
设{X(t), t ∈ T}是一个随机过程,E为其状态空间,若对于任意的t1<t2< ...<tn<t,任意的x1,x2,...,xn,x∈E,随机变量X(t)在已知变量X(t1)=x1,...,X(tn)=xn之下的条件分布函数只与X(tn)=xn有关,而与X(t1)=x1,...,X(tn-1)=xn-1无关,即条件分布函数满足下列等式,此性质称为马尔可夫性;如果随机过程满足马尔可夫性,则该过程称为马尔可夫过程。
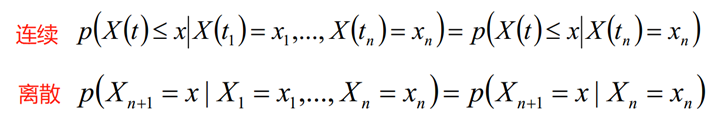
1.2 马尔可夫链
- 马尔可夫链是指具有马尔可夫性质的随机过程。在过程中,在给定当前信息的情况下,过去的信息状态对于预测将来状态是无关的。
- 马尔可夫链在马尔可夫链的每一步,系统根据概率分布,可以从一个状态变成另外一个状态,也可以保持当前状态不变。状态的改变叫做转移,状态改变的相关概率叫做转移概率。
- 马尔可夫链中的三元素是:状态空间S、转移概率矩阵P、初始概率分布π。
1.3 马尔可夫链案例
设将天气状态分为晴、阴、雨三种状态,假定某天的天气状态只和上一天的天气状态有关,状态使用1(晴)、2(阴)、3(雨)表示,转移概率矩阵P如下:
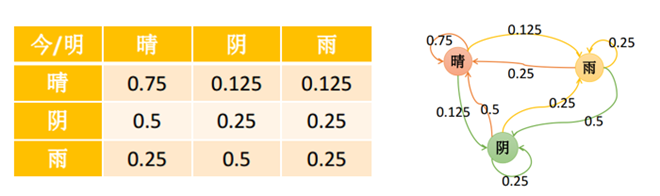
第n+1天天气状态为 j 的概率为:

因此,矩阵P即为条件概率转移矩阵。
矩阵P的第i行元素表示,在上一个状态为i的时候的分布概率,即每行元的和必须为1

最终状态和转移矩阵相关,和初始值无关。
二、HMM简介
隐马尔可夫模型(Hidden Markov Model, HMM)是一种统计模型,在语音识别、行为识别、NLP、故障诊断等领域具有高效的性能。HMM模型时我们的问题一般有这两个特征:
1)我们的问题是基于序列的,比如时间序列,或者状态序列。
2)我们的问题中有两类数据,一类序列数据是可以观测到的,即观测序列;而另一类数据是不能观察到的,即隐藏状态序列,简称状态序列。

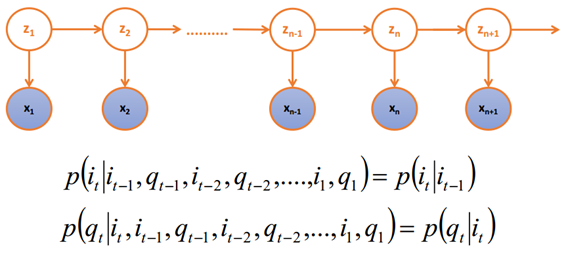
z1,z2...,zn是不可观测的状态,x1,x2,...xn是可观测到的序列;不可观测的状态觉得可观测序列的值(z的取值决定x的取值)。
在z1、z2不可观测的情况下,x1和z2独立吗?x1和x2独立吗?---回答:不独立
在z1给定的情况下,z2和x1是独立的吗? ---回答:独立
三、HMM定义
HMM由隐含状态S、可观测状态O、初始状态概率矩阵π、隐含状态转移概率矩阵A、可观测值转移矩阵B(又称为混淆矩阵,Confusion Matrix);π和A决定了状态序列,B决定观测序列,因此HMM可以使用三元符号表示,称
为HMM的三元素:
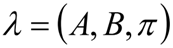
2.1 HMM参数:
- S是所有可能的隐含状态集合;O是所有可能的观测集合:
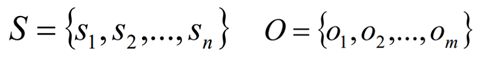
- I是长度为T的状态序列,Q是对应的观测序列:
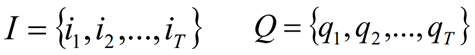
- A是隐含状态转移概率矩阵:

aij是在时刻t处于状态si的条件下时刻t+1转移到状态sj的概率。
- B是可观测值转移概率矩阵:

bij是在时刻t处于状态si的条件下生成观测值oj的概率。
- π是初始状态概率向量:
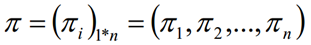

2.2 基本性质:
四、HMM模型的三个基本问题
观测序列概率计算问题:前向-后向算法
给定模型λ=(A,B,π)和观测序列Q={q1,q2,...,qT},计算模型 λ 下观测到序列Q出现的概率P(Q|λ),这个问题是HMM模型三个问题中最简单的,详细请看这个系列的第二篇。
模型学习问题:Baum-Welch(鲍姆-韦尔奇)算法(状态未知)
已知观测序列Q={q1,q2,...,qT},估计模型λ=(A,B,π)的参数,使得在该模型下观测序列P(Q|λ)最大。这个问题的求解需要用到基于EM算法Baum-Welch。是HMM模型三个问题中最复杂的。详细请看这个系列的第三篇。
预测问题也称为解码问题:Viterbi(维特比)算法
给定模型λ=(A,B,π)和观测序列Q={q1,q2,...,qT},求给定观测序列条件概率P(I|Q,λ)最大的隐含状态序列I,这个问题的求解需要用到基于动态规划的维特比算法。详细请看这个系列的第四篇。
五、举例
假设有三个盒子,编号为1,2,3;每个盒子都装有黑白两种颜色的小球,球的比例如下:

按照下列规则的方式进行有放回的抽取小球,得到球颜色的观测序列:
- 按照π的概率选择一个盒子,从盒子中随机抽取出一个小球,记录颜色后,放回盒子中;
- 按照某种条件概率选择新的盒子,重复该操作;
- 最终得到观测序列:"白黑白白黑
- 状态集合:S={盒子1,盒子2,盒子3}
- 观测集合:O={白,黑}
- 状态序列和观测序列的长度T=5
- 初始概率分布π
- 状态转移概率矩阵A(假设)
- 观测概率矩阵B(根据数据而来)
假设状态转移概率矩阵A规则是:如果当前抽球的盒子是第一个盒子,则以0.5的概率仍然留在第一个盒子继续抽球,以0.4的概率去第二个盒子抽球,以0.1的概率去第三个盒子抽球。如果当前抽球的盒子是第二个盒子,则以0.2的概率仍然留在第二个盒子继续抽球,以0.2的概率去第一个盒子抽球,以0.6的概率去第三个盒子抽球。如果当前抽球的盒子是第三个盒子,则以0.3的概率仍然留在第三个盒子继续抽球,以0.2的概率去第一个盒子抽球,以0.5的概率去第二个盒子抽球。如此下去,直到重复五次

在给定参数π、A、B的时候,得到观测序列为"白黑白白黑"的概率是多少?下一节分解
附件一:手写练习


