【ML-12】EM算法和高斯混合模型
目录
- 预备知识
- 简述
- EM算法推导
- EM算法流程
- 收敛性证明
- 应用--高斯混合模型(GMM)
- EM算法优缺点以及应用
一、预备知识
1.1 极大似然函数:
在数理统计学中,似然函数是一种关于统计模型中的参数的函数,表示模型参数中的似然性。"似然性"与"或然性"或"概率"意思相近,都是指某种事件发生的可能性。 多数情况下我们是根据已知条件来推算结果,而最大似然估计是已经知道了结果,然后寻求使该结果出现的可能性最大的条件,以此作为估计值。
求极大似然函数估计值的一般步骤:
- 写出似然函数;
- 对似然函数取对数,并整理;
- 求导数,令导数为0,得到似然方程;--求极大值
- 解似然方程,得到的参数即为所求;
|
↓极大似然估计
|
模型的参数 |
1.2 Jensen不等式
设f是定义域为实数的函数,如果对于所有的实数x,f(x)的二次导数大于等于0,那么f是下凸函数。
Jensen不等式表述如下:如果f是凸函数,X是随机变量,那么:E[f(X)]≥f(E[X]) 。当且仅当X是常量时,上式取等号。其中,E[x]表示x的数学期望。如下图所示:
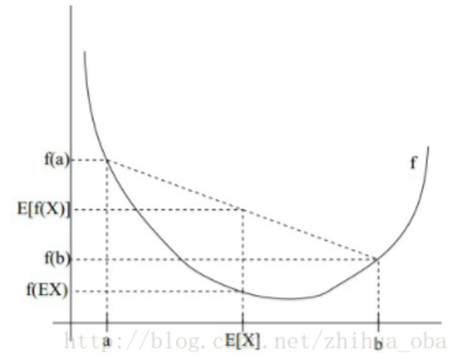
说明:
1、Jensen不等式应用于上凸函数时,不等号方向反向。当且仅当X是常量时,Jensen不等式等号成立。
2、与凸函数(下凸)对比,这里的凹函数(上凸)应有:如果其二阶导数在区间上恒小于等于0,就称为凹函数。如果其二阶导数在区间上恒小于0,就称为严格凹函数。凹凸性不同教材不同说法,本博文直观称之为上凸和下凸。
二、简述
EM算法: Wikipedia的定义:
最大期望算法(Expectation-maximization algorithm,又译为期望最大化算法),是在概率模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐性变量。在HMM模型中鲍姆-韦尔奇算法求解参数的案例中也用到了这种实现。
最大期望算法经过两个步骤交替进行计算:
第一步是计算期望(E),利用对隐藏变量的现有估计值,计算其最大似然估计值;
第二步是最大化(M),最大化在E步上求得的最大似然值来计算参数的值。M步上找到的参数估计值被用于下一个E步计算中,这个过程不断交替进行。
|
↓EM算法
|
给定的m个训练样本{x(1),x(2),...,x(m)},样本间独立,找出样本的模型参数θ,极大化模型分布的对数似然函数如下
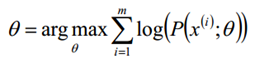
假定样本数据中存在隐含数据z={z(1),z(2),...,z(k)},此时极大化模型分布的对数似然函数如下:
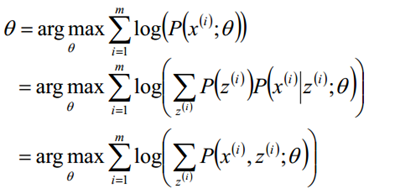
三、EM算法推导
样本集X={x1,…,xm} ,包含m个独立的样本;假定样本数据中存在隐含数据z={z(1),z(2),...,z(k)}我们需要估计概率模型p(x,z)的参数θ,即需要找到适合的θ和z让L(θ)最大。根据上文1.1 极大似然估计中的似然函数取对数所得logL(θ),可以得到如下式:
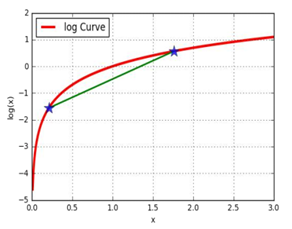
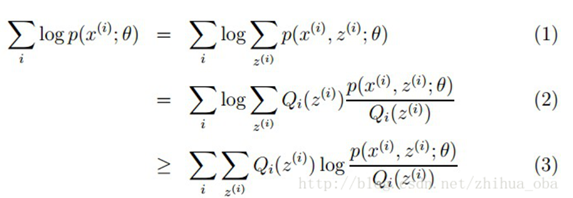
其中,(1)式是根据xi的边缘概率计算得来(z表示隐含的因素),(2)式是由(1)式分子分母同乘一个数得到,(3)式是由(2)式根据Jensen不等式得到(因为对数函数是一个上凸函数,所以f(E[X]) ≥ E[f(X)] )。
式(2)的最大值不是式(3)的最大值啊,而我们想得到式(2)的最大值,那怎么办呢?上面的式(2)和式(3)不等式可以写成:似然函数L(θ) ≥ J(z,Q),我们可以通过不断的最大化这个下界J,来使得L(θ)不断提高,最终达到L(θ)的最大值。
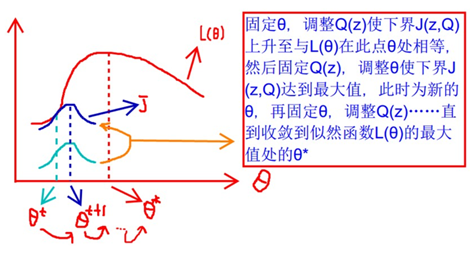
根据Jensen不等式,要想让等式成立,需要让随机变量变成常数值,容易得到以下推导:

上面的是式子中,Q(z,θ)是假设的分布,需要根据Jensen不等式限定条件求出,这里正好等于p(z|x;θ)。
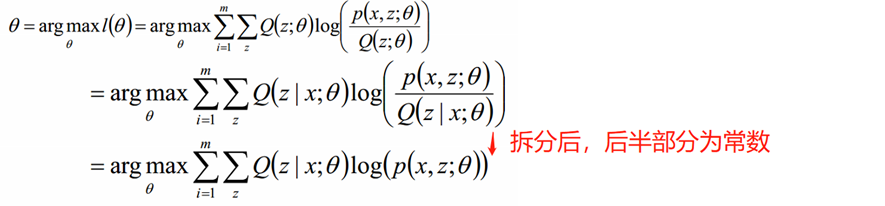
上式子最后一步的Q消除,因为它在迭代之前就已经算出,是一个固定值,不影响最大值的求解。
这就是EM算法的步骤(简而言之:E步就是 定θ,调整Q(z);M步是定Q(z),调整θ)。
四、 EM算法流程
样本数据x={x,x,...,x},联合分布p(x,z;θ),条件分布p(z|x;θ),最大迭代次数J; 重复E、M步骤直到收敛:
1) 随机初始化模型参数θ的初始值θ0
2)开始EM计算:
E步骤:根据参数θ初始值或上一次迭代所得参数值来计算出隐性变量的后验概率(即隐性变量的期望),作为隐性变量的现估计值:
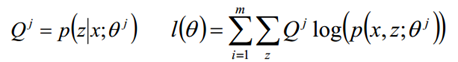
M步骤:将似然函数最大化以获得新的参数值:

就这样,Q(z)求出来代入到θ,θ求出来又反代回Q(z),如此不断的迭代,就可以得到使似然函数L(θ)最大化的参数θ了。
K-means算法和这个非常相似,也是先初始化,再进行迭代求解。
五、收敛性证明
EM算法的收敛性只要我们能够证明对数似然函数的值在迭代的过程中是增加的即可
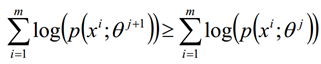
证明如下:
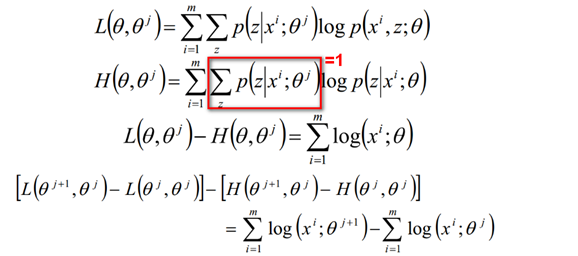

证明了EM算法的收敛性。
六、应用--高斯混合模型
EM算法的一个重要应用场景就是高斯混合模型的参数估计。GMM(Gaussian Mixture Model, 高斯混合模型)是指该算法油多个高斯模型线性叠加混合而成。每个高斯模型称之为component。GMM算法描述的是数据的本身存在的一种分布。
GMM算法常用于聚类应用中,component的个数就可以认为是类别的数量.推导过程和上面一样,知识原来为1个参数,现在变成了2个参数。
假定GMM由k个Gaussian分布线性叠加而成,那么概率密度函数如下:

对数似然函数
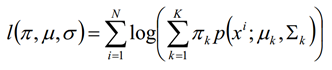
E step:

M step:
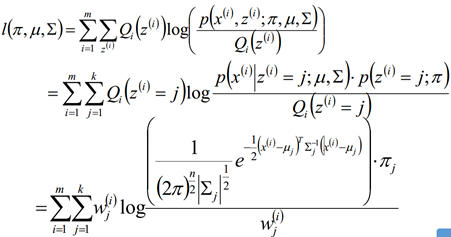
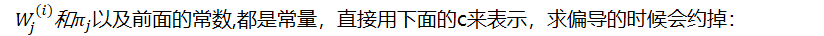
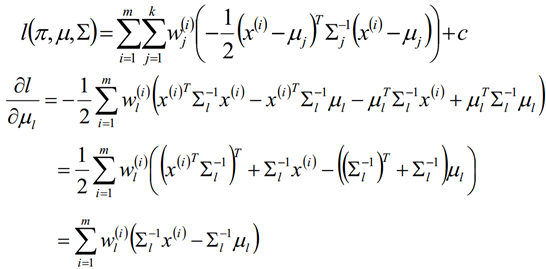
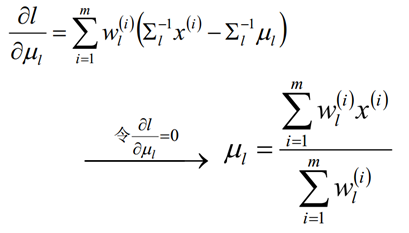
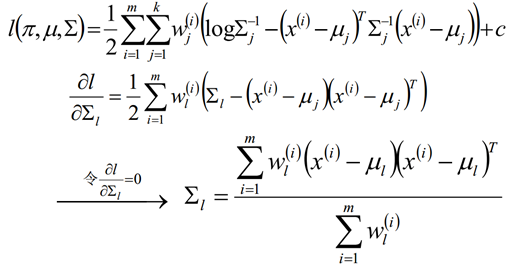
对概率使用拉格朗日乘子法求解
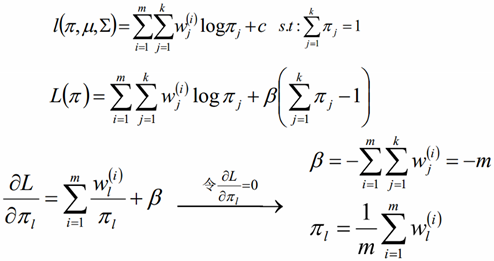
EM算法的其它应用:
k-means算法是EM算法思想的体现,E步骤为聚类过程,M步骤为更新类簇中心。它是一个基础算法,是很多机器学习领域算法的基础,比如隐式马尔科夫算法(HMM), LDA主题模型的变分推断等等。
七、EM算法优缺点
优点:简介中已有介绍,这里不再赘述。
缺点:对初始值敏感:EM算法需要初始化参数θ,而参数θ的选择直接影响收敛效率以及能否得到全局最优解。
附件一、案例分析:

假设现有两个装有不定数量黑球、白球的盒子,随机从盒子中抽取出一个白球的概率分别为p1和p2;为了估计这两个概率,每次选择一个盒子,有放回的连续随机抽取5个球,记录如下:
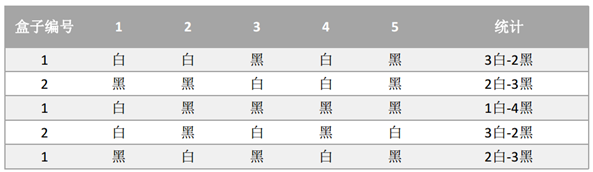
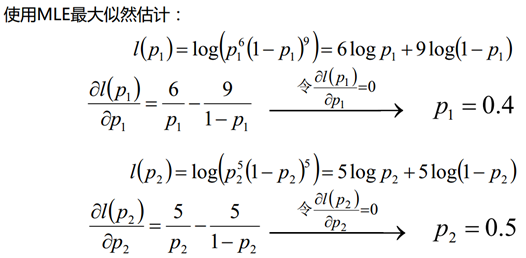
2、当加入了隐形变量时,属于哪个盒子也是未知,如正文中所述的z:
如果现在不知道具体的盒子编号,但是同样还是为了求解p1和p2的值,这个时候就相当于多了一个隐藏变量z, z表示的是每次抽取的时候选择的盒子编号,比如z1就表示第一次抽取的时候选择的是盒子1还是盒子2。
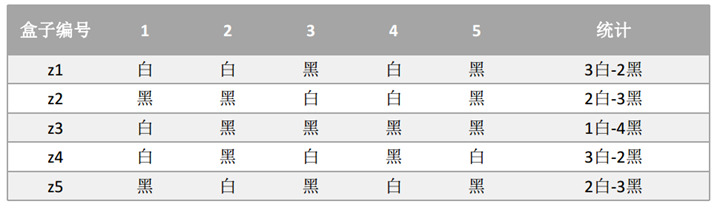
2.1 :随机初始一个概率值:p1=0.1和p2=0.9;然后使用最大似然估计计算每轮操作中从两个盒子中抽取的最大概率。然后计算出来的z值,重新使用极大似然估计法则估计概率值。

上面的L相当于正文中提到的Q。用于估计从哪个盒子中抽取的(计算出各自的概率,如上左表所示)。
再根据预估盒子的概率(大数定律,也就时认为1属于盒子2,这个不严谨,将在2.2进行纠正),反过来计算P1和P2。再进行计算,得到右表所示,发现没有变化,这是算出来的p1和p2不会发生变化。即已经收敛了。
2.2 使用最大似然概率法则估计z和p的值,但是在这个过程中,只使用一个最有可能的值。如果考虑所有的z值,然后对每一组z值都估计一个概率p,那么这个时候估计出来的概率可能会更好,可以用期望的方式来简化这个操作:

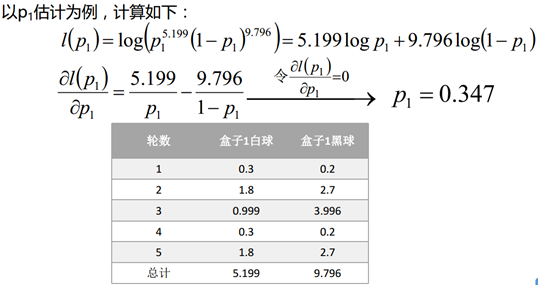
类似方法计算出p2,数据如下,借着计算从每个盒子中抽取的概率:

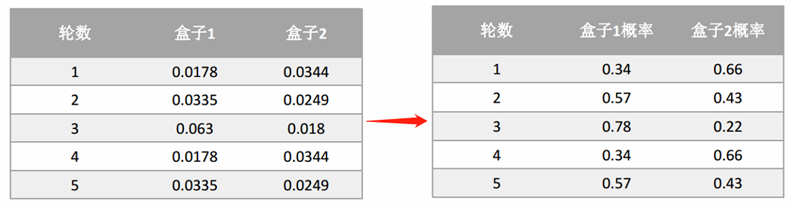
如此循坏,直到p1和p2收敛为止。
附件二、代码
1 # Author:yifan
2 import numpy as np
3 import pandas as pd
4 import matplotlib as mpl
5 import matplotlib.colors
6 import matplotlib.pyplot as plt
7 from sklearn.mixture import GaussianMixture
8 from sklearn.metrics.pairwise import pairwise_distances_argmin
9 # 解决中文显示问题
10 mpl.rcParams['font.sans-serif'] = [u'SimHei']
11 mpl.rcParams['axes.unicode_minus'] = False
12
13 def expand(a, b, rate=0.05):
14 d = (b - a) * rate
15 return a-d, b+d
16 ## 数据加载
17 iris_feature = u'花萼长度', u'花萼宽度', u'花瓣长度', u'花瓣宽度'
18 path = 'datas/iris.data'
19 data = pd.read_csv(path, header=None)
20 x_prime = data[np.arange(4)]
21 y = pd.Categorical(data[4]).codes
22 # 类别数量
23 n_components = 3
24 # 不同特征属性分类
25 feature_pairs = [[0, 1], [0, 2], [0, 3], [1, 2], [1, 3], [2, 3]]
26 plt.figure(figsize=(10, 6), facecolor='w')
27 cm_light = mpl.colors.ListedColormap(['#FFA0A0', '#A0FFA0', '#A0A0FF'])
28 cm_dark = mpl.colors.ListedColormap(['r', 'g', 'b'])
29
30 for k, pair in enumerate(feature_pairs):
31 print(u"特征属性:", iris_feature[pair[0]], iris_feature[pair[1]])
32 x = x_prime[pair]
33 # 计算实际的均值
34 mean = np.array([np.mean(x[y == i], axis=0) for i in range(3)])
35 print(u"实际均值:\n", mean)
36
37 # 模型构建
38 gmm = GaussianMixture(n_components=n_components, covariance_type='full', random_state=28)
39 gmm.fit(x)
40
41 # 效果参数输出
42 print("预测均值=\n", gmm.means_)
43 print("预测方差=\n", gmm.covariances_)
44
45 # 获取预测结果
46 y_hat = gmm.predict(x)
47 order = pairwise_distances_argmin(mean, gmm.means_, axis=1, metric='euclidean')
48 print('顺序:\t', order)
49
50 # 修改预测结果顺序
51 n_sample = y.size
52 n_types = 3
53 change = np.empty((n_types, n_sample), dtype=np.bool)
54 for i in range(n_types):
55 change[i] = y_hat == order[i]
56 for i in range(n_types):
57 y_hat[change[i]] = i
58
59 # 计算准确率
60 acc = u'准确率:%.2f%%' % (100 * np.mean(y_hat == y))
61 print(acc)
62
63 # 画图
64 x1_min, x2_min = x.min()
65 x1_max, x2_max = x.max()
66 x1_min, x1_max = expand(x1_min, x1_max)
67 x2_min, x2_max = expand(x2_min, x2_max)
68 x1, x2 = np.mgrid[x1_min:x1_max:500j, x2_min:x2_max:500j]
69 grid_test = np.stack((x1.flat, x2.flat), axis=1)
70 grid_hat = gmm.predict(grid_test)
71
72 change = np.empty((n_types, grid_hat.size), dtype=np.bool)
73 for i in range(n_types):
74 change[i] = grid_hat == order[i]
75 for i in range(n_types):
76 grid_hat[change[i]] = i
77 grid_hat = grid_hat.reshape(x1.shape)
78
79 # 子图
80 plt.subplot(3, 2, k + 1)
81 plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light)
82 plt.scatter(x[pair[0]], x[pair[1]], s=30, c=y, marker='o', cmap=cm_dark, edgecolors='k')
83 xx = 0.9 * x1_min + 0.1 * x1_max
84 yy = 0.2 * x2_min + 0.8 * x2_max
85 plt.text(xx, yy, acc, fontsize=14)
86 plt.xlim((x1_min, x1_max))
87 plt.ylim((x2_min, x2_max))
88 plt.xlabel(iris_feature[pair[0]], fontsize=14)
89 plt.ylabel(iris_feature[pair[1]], fontsize=14)
90 plt.grid()
91 print()
92 print()
93
94 plt.tight_layout(2)
95 plt.suptitle(u'EM算法鸢尾花数据分类', fontsize=20)
96 plt.subplots_adjust(top=0.90)
97 plt.show()
结果:
参考博文:
https://www.cnblogs.com/pinard/p/6912636.html
https://blog.csdn.net/v_july_v/article/details/81708386
附件三:手写练习



