图像分割简介
目录
- 意义
- 图像分割方法
- 评价方法:最终测量精度UMA
一、意义
概念:
- 把图像分解成构成它的部件和对象的过程
- 定位感兴趣对象在图像中的位置和范围
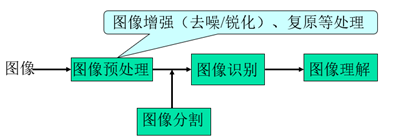
意义:图像分割是图像处理与理解、模式识别和人工智能等多个领域中一个十分重要且又十分困难的问题,是计算机视觉技术中关键步骤,如下图所示。图像分割应用在许多方面。应用:汽车车型自动识别系统、检查癌细胞、精密零件表面缺陷检测,处理卫星拍摄的地形地貌照片等。在所有这些应用领域中,最终结果很大程度上依赖于图像分割的结果。
图像分割的数学定义:
令集合I代表整个图像区域,H表示具有相同性质的谓词,Ri表示I分解的n个区域,i=1,2…n,则图像分割区域满足下列条件:
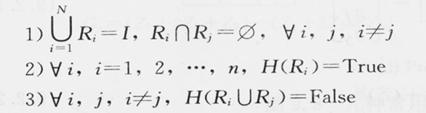
对应文字说明:
1) 表明分割区域要覆盖整个图像且各区域互不重叠;
2) 表明每一个区域都具有相同的性质;
3) 表明两个区域性质相异不能合并为一个区域。
总之:图像分割的任务是把图像分离成互不交叠的有相同性质的区域。
二、图像分割方法
2.1 基于边缘的分割方法
先提取区域边界,再确定边界限定的区域;涉及到边缘检测核边缘连接两个部分。基本思想:先检测图像中的边缘点再按一定策略链接成轮廓,从而构成分割区域。
2.1.1 边缘检测
边缘检测的意义:边界存在于目标与背景、目标与目标、区域与区域之间,是图像最基本的特征,包含了在实际应用中用于分割的基本信息。人物体时,首先感觉到的便是边缘。
边缘检测的对象:检测灰度级或者结构具有突变的地方,这种灰度或者结构不连续性称为边缘。
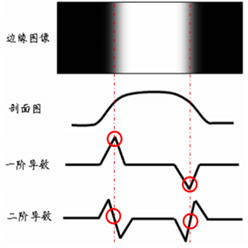
边缘检测处理方法:图像中相邻的不同区域间总存在边缘,边缘处像素的灰度值不连续,这种不连续性可通过求导数来检测到,因此常用灰度的一阶或二阶微分算子进行边缘检测。直观理解如下图所示,一阶导数的峰值,二阶导数的零点值。
2.1.2 边缘连接
意义:利用前述的方法可以检测出边缘点,但由于噪音等原因,边界的特征很少能够被完整地描述,获得边缘点有可能是不连续的,在亮度不一致的地方会中断。因此典型的边界检测算法后面总要跟随着连接过程和其它边界检测过程,用来归整边界像素,将边缘像素组合成有意义的边缘信息。本文介绍局部处理法进行。另外还有Hough变换,暂时不介绍
局部处理法:比较梯度算子的响应强度和梯度方向确定两个点是否同属一条边,分析图像中每个点(x,y)的一个领域,根据梯度确定边缘像素的相似性。
强度:对于点(x',y'),判断其是否与邻域内的边界点(x,y)相似,其中T是一个非负的阈值。

方向:对于点(x',y'),判断其是否与邻域内的边界点(x,y)的方向角相似,其中A是一个角度阈值
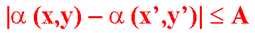
如果强度和方向准则得到满足,则 (x,y)邻域中的点就与位于(x,y)的像素连接起来。
边缘检测缺陷:需要指出的是,边缘并不等同于实际目标的边界。
1、图像数据是二、三维的,而实际物体是N维的,从高维到低维的投影必然会造成信息的丢失;
2、成像过程中的光照不均和噪声等因素的影响,使得有边界的地方不一定能检测出边缘,检测出有边缘的地方也不一定代表实际边界。
基于边缘检测的图像分割方法虽然简单,理论和方法仍存在有待解决的地方。
2.2 基于区域的分割方法
确定每个像素的归属区域,从而完成分割;阈值分割法(本文介绍)、区域生长法和分裂合并法等。
阈值分割法
基本原理:通过设定不同的特征阈值,把图像像素点分为若干类
- 确定一个灰度阈值
- 将灰度值大于给定阈值的像元判归为某一个物体,赋予同一个编号
- 将灰度值小于给定阈值的像元统一判归为另一类物体,赋于另外一个编号。
适用:要分割的物体与图像的背景有较强对比度的图像。被分割的物体内部灰度值比较均一且它周围的背景灰度值也比较均一,该法效果比较理想。
关键:如何找到合适的阈值。
简单直方图分割法:60年代中期,Prewitt提出了直方图双峰法,即如果灰度级直方图呈明显的双峰状,则选取两峰之间的谷底所对应的灰度级作为阈值。

直方图阈值分割法可用数学表达式来描述。设图像f(i, j),其灰度级范围为[z1, z2],设T为阈值,是z1和z2内任一值,可得一幅二值图像,其数学表达式为:
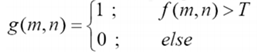
迭代式阈值选择
基本思想:初始时选择一个阈值作为初始估计值,然后按照某种策略不断地改进这一估计值,直到满足给定的准则为止。
算法实例:
1)选择图像灰度的中值作为初始阈值T0
2)利用阈值T把图像分割成两个区域R1和R2,分别计算R1和R2的灰度均值
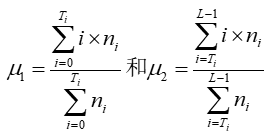
3)计算出新的阈值Ti+1:
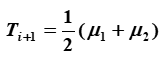
4)重复步骤2~3,直到Ti+1和Ti的差小于某个给定值。
三、评价方法:最终测量精度UMA
分割的目的是将感兴趣的目标分离出来,因此,通过对原始目标特征值和分割出的目标特征值进行精确测量,根据结果来评价分割方法的优劣是常用的方法。
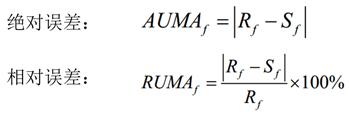
Rf代表从作为参考图像中获得的原始特征值;Sf代表从分割图像中获得的实际特征量值,例如:重心、面积、长短轴之比等。


