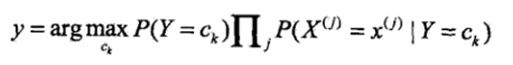【ML-11】朴素贝叶斯算法
目录
- 贝叶斯法的定义
- 后验概率最大化--贝叶斯的理论基础
- 朴素贝叶斯的参数估计
- 贝叶斯估计
- 其它贝叶斯公式
- 朴素贝叶斯总结
朴素贝叶斯很直观,计算量也不大,在很多领域有广泛的应用,主要工程中应用为文本分词分类一块,这里我们就对朴素贝叶斯算法原理做一个小结:
一、贝叶斯法的定义
1.1 贝叶斯基本公式
- 先验概率P(A):在不考虑任何情况下,A事件发生的概率
- 条件概率P(B|A):A事件发生的情况下,B事件发生的概率

- 后验概率P(A|B):在B事件发生之后,对A事件发生的概率的重新评估
- 联合概率:联合概率指的是包含多个条件且所有条件同时成立的概率,记作P(X=a,Y=b)或P(a,b),有的书上也习惯记作P(ab).
- 全概率:如果A和A'构成样本空间的一个划分,那么事件B的概率为:A和A'的概率分别乘以B对这两个事件的概率之和。

- 基于条件概率的贝叶斯定律公式

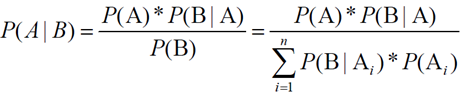
1.2 朴素贝叶斯算法
可以理解为求解过程的变化,等式左侧公式较难直接求解,可以通过转换成右侧形式。
对于给定的数据集。
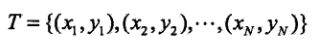
假定输出的类别yi ∈ {c1, c2, ...., ck},朴素贝叶斯通过训练数据集的条件概率分布P(x|y)来学习联合概率。因此在这里我们近似的求先验概率分布和条件概率分布来替代它。
先验概率分布如下(先验概率的求解:可以根据大数定理认为就是该类别在总体样本中的比例)
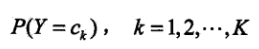
条件概率分布如下
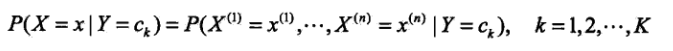
朴素贝叶斯法假定上面的条件概率中各特征之间是相互独立的。此时我们可以做链式展开,表达式如下
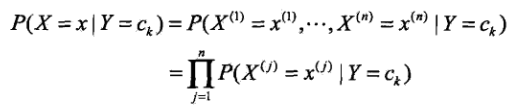
朴素贝叶斯法实际上是有求联合概率分布的过程,以及通过联合概率求后验概率(也是一种条件概率)的过程,像这类的分类器属于生成式模型。区别于它的就是判别生成式模型,常见的有决策树,逻辑回归,SVM等,这类模型都是直接生成结果(可能是P(y) 或者P(y|x) )。而贝叶斯是要先计算p(x,y)的,了解了先验概率和条件概率的计算过程,使用贝叶斯定理计算后验概率的

引入朴素的思想,假设各特征之间相互独立。(以上两式结合得到下式)
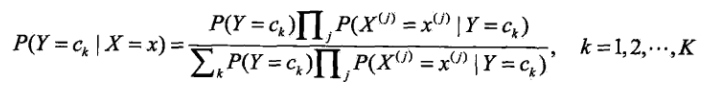
这就是朴素贝叶斯分类的基本公式,因此我们的模型可以建为
|
而对于右边式子中的分母,分母是一个和类别无关的式子,也就是说对于所有的ck都是一样的,然后在这里我们只是求的最大概率的类别,因此去掉这一项是不会影响结果的(即对表达式进行同比例的放大或缩小是不会影响最大解的判断的),最终的式子可以写成
|
二、后验概率最大化--贝叶斯的理论基础
先来了解下0-1损失函数:
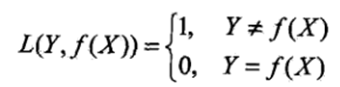
此时的期望风险函数,在优化模型的时候我们的目的是为了使得期望损失最小化:
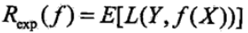
而对于朴素贝叶斯模型,期望损失函数可以表示为:

这里面的损失函数和0-1损失有所不同,可以看成分类到每个类别的概率乘以0-1损失函数,也就是说在k中只有一次L函数会取0,其余的都取1,此时我们还要使得取0时的条件概率P(ck|x)是最大的,这样整体的期望损失就是最小的。具体的数学推导过程如下:

为了使得期望风险最小化就是使得后验概率最大化:
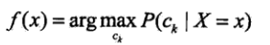
也解释了一中为啥要求max值
三、朴素贝叶斯的参数估计
具体步骤:
3.1 计算先验概念和条件概率:
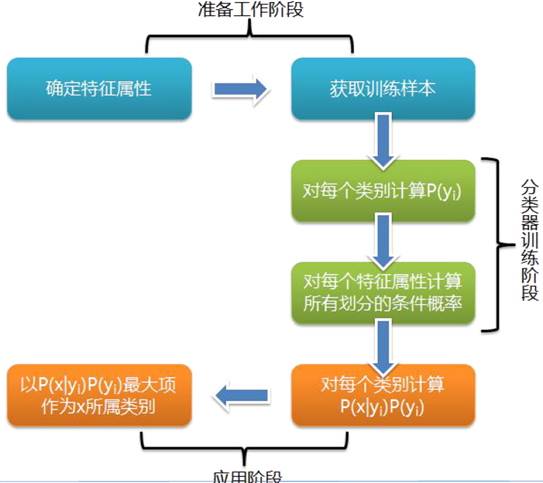
采用极大似然估计来求解先验概率和条件概率,先验概率的极大似然估计(分子为yi=Ck的个数):
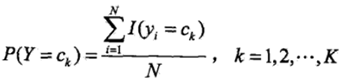
条件概率的极大似然估计

3.2:计算各实例的概率:

3.3:确定分类:
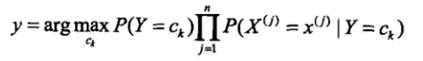
即根据3.2,取概率最大的对应的Y值即可。
但是用极大似然估计可能会出现概率值为0的情况。这时候会影响到后验概率的计算(因为链式求解时,一旦存在某一个值为0,则会导致整个链式的解为0,也就是求得的条件概率为0),因此我们对上述公式进行改进,即为以下形式。
四、贝叶斯估计
先验概率的表达式
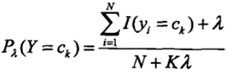
贝叶斯估计的条件概率表达式
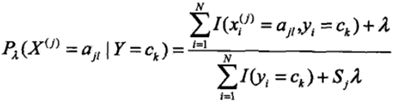

五、其它贝叶斯公式
5.1 高斯朴素贝叶斯
Gaussian Naive Bayes是指当特征属性为连续值时,而且分布服从高斯分布,那么在计算P(x|y)的时候可以直接使用高斯分布的概率公式:

因此只需要计算出各个类别中此特征项划分的各个均值和标准差

5.2 伯努利朴素贝叶斯
Bernoulli Naive Bayes是指当特征属性为连续值时,而且分布服从伯努利分布,那么在计算P(x|y)的时候可以直接使用伯努利分布的概率公式:
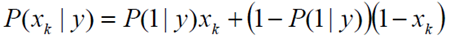
伯努利分布是一种离散分布,只有两种可能的结果。1表示成功,出现的概率为p;0表示失败,出现的概率为q=1-p;其中均值为E(x)=p,方差为Var(X)=p(1-p)
5.3 多项式朴素贝叶斯
Multinomial Naive Bayes是指当特征属性服从多项分布(用于数据离散较多),从而,对于每个类别y,参数为θy=(θy1,θy2,...,θyn),其中n为特征属性数目,那么P(xi|y)的概率为θyi。
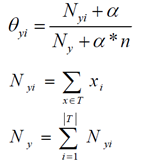
六、朴素贝叶斯总结
优点:
1)朴素贝叶斯模型分类效率稳定
2)对小规模的数据集表现很好,能处理多分类问题,适合增量式训练,尤其是数据集超出内存后,我们可以一批批的去训练
3)对缺失数据不太敏感,算法比较简单,常用于文本分类
缺点;
1)理论上,朴素贝叶斯较其他模型相比具有最小的误差率,但实际上却不一定,因为朴素贝叶斯引进了各特征之间相互独立这一假设。因此在各特征之间相关性较强时,朴素贝叶斯表现一般,但是在各特征之间独立性很强时,朴素贝叶斯表现很好
2)通过先验和数据来决定后验的概率从而决定分类,所以分类决策存在一定的错误率
3)对输入数据的表达形式很敏感
附件一:公式理解的例题

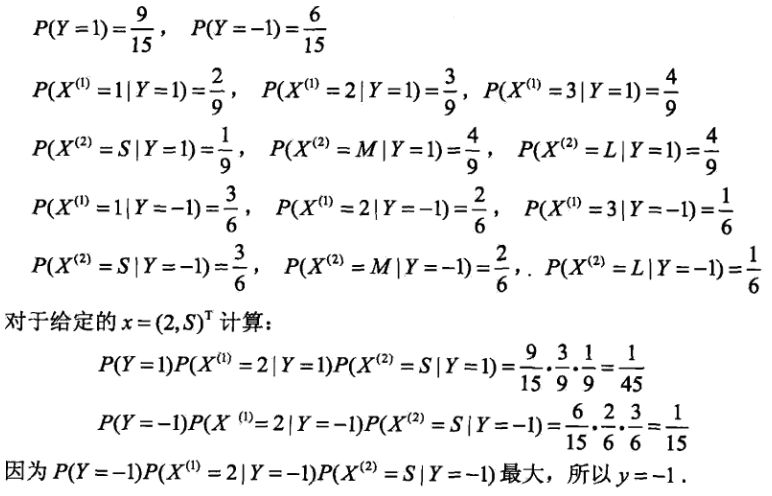
贝叶斯估计引入平滑计算:

附件二:贝叶斯算法案例一:鸢尾花数据分类
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 | # Author:yifan import numpy as np import pandas as pd import matplotlib.pyplot as plt import matplotlib as mpl from sklearn.preprocessing import StandardScaler, MinMaxScaler, PolynomialFeatures from sklearn.naive_bayes import GaussianNB, MultinomialNB #高斯贝叶斯和多项式朴素贝叶斯 from sklearn.pipeline import Pipeline from sklearn.metrics import accuracy_score from sklearn.model_selection import train_test_split from sklearn.neighbors import KNeighborsClassifier ## 设置属性防止中文乱码 mpl.rcParams['font.sans-serif'] = [u'SimHei'] mpl.rcParams['axes.unicode_minus'] = False # 花萼长度、花萼宽度,花瓣长度,花瓣宽度 iris_feature_E = 'sepal length', 'sepal width', 'petal length', 'petal width' iris_feature_C = u'花萼长度', u'花萼宽度', u'花瓣长度', u'花瓣宽度' iris_class = 'Iris-setosa', 'Iris-versicolor', 'Iris-virginica' features = [2,3] ## 读取数据 path = './datas/iris.data' # 数据文件路径 data = pd.read_csv(path, header=None) x = data[list(range(4))] x = x[features] y = pd.Categorical(data[4]).codes ## 直接将数据特征转换为0,1,2 print ("总样本数目:%d;特征属性数目:%d" % x.shape) ## 0. 数据分割,形成模型训练数据和测试数据。训练数据集样本数目:120, 测试数据集样本数目:30 x_train1, x_test1, y_train1, y_test1 = train_test_split(x, y, train_size=0.8, random_state=14) x_train, x_test, y_train, y_test = x_train1, x_test1, y_train1, y_test1 ## 高斯贝叶斯模型构建 clf = Pipeline([ ('sc', StandardScaler()),#标准化,把它转化成了高斯分布 ('poly', PolynomialFeatures(degree=4)), ('clf', GaussianNB())]) # MultinomialNB多项式贝叶斯算法中要求特征属性的取值不能为负数 ## 训练模型 clf.fit(x_train, y_train) ## 计算预测值并计算准确率 y_train_hat = clf.predict(x_train) print ('训练集准确度: %.2f%%' % (100 * accuracy_score(y_train, y_train_hat))) y_test_hat = clf.predict(x_test) print ('测试集准确度:%.2f%%' % (100 * accuracy_score(y_test, y_test_hat))) ## 产生区域图 N, M = 500, 500 # 横纵各采样多少个值 x1_min1, x2_min1 = x_train.min() x1_max1, x2_max1 = x_train.max() x1_min2, x2_min2 = x_test.min() x1_max2, x2_max2 = x_test.max() x1_min = np.min((x1_min1, x1_min2)) x1_max = np.max((x1_max1, x1_max2)) x2_min = np.min((x2_min1, x2_min2)) x2_max = np.max((x2_max1, x2_max2))
t1 = np.linspace(x1_min, x1_max, N) t2 = np.linspace(x2_min, x2_max, N) x1, x2 = np.meshgrid(t1, t2) # 生成网格采样点 x_show = np.dstack((x1.flat, x2.flat))[0] # 测试点
cm_light = mpl.colors.ListedColormap(['#77E0A0', '#FF8080', '#A0A0FF']) cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b']) y_show_hat = clf.predict(x_show) # 预测值 y_show_hat = y_show_hat.reshape(x1.shape)
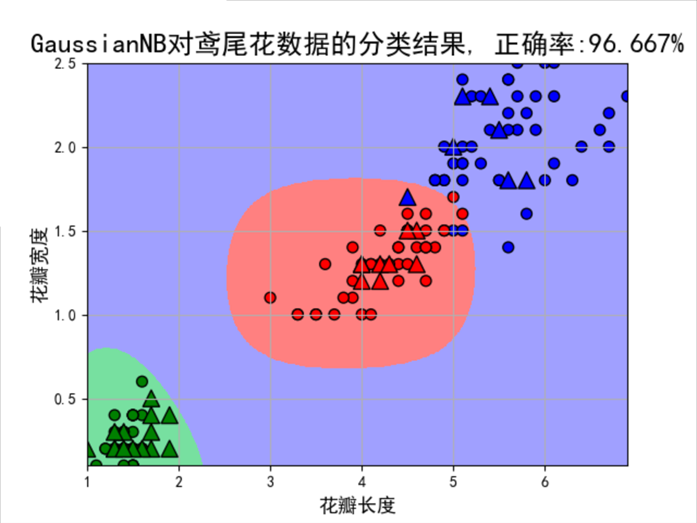
## 画图 plt.figure(facecolor='w') plt.pcolormesh(x1, x2, y_show_hat, cmap=cm_light) # 预测值的显示,显示区域范围 plt.scatter(x_train[features[0]], x_train[features[1]], c=y_train, edgecolors='k', s=50, cmap=cm_dark) plt.scatter(x_test[features[0]], x_test[features[1]], c=y_test, marker='^', edgecolors='k', s=120, cmap=cm_dark) plt.xlabel(iris_feature_C[features[0]], fontsize=13) plt.ylabel(iris_feature_C[features[1]], fontsize=13) plt.xlim(x1_min, x1_max) plt.ylim(x2_min, x2_max) plt.title(u'GaussianNB对鸢尾花数据的分类结果, 正确率:%.3f%%' % (100 * accuracy_score(y_test, y_test_hat)), fontsize=18) plt.grid(True) plt.show() |
结果:
训练集准确度: 96.67%
测试集准确度:96.67%
附件三:手写练习