【ML-7-应用】聚类算法-时间序列聚类(DTW和LB_Keogh距离)
目录
- 问题分析
- 数据处理
- 代码实现
- 结果
今天兄弟找我帮忙:希望基于白细胞数据把新型肺炎患者的数据做一个聚类并画出大体曲线:也就是将相同变化的曲线进行分类并拟合。定位此问题为无监督的分类问题。因此想到了聚类的方法。
一、问题分析
1、首先尝试了使用:提取时间序列的统计学特征值,例如最大值,最小值等。然后利目前常用的算法根据提取的特征进行分类,例如Naive Bayes, SVMs,KNN 等。发现效果并不是很好。
2、尝试基于K-means的无监督形式分类,这种分类方式基于两个数据的距离进行分类,这样要定义号距离的概念,后来查阅资料,考虑使用动态时间规整(Dynamic Time Warping, DTW)。下文主要基于这方面进行展开。
二、数据处理
给出的数据较为完整,就一个excel表格,做了以下简单的排序,原始数据可见文末github地址。
三、代码实现
3.1 动态时间规整(Dynamic Time Warping, DTW)
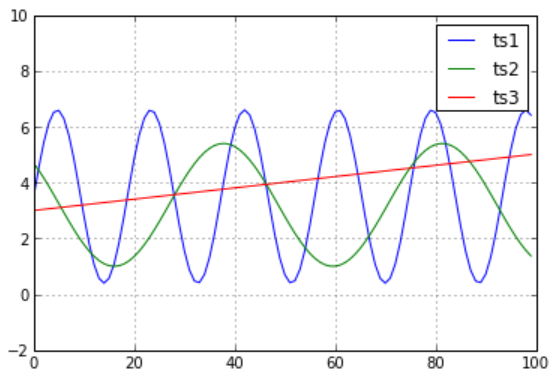
如果是欧拉距离:则ts3比ts2更接近ts1,但是肉眼看并非如此。故引出DTW距离。
动态时间规整算法,故名思议,就是把两个代表同一个类型的事物的不同长度序列进行时间上的"对齐"。比如DTW最常用的地方,语音识别中,同一个字母,由不同人发音,长短肯定不一样,把声音记录下来以后,它的信号肯定是很相似的,只是在时间上不太对整齐而已。所以我们需要用一个函数拉长或者缩短其中一个信号,使得它们之间的误差达到最小。下面这篇博文给了比较好的解释:https://blog.csdn.net/lin_limin/article/details/81241058。 简单英文解释如下(简而言之:就是允许错开求差值,并且取最小的那个作为距离。)

DTW距离代码定义如下:
1 def DTWDistance(s1, s2):
2 DTW={}
3 for i in range(len(s1)):
4 DTW[(i, -1)] = float('inf')
5 for i in range(len(s2)):
6 DTW[(-1, i)] = float('inf')
7 DTW[(-1, -1)] = 0
8 for i in range(len(s1)):
9 for j in range(len(s2)):
10 dist= (s1[i]-s2[j])**2
11 DTW[(i, j)] = dist + min(DTW[(i-1, j)],DTW[(i, j-1)], DTW[(i-1, j-1)])
12
13 return math.sqrt(DTW[len(s1)-1, len(s2)-1])
14
15
这样求解相对较为麻烦,时间复杂度比较高,故做了一个小的加速:
#DTW距离,只检测前W个窗口的值,定义错开的部分W,减少递归寻找量
1 def DTWDistance(s1, s2, w):
2 DTW = {}
3 w = max(w, abs(len(s1) - len(s2)))
4 for i in range(-1, len(s1)):
5 for j in range(-1, len(s2)):
6 DTW[(i, j)] = float('inf')
7 DTW[(-1, -1)] = 0
8 for i in range(len(s1)):
9 for j in range(max(0, i - w), min(len(s2), i + w)):
10 dist = (s1[i] - s2[j]) ** 2
11 DTW[(i, j)] = dist + min(DTW[(i - 1, j)], DTW[(i, j - 1)], DTW[(i - 1, j - 1)])
12 return math.sqrt(DTW[len(s1) - 1, len(s2) - 1])
3.2 LB_Keogh距离
主要思想是在搜索数据很大的时候, 逐个用DTW算法比较每一条是否匹配非常耗时。那我们能不能使用一种计算较快的近似方法计算LB, 通过LB处理掉大部分不可能是最优匹配序列的序列,对于剩下的序列在使用DTW逐个比较呢?英文解释如下:

中文解释如下,主要参考其它博文:LB_keogh的定义相对复杂,包括两部分。
第一部分为Q的{U, L} 包络曲线(具体如图), 给Q序列的每个时间步定义上下界。 定义如下

其中 r 是一段滑行窗距离,可以自定义。
示意图如下:
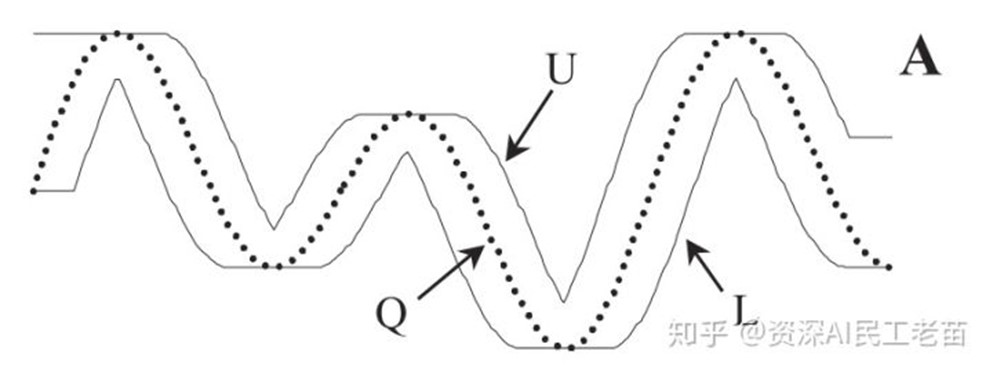
U 为上包络线,就是把每个时间步为Q当前时间步前后r的范围内最大的数。L 下包络线同理。那么LB_Keogh定义如下:
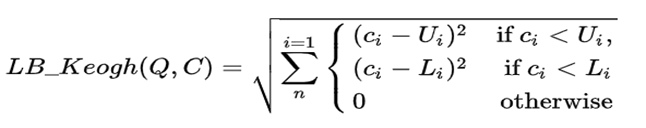
用图像描述如下:

1 def LB_Keogh(s1, s2, r):
2 LB_sum = 0
3 for ind, i in enumerate(s1):
4 # print(s2)
5 lower_bound = min(s2[(ind - r if ind - r >= 0 else 0):(ind + r)])
6 upper_bound = max(s2[(ind - r if ind - r >= 0 else 0):(ind + r)])
7 if i >= upper_bound:
8 LB_sum = LB_sum + (i - upper_bound) ** 2
9 elif i < lower_bound:
10 LB_sum = LB_sum + (i - lower_bound) ** 2
11 return math.sqrt(LB_sum)
3.3 使用k-means算法实现聚类
1 #3 定义K-means算法
2 #num_clust分类的数量,
3 def k_means_clust(data, num_clust, num_iter, w=3):
4 ## 步骤一: 初始化均值点
5 centroids = random.sample(list(data), num_clust)
6 counter = 0
7 for n in range(num_iter):
8 counter += 1
9 # print
10 # counter
11 assignments = {} #存储类别0,1,2等类号和所包含的类的号码
12 # 遍历每一个样本点 i ,因为本题与之前有所不同,多了ind的编码
13 for ind, i in enumerate(data):
14 min_dist = float('inf') #最近距离,初始定一个较大的值
15 closest_clust = None # closest_clust:最近的均值点编号
16 ## 步骤二: 寻找最近的均值点
17 for c_ind, j in enumerate(centroids): #每个点和中心点的距离,共有num_clust个值
18 if LB_Keogh(i, j, 3) < min_dist: #循环去找最小的那个
19 cur_dist = DTWDistance(i, j, w)
20 if cur_dist < min_dist: #找到了ind点距离c_ind最近
21 min_dist = cur_dist
22 closest_clust = c_ind
23 ## 步骤三: 更新 ind 所属簇
24 # print(closest_clust)
25 if closest_clust in assignments:
26 assignments[closest_clust].append(ind)
27 else:
28 assignments[closest_clust] = []
29 assignments[closest_clust].append(ind)
30 # recalculate centroids of clusters ## 步骤四: 更新簇的均值点
31 for key in assignments:
32 clust_sum = 0
33 for k in assignments[key]:
34 clust_sum = clust_sum + data[k]
35 centroids[key] = [m / len(assignments[key]) for m in clust_sum]
36 return centroids,assignments #返回聚类中心值,和聚类的所有点的数组序号
3.4 根据聚类打印出具体分类情况:
1 num_clust = 2 #定义需要分类的数量
2 centroids,assignments = k_means_clust(WBCData, num_clust,800, 3)
3 for i in range(num_clust):
4 s = []
5 WBC01 = []
6 days01 = []
7 for j, indj in enumerate(assignments[i]): #画出各分类点的坐标
8 s.append(int(Numb[indj*30]))
9 WBC01 = np.hstack((WBC01,WBC[30 * indj:30 * indj + 30]))
10 days01 = np.hstack((days01 , days[0: 30]))
11 print(s)
12 plt.title('%s' % s)
13 plt.plot(centroids[i],c="r",lw=4)
14 plt.scatter(days01, WBC01 )
15 plt.show()
四、结果
定义了分成两类的情形,可以根据num_clust 的值进行灵活的调整,等于2是的分类和图示情况如下:
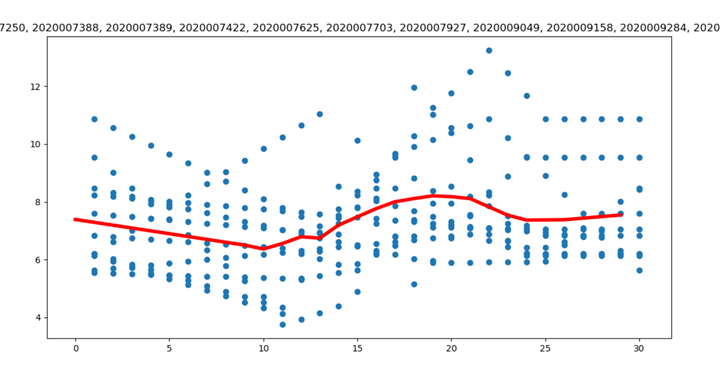
WBC01:[6774, 7193, 8070, 8108, 8195, 2020006799, 2020007003, 2020007251, 2020007420, 2020007636, 2020007718, 2020007928, 2020007934, 2020008022, 2020008196, 2020008239, ……] 不全部列出
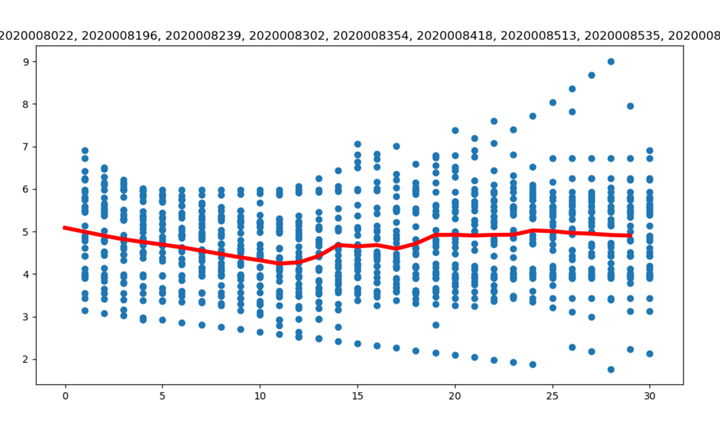
WBC02:[2020007250, 2020007388, 2020007389, 2020007422, 2020007625, 2020007703, 2020007927 , ……]
说明:
代码训练过程中,一定要注意数据类型,比如matrix和ndarray,虽然打印的时候都是(45,30),但是再训练的时候,稍加不注意,就会导致乱七八糟的问题,需要打印排查好久。
本文的数据和代码,请登录:my github ,进行下载。若是对您有用,请不吝给颗星。
附件一:整体代码
1 # Author:yifan
2
3 import pandas as pd
4 import numpy as np
5 import matplotlib.pylab as plt
6 import math
7 import random
8 import xlrd
9 import numpy as np
10 import sys
11
12
13 #演示
14 # import pandas as pd
15 # import numpy as np
16 # import matplotlib.pylab as plt
17 # x=np.linspace(0,50,100)
18 # ts1=pd.Series(3.1*np.sin(x/1.5)+3.5)
19 # ts2=pd.Series(2.2*np.sin(x/3.5+2.4)+3.2)
20 # ts3=pd.Series(0.04*x+3.0)
21 # ts1.plot()
22 # ts2.plot()
23 # ts3.plot()
24 # plt.ylim(-2,10)
25 # plt.legend(['ts1','ts2','ts3'])
26 # plt.show()
27 # def euclid_dist(t1,t2):
28 # return math.sqrt(sum((t1-t2)**2))
29 # print (euclid_dist(ts1,ts2)) #26.959216038
30 # print (euclid_dist(ts1,ts3)) #23.1892491903
31
32
33 #1 数据提取
34 # workbook = xlrd.open_workbook(r"D:\datatest\xinguanfeiyan\20200229.xlsx")
35 workbook = xlrd.open_workbook(r"D:\datatest\xinguanfeiyan\20200315L.xlsx")
36 worksheet = workbook.sheet_by_index(0)
37 n = worksheet.nrows
38 days = [0]*(n-1)
39 WBC = [0]*(n-1)
40 Numb = [0]*(n-1)
41 for i in range(1,n):
42 Numb[i-1] = worksheet.cell_value(i,0)
43 days[i-1] = worksheet.cell_value(i,1)
44 WBC[i-1] = worksheet.cell_value(i,2)
45 s=int(len(WBC)/30)
46 WBCData = np.mat(WBC).reshape(s,30)
47 WBCData = np.array(WBCData)
48 # print(WBCData)
49
50 #2 定义相似距离
51 #DTW距离,时间复杂度为两个时间序列长度相乘
52 def DTWDistance(s1, s2):
53 DTW = {}
54 for i in range(len(s1)):
55 DTW[(i, -1)] = float('inf')
56 for i in range(len(s2)):
57 DTW[(-1, i)] = float('inf')
58 DTW[(-1, -1)] = 0
59 for i in range(len(s1)):
60 for j in range(len(s2)):
61 dist = (s1[i] - s2[j]) ** 2
62 DTW[(i, j)] = dist + min(DTW[(i - 1, j)], DTW[(i, j - 1)], DTW[(i - 1, j - 1)])
63 return math.sqrt(DTW[len(s1) - 1, len(s2) - 1])
64
65 #DTW距离,只检测前W个窗口的值,减少时间复杂度
66 def DTWDistance(s1, s2, w):
67 DTW = {}
68 w = max(w, abs(len(s1) - len(s2)))
69 for i in range(-1, len(s1)):
70 for j in range(-1, len(s2)):
71 DTW[(i, j)] = float('inf')
72 DTW[(-1, -1)] = 0
73 for i in range(len(s1)):
74 for j in range(max(0, i - w), min(len(s2), i + w)):
75 dist = (s1[i] - s2[j]) ** 2
76 DTW[(i, j)] = dist + min(DTW[(i - 1, j)], DTW[(i, j - 1)], DTW[(i - 1, j - 1)])
77 return math.sqrt(DTW[len(s1) - 1, len(s2) - 1])
78 #Another way to speed things up is to use the LB Keogh lower bound of dynamic time warping
79 def LB_Keogh(s1, s2, r):
80 LB_sum = 0
81 for ind, i in enumerate(s1):
82 # print(s2)
83 lower_bound = min(s2[(ind - r if ind - r >= 0 else 0):(ind + r)])
84 upper_bound = max(s2[(ind - r if ind - r >= 0 else 0):(ind + r)])
85 if i >= upper_bound:
86 LB_sum = LB_sum + (i - upper_bound) ** 2
87 elif i < lower_bound:
88 LB_sum = LB_sum + (i - lower_bound) ** 2
89 return math.sqrt(LB_sum)
90
91
92 #3 定义K-means算法
93 #num_clust分类的数量,
94 def k_means_clust(data, num_clust, num_iter, w=3):
95 ## 步骤一: 初始化均值点
96 centroids = random.sample(list(data), num_clust)
97 counter = 0
98 for n in range(num_iter):
99 counter += 1
100 # print
101 # counter
102 assignments = {} #存储类别0,1,2等类号和所包含的类的号码
103 # 遍历每一个样本点 i ,因为本题与之前有所不同,多了ind的编码
104 for ind, i in enumerate(data):
105 min_dist = float('inf') #最近距离,初始定一个较大的值
106 closest_clust = None # closest_clust:最近的均值点编号
107 ## 步骤二: 寻找最近的均值点
108 for c_ind, j in enumerate(centroids): #每个点和中心点的距离,共有num_clust个值
109 if LB_Keogh(i, j, 3) < min_dist: #循环去找最小的那个
110 cur_dist = DTWDistance(i, j, w)
111 if cur_dist < min_dist: #找到了ind点距离c_ind最近
112 min_dist = cur_dist
113 closest_clust = c_ind
114 ## 步骤三: 更新 ind 所属簇
115 # print(closest_clust)
116 if closest_clust in assignments:
117 assignments[closest_clust].append(ind)
118 else:
119 assignments[closest_clust] = []
120 assignments[closest_clust].append(ind)
121 # recalculate centroids of clusters ## 步骤四: 更新簇的均值点
122 for key in assignments:
123 clust_sum = 0
124 for k in assignments[key]:
125 clust_sum = clust_sum + data[k]
126 centroids[key] = [m / len(assignments[key]) for m in clust_sum]
127 return centroids,assignments
128
129 #
130 num_clust = 2 #定义需要分类的数量
131 centroids,assignments = k_means_clust(WBCData, num_clust,800, 3)
132 for i in range(num_clust):
133 s = []
134 WBC01 = []
135 days01 = []
136 for j, indj in enumerate(assignments[i]): #画出各分类点的坐标
137 s.append(int(Numb[indj*30]))
138 WBC01 = np.hstack((WBC01,WBC[30 * indj:30 * indj + 30]))
139 days01 = np.hstack((days01 , days[0: 30]))
140 print(s)
141 plt.title('%s' % s)
142 plt.plot(centroids[i],c="r",lw=4)
143 plt.scatter(days01, WBC01 )
144 plt.show()


