分类问题的判别标准
目录
- 几个指标的解释FP,FN,TP,TN
- 精确率(Precision),召回率(Recall),准确率(Accuracy)和F值
- RoC曲线和PR曲线
一: 几个指标的解释:FP,FN,TP,TN
刚接触这些评价指标时,感觉很难记忆FP,FN,TP,TN,主要还是要理解,理解后就容易记住了
- P(Positive)和N(Negative) 代表模型的判断结果
- T(True)和F(False) 评价模型的判断结果是否正确
比如FP:模型的判断是正例,实际上这是错误的(F),连起来就是假正例
以此类推:
- True Positives,TP:预测为正样本,实际也为正样本的特征数,预测为正样本是对的
- False Positives,FP:预测为正样本,实际为负样本的特征数,预测为正样本是错的
- True Negatives,TN:预测为负样本,实际也为负样本的特征数,预测为负样本是对的
- False Negatives,FN:预测为负样本,实际为正样本的特征数,预测为负样本是错的
简单理解,如下图所示:
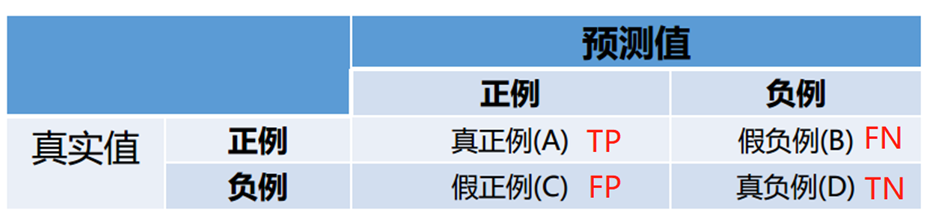
二:精确率(Precision),召回率(Recall),准确率(Accuracy)和F值
准确率(Accuracy):
最直观的就是准确率: 模型判断正确的数据(TP+TN)占总数据的比例

查全率/召回率(Recall):
以真实为正例作为基准:真实值的正例中,被判断出来为正例的概率是多少。
以物体检测为例,我们往往把图片中的物体作为正例,此时召回率高代表着模型可以找出图片中更多的物体。
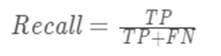
查准率/精确率(Precision):
以判断为正例作为基准:模型判别为正例的里面,实际正确的概率是多少。
精确率高表示模型检测出的物体中大部分确实是物体,只有少量不是物体的对象被当成物体
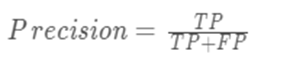
区分好召回率和精确率的关键在于:针对的数据不同,召回率针对的是数据集中的所有正例,精确率针对的是模型判断出的所有正例
F值:
Precision*Recall*2 / (Precision+Recall) (即F值为正确率和召回率的调和平均值)
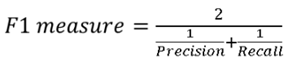
其它(通常比较少见):
此外还有灵敏度(true positive rate ,TPR),它是所有实际正例中,正确识别的正例比例,它和召回率(查全率)的表达式没有区别。严格的数学定义如下:
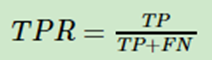
另一个是1-特异度(false positive rate, FPR),它是实际负例中,错误得识别为正例的负例比例。严格的数学定义如下:
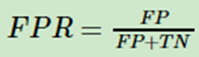
三、 RoC曲线和PR曲线
3.1 ROC(Receiver Operating Characteristic)
最初源于20世纪70年代的信号检测理论,描述的是分类混淆矩阵中FPR-TPR两个量之间的相对变化情况,ROC曲线的纵轴是"真正例率"(True Positive Rate 简称TPR),横轴是"假正例率" (False Positive Rate 简称FPR)。
如果二元分类器输出的是对正样本的一个分类概率值,当取不同阈值时会得到不同的混淆矩阵,对应于ROC曲线上的一个点。那么ROC曲线就反映了FPR与TPR之间权衡的情况,通俗地来说,即在TPR随着FPR递增的情况下,谁增长得更快,快多少的问题。TPR增长得越快,曲线越往上屈,AUC就越大,反映了模型的分类性能就越好。当正负样本不平衡时,这种模型评价方式比起
一般的精确度评价方式的好处尤其显著。
以TPR为y轴,以FPR为x轴,我们就直接得到了RoC曲线。TPR越高,FPR越小,我们的模型和算法就越高效。
3.2 AUC(Area Under Curve)
RoC曲线下的面积,即AUC(Area Under Curve)值来作为算法和模型好坏的标准。AUC的值越大表达模型越好。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围在0.5和1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好,而AUC作为数值可以直观的评价分类器的好坏,值越大越好(最低要求在0.7以上)
- AUC = 1,是完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
- 0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
- AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
- AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜
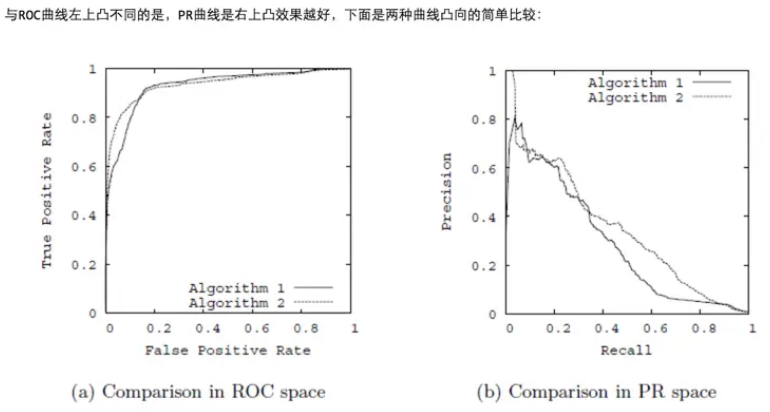
3.3 PR曲线
以精确率为y轴,以召回率为x轴,我们就得到了PR曲线。仍然从精确率和召回率的定义可以理解,精确率越高,召回率越高,我们的模型和算法就越高效。也就是画出来的PR曲线越靠近右上越好。如上图右图所示。
小结:
- 使用RoC曲线和PR曲线,我们就能很方便的评估我们的模型的分类能力的优劣了。
- 实际应用中,应该综合考虑,尤其是数据正负例严重不均衡时或我们意向中允许某种概率可以适当减小(比如判断房颤,10000人中10不正常,你均判断为正常,准确为99.9%,没有任何意义)


