损失函数
目录
- 回归损失函数
- 分类损失函数
- 其他
- 附件证明
机器学习最主要的操作为:模型,损失函数设计,优化问题求解。
损失函数是机器学习中常用于优化模型的目标函数,无论是在分类问题,还是回归问题,都是通过损失函数最小化来求得我们的学习模型的。损失函数分为经验风险损失函数和结构风险损失函数。经验风险损失函数是指预测结果和实际结果的差别,结构风险损失函数是指经验风险损失函数加上正则项。通常表示为:

θ*是我们通过损失函数最小化要求得的参数,一般都是通过梯度下降法来求得。本文主要从回归和分类两大任务讨论损失函数:
一、回归损失函数
1.1 具体形式
绝对值损失函数

平方差损失:
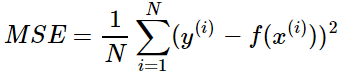
Huber损失函数:两者的结合,δ 是 HuberLoss 的参数,y是真实值,f(x)是模型的预测值, 且由定义可知 Huber Loss 处处可导。GBDT比较常见。

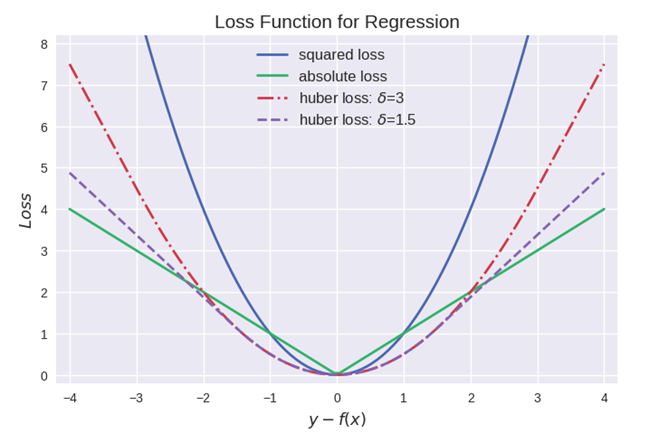
1.2 对比
- 均方误差(MSE mean square error)是回归损失函数中最常用的误差,优点是处处可导;然而其缺点是对于异常点会施以较大的惩罚,因而不够robust。如果有较多异常点,则绝对值损失表现较好
- 平均绝对误差(MAE)的优缺点和MSE相反;
- Huber损失相比于MSE来说对于异常值不敏感,但它同样保持了可微的特性。它基于绝对误差但在误差很小的时候变成了平方误差。我们可以使用超参数δ来调节这一误差的阈值。当δ趋向于0时它就退化成了MAE,而当δ趋向于无穷时则退化为了MSE,其表达式如下,是一个连续可微的分段函数
二、分类损失函数
2.1 具体形式
0-1损失函数:0-1损失函数的表达式如下,常见于感知机模型中,预测正确则损失为0,预测错误则损失为1:

Logistic loss,也称为对数损失(具体推到可见附件一)

Hinge loss :翻译为"合页损失"(具体可见附件二)


常用于SVM中,yf(x)>1的样本损失皆为0,由此带来了稀疏解,使得svm仅通过少量的支持向量就能确定最终超平面。

指数损失函数(具体可见附件三)

指数损失函数常见于Adaboost算法中
modified Huber loss
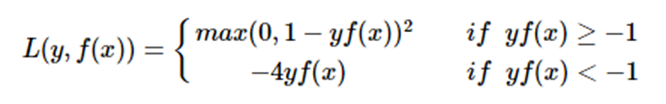
modified huber loss结合了hinge loss和logistic loss的优点,既能在yf(x)>1时产生稀疏解提高训练效率,又能进行概率估计。另外其对(yf(x)<−1) 样本的惩罚以线性增加,这意味着受异常点的干扰较少,比较robust。scikit-learn中的SGDClassifier同样实现了modified huber loss。

交叉熵损失函数(证明见附件四)
1)二分类情况
在二分的情况下,模型最后需要预测的结果只有两种情况,对于每个类别我们的预测得到的概率为p 和 1-p 。此时表达式为:

其中:
- yi —— 表示样本i的label,正类为1,负类为0
- pi —— 表示样本i预测为正的概率
2) 多分类
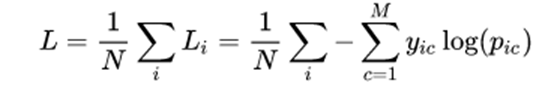
其中:
- M ——类别的数量;
- yic——指示变量(0或1),如果该类别和样本i的类别相同就是1,否则是0;
- pic ——对于观测样本i属于类别 c 的预测概率,注意在log函数内部。
举例说明:

从实例角度出发,确实能够做到模型区分。
2.2 对比
- 0-1损失对每个错分类点都施以相同的惩罚,这样那些"错的离谱" (即 margin→−∞)的点并不会收到大的关注,这在直觉上不是很合适。另外0-1损失不连续、非凸,优化困难,因而常使用其他的代理损失函数进行优化。
- 这些损失函数都可以看作是0-1损失的单调连续近似函数,而因为这些损失函数通常是凸的连续函数,因此常用来代替0-1损失进行优化。它们的相同点是都随着margin→−∞而加大惩罚;不同点在于,logistic loss和hinge loss都是线性增长,而exponential loss是以指数增长。
- 值得注意的是上图中modified huber loss的走向和exponential loss差不多,并不能看出其robust的属性。其实这和算法时间复杂度一样,成倍放大了之后才能体现出巨大差异:

交叉熵损失函数经常用于分类问题中,特别是在神经网络做分类问题时,也经常使用交叉熵作为损失函数,此外,由于交叉熵涉及到计算每个类别的概率,所以交叉熵几乎每次都和sigmoid(或softmax)函数一起出现。
我们用神经网络最后一层输出的情况,来看一眼整个模型预测、获得损失和学习的流程:
- 神经网络最后一层得到每个类别的得分scores;
- 该得分经过sigmoid(或softmax)函数获得概率输出;
- 模型预测的类别概率输出与真实类别的one hot形式进行交叉熵损失函数的计算。
学习任务分为二分类和多分类情况,我们分别讨论这两种情况的学习过程。
三、其他
1、MSE实际上也可以用于分类的损失函数,但是常规应用中并没有使用,那为什么不采样这种损失函数呢?主要原因是逻辑回归配合MSE损失函数时,采用梯度下降法进行学习时,会出现模型一开始训练时,学习速率非常慢的情况
四、附件证明
附件一:Logistic loss证明
logistic Loss为Logistic Regression中使用的损失函数,下面做一下简单证明:Logistic Regression中使用了Sigmoid函数表示预测概率:

![]()
二分类问题中,y属于 -1或1,可统一写成:
![]()
此为一个概率模型,利用极大似然的思想:
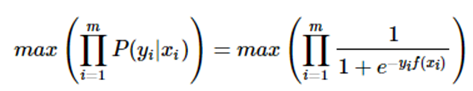
两边取对数,又因为是求损失函数,则将极大转为极小:这样就得到了logistic loss。

另外:
定义如下:
![]()
则极大似然法可写为:

取对数并转为极小得:
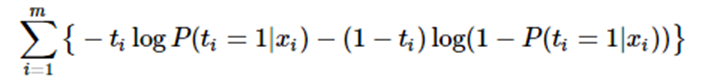
上式被称为交叉熵损失 (cross entropy loss),可以看到在二分类问题中logistic loss和交叉熵损失是等价的,二者区别只是标签y的定义不同。
附件二:Hinge loss证明
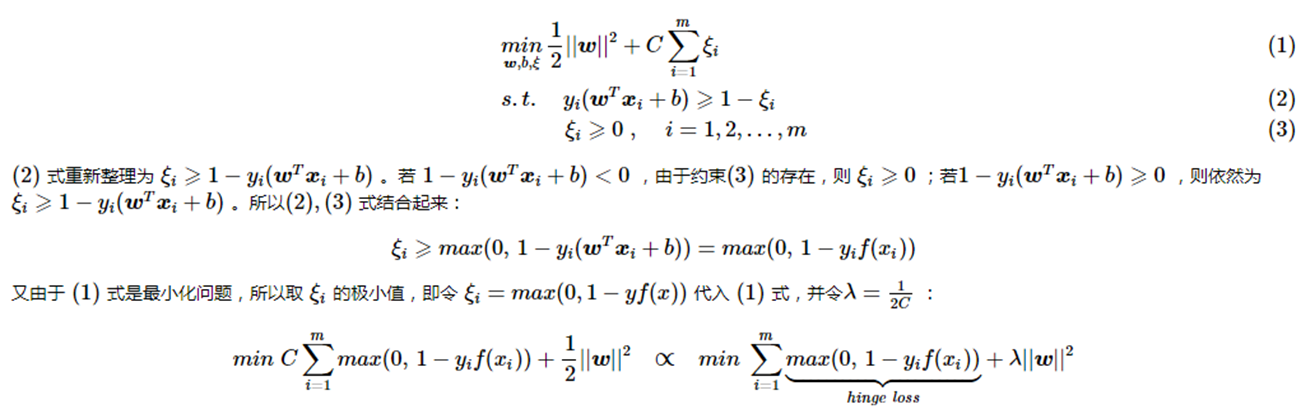
另外可以看到 svm 这个形式的损失函数是自带参数 w 的L2 正则的,而相比之下Logistic Regression的损失函数则没有显式的正则化项,需要另外添加。
附件三:AdaBoost采用指数损失的原因
若将指数损失表示为期望值的形式:
![]()
由于是最小化指数损失,则将上式求导并令其为0:
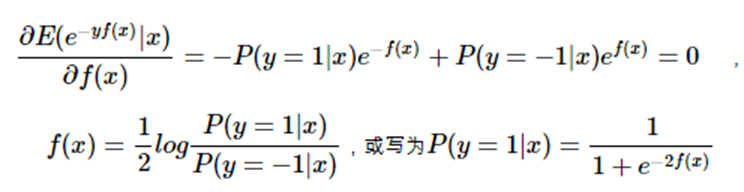
仔细看,这不就是logistic regression吗?二者只差系数1212,因此每一轮最小化指数损失其实就是在训练一个logistic regression模型,以逼近对数几率 (log odds)。

这意味sign(f(x))达到了贝叶斯最优错误率,即对于每个样本xx都选择后验概率最大的类别。若指数损失最小化,则分类错误率也将最小化。这说明指数损失函数是分类任务原本0-1损失函数的一致性替代函数。由于这个替代函数是单调连续可微函数,因此用它代替0-1损失函数作为优化目标。
附件四:交叉熵损失函数
信息量
信息量的大小与信息发生的概率成反比。概率越大,信息量越小。概率越小,信息量越大。设某一事件发生的概率为P(x),其信息量表示为:
![]()
其中I(x)表示信息量,这里log表示以e为底的自然对数。
信息熵
信息熵也被称为熵,用来表示所有信息量的期望。所以信息量的熵可表示为:(这里的X是一个离散型随机变量)

相对熵(KL散度)
如果对于同一个随机变量XX有两个单独的概率分布P(x)和Q(x),则我们可以使用KL散度来衡量这两个概率分布之间的差异。
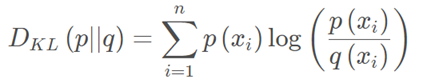
KL散度越小,表示P(x)与Q(x)的分布更加接近,可以通过反复训练Q(x)来使Q(x)的分布逼近P(x)。
交叉熵
首先将KL散度公式拆开:

前者H(p(x))表示信息熵,后者即为交叉熵,KL散度 = - 信息熵 + 交叉熵
交叉熵公式表示为:
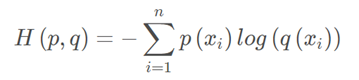
在机器学习训练网络时,输入数据与标签常常已经确定,那么真实概率分布P(x)也就确定下来了,所以信息熵在这里就是一个常量。由于KL散度的值表示真实概率分布P(x)与预测概率分布Q(x)之间的差异,值越小表示预测的结果越好,所以需要最小化KL散度,而交叉熵等于KL散度加上一个常量(信息熵),且公式相比KL散度更加容易计算,所以在机器学习中常常使用交叉熵损失函数来计算loss就行了。
附件四小结:
- 交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度,在机器学习中就表示为真实概率分布与预测概率分布之间的差异。交叉熵的值越小,模型预测效果就越好。
- 交叉熵在分类问题中常常与softmax是标配,softmax将输出的结果进行处理,使其多个分类的预测值和为1,再通过交叉熵来计算损失。
参考文献:
【1】常见回归和分类损失函数比较 https://www.cnblogs.com/massquantity/p/8964029.html

