【ML-8】感知机算法-传统和对偶形式
目录
- 感知机模型
- 感知机模型损失函数
- 感知机模型损失函数的优化方法
- 感知机模型的算法
- 感知机模型的算法对偶形式
我们知道较早的分类模型——感知机(1957年)是二类分类的线性分类模型,也是后来神经网络和支持向量机的基础。
1、感知机模型
感知机模型是一种二分类的线性分类器,只能处理线性可分的问题,感知机的模型就是尝试找到一个超平面将数据集分开,在二维空间这个超平面就是一条直线,在三维空间就是一个平面。

2. 感知机模型损失函数

这样我们就得到了初步的感知机模型的损失函数。
我们研究可以发现,分子和分母都含有θ,当分子的θ扩大N倍时,分母的L2范数也会扩大N倍。也就是说,分子和分母有固定的倍数关系。那么我们可以固定分子或者分母为1,然后求另一个即分子自己或者分母的倒数的最小化作为损失函数,这样可以简化我们的损失函数。在感知机模型中,我们采用的是保留分子,即最终感知机模型的损失函数简化为:
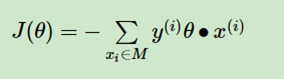
3. 感知机模型损失函数的优化方法

4. 感知机模型的算法

5. 感知机模型的算法对偶形式


转自:https://www.cnblogs.com/pinard/p/6042320.html
感知机算法传统方式实现:
1 import numpy as np
2 from matplotlib import pyplot as plt
3 x=np.array([[1,1],[3,3],[4,3]])
4 y=np.array([[-1],[1],[1]])
5 w=[0,0]
6 b=0
7
8 def Train(x,y,w,b):
9 length = x.shape[0]
10 j=0
11 while True:
12 count=0
13 for i in range(length):
14 print("迭代次数为:%d w=[%d,%d] b=%d"%(j,w[0],w[1],b))
15 if y[i]*(np.dot(w,x[i])+b)<=0: #未被正确分类
16 #更新w,b
17 w=w+y[i]*x[i]
18 b=b+y[i]
19 count+=1
20 j+=1
21 if count==0:
22 f="f(x)=sign(%d*x+%d*x+%d)"%(w[0],w[1],b)
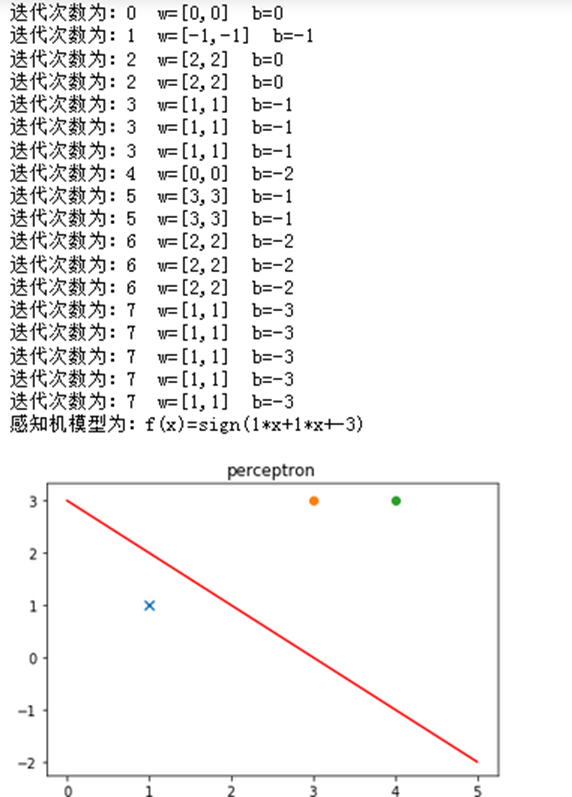
23 print("感知机模型为:%s"%f)
24 return w,b,f
25 w,b,f=Train(x,y,w,b)
26
27 #画分离超平面图
28 def fun(x):
29 y=(-b-w[0]*x)/w[1]
30 return y
31 x_data=np.linspace(0,5)
32 y_data=fun(x_data)
33 plt.plot(x_data,y_data,color='r')
34 plt.title("perceptron")
35
36 #画散点图
37 for i in range(x.shape[0]):
38 if y[i] < 0:
39 plt.scatter(x[i][0], x[i][1], marker='x',s=50)
40 else:
41 plt.scatter(x[i][0], x[i][1])
42 plt.show()
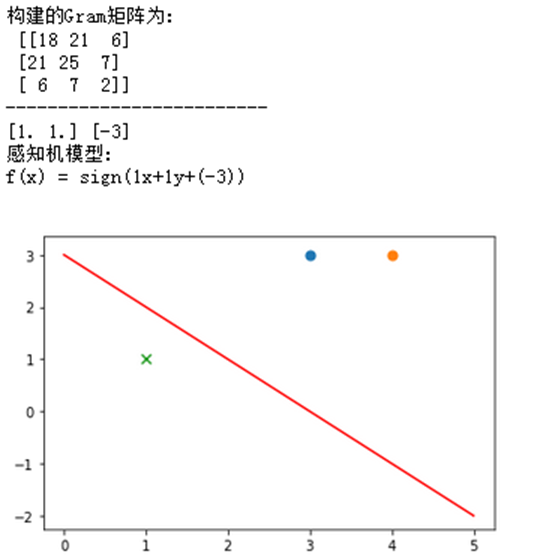
感知机算法的对偶形式
感知机的对偶形式与原始形式并没有多大的区别,运算的过程都是一样的,但通过对偶形式会事先计算好一些步骤的结果并存储到Gray矩阵中,因此可以加快一些运算速度,数据越多节省的计算次数就越多,因此比原始形式更加的优化
import numpy as np
import matplotlib.pyplot as plt
x = np.array([[3, 3], [4, 3], [1, 1]])
y = np.array([[1], [1], [-1]])
# 创建gram矩阵
z = np.transpose(x)
m = np.dot(x,z)
print("构建的Gram矩阵为:\n",m)
print("-------------------------")
a = np.zeros((x.shape[0], 1))
b = 0
def train(x,y,m,a,b):
length = x.shape[0]
while True:
count = 0
for i in range(length):
n = np.dot(m[i], a * y ) + b
if n* y[i] <= 0:
a[i] = a[i] + 1
b = b + y[i]
count += 1
if count == 0:
w = np.sum(x * a* y, axis=0)
print(w,b)
print("感知机模型:\nf(x) = sign(%dx+%dy+(%d))\n"%(w[0],w[1],b))
return w,b
w,b = train(x,y,m,a,b)
def fun(x):
y = (-b -w[0] * x) / w[1]
return y
x_data = np.linspace(0, 5, 100) # 创建等差数组
y_data = fun(x_data)
plt.plot(x_data, y_data, color='r', label='y1 data')
for i in range(x.shape[0]):
if y[i] < 0:
plt.scatter(x[i][0], x[i][1], marker='x', s=50)
else:
plt.scatter(x[i][0], x[i][1], s=50)
plt.show()