【ML-6-1】集成学习-bagging(随机森林)
目录
- 简述集成学习
- bagging算法介绍
- 随机森林
- 随机森林的推广
- 随机森林小结
一、简述集成学习
集成学习(ensemble learning)可以说是非常火爆的机器学习方法。它本身不是一个单独的机器学习算法,而是通过构建并结合多个机器学习器来完成学习任务。也就是我们常说的"博采众长"。集成学习可以用于分类问题集成,回归问题集成,特征选取集成,异常点检测集成等等,可以说所有的机器学习领域都可以看到集成学习的身影。本文就对集成学习的原理做一个总结。集成算法可以分为同质集成和异质集成:
- 同质集成是值集成算法中的个体学习器都是同一类型的学习器,比如都是决策树;
-
异质集成是集成算法中的个体学习器由不同类型的学习器组成的。(目前比较流行的集成算法都是同质算法,而且基本都是基于决策树或者神经网络的)

集成算法是由多个弱学习器组成的算法,而对于这些弱学习器我们希望每个学习器的具有较好的准确性、而且各个学习器之间又存在较大的差异性,这样的集成算法才会有较好的结果,然而实际上准确性和多样性往往是相互冲突的,这就需要我们去找到较好的临界点来保证集成算法的效果。根据个体学习器的生成方式不同,我们可以将集成算法分成两类:
- 个体学习器之间不存在强依赖关系,可以并行化生成每个个体学习器,这一类的代表是Bagging(常见的算法有RandomForest)。
-
个体学习器之间存在强依赖关系,必须串行化生成的序列化方法,这一类的代表是Boosting(常见的算法有Adaboost、GBDT);

本文只介绍第一类:Bagging(实例:RandomForest)
二、bagging算法介绍
2.1 原理
Bagging的原理如下图所示。

随机采样(bootsrap)就是从我们的训练集里面采集固定个数的样本,但是每采集一个样本后,都将样本放回。也就是说,之前采集到的样本在放回后有可能继续被采集到。对于我们的Bagging算法,一般会随机采集和训练集样本数m一样个数的样本。这样得到的采样集和训练集样本的个数相同,但是样本内容不同。如果我们对有m个样本训练集做T次的随机采样,则由于随机性,T个采样集各不相同。特点如下:
- 对于这部分大约36.8%的没有被采样到的数据,我们常常称之为袋外数据(Out Of Bag, 简称OOB)。这些数据没有参与训练集模型的拟合,因此可以用来检测模型的泛化能力。
- bagging对于弱学习器没有限制,这和Adaboost一样。但是最常用的一般也是决策树和神经网络。
- bagging的集合策略也比较简单,对于分类问题,通常使用简单投票法,得到最多票数的类别或者类别之一为最终的模型输出。对于回归问题,通常使用简单平均法,对T个弱学习器得到的回归结果进行算术平均得到最终的模型输出。
- 由于Bagging算法每次都进行采样来训练模型,因此泛化能力很强,对于降低模型的方差很有作用。当然对于训练集的拟合程度就会差一些,也就是模型的偏倚会大一些。
2.2 流程:
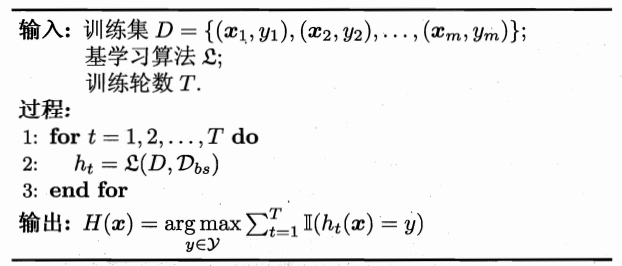
如果是分类算法预测,则T个弱学习器投出最多票数的类别或者类别之一为最终类别。
如果是回归算法,T个弱学习器得到的回归结果进行算术平均得到的值为最终的模型输出。
三、随机森林
3.1 原理
随机森林(Random Forest,以下简称RF)是Bagging算法的进化版,也就是说,它的思想仍然是bagging。可以理解为 RF =bagging + CART。
在使用决策树的基础上,RF对决策树的建立做了改进,对于普通的决策树,我们会在节点上所有的n个样本特征中选择一个最优的特征来做决策树的左右子树划分,但是RF通过随机选择节点上的一部分样本特征,这个数字小于n,假设为nsub,然后在这些随机选择的nsub个样本特征中,选择一个最优的特征来做决策树的左右子树划分。这样进一步增强了模型的泛化能力。
如果nsub=n,则此时RF的CART决策树和普通的CART决策树没有区别。nsub越小,则模型约健壮,当然此时对于训练集的拟合程度会变差。也就是说nsub越小,模型的方差会减小,但是偏倚会增大。在实际案例中,一般会通过交叉验证调参获取一个合适的nsub的值。
3.2 流程:
- 从原始样本集(n个样本)中用Bootstrap采样(有放回重采样)选出n个样本;
- 从所有属性中随机选择K个属性,选择出最佳分割属性作为节点创建决策树;
- 重复以上两步m次,即建立m棵决策树;
- 这m个决策树形成随机森林,通过投票表决结果决定数据属于那一类
四、随机森林的推广
由于RF在实际应用中的良好特性,基于RF,有很多变种算法,应用也很广泛,不光可以用于分类回归,还可以用于特征转换,异常点检测等。下面对于这些RF家族的算法中有代表性的做一个总结。
4.1 extra trees
extra trees是RF的一个变种, 原理几乎和RF一样,仅有区别有:
- RF会随机采样来作为子决策树的训练集,而Extra Tree每个子决策树采用原始数据集训练;
- 在选定了划分特征后,RF的决策树会基于基尼系数,均方差之类的原则,选择一个最优的特征值划分点,这和传统的决策树相同。但是extra trees比较的激进,他会随机的选择一个特征值来划分决策树。
从第二点可以看出,由于随机选择了特征值的划分点位,而不是最优点位,这样会导致决策树的规模一般大于
RF所生成的决策树。也就是说Extra Tree模型的方差相对于RF进一步减少。在某些情况下,Extra Tree的泛化能力比RF的强。
4.2 Totally Random Trees Embedding
Totally Random Trees Embedding(以下简称 TRTE)是一种非监督学习的数据转化方法。它将低维的数据集映射到高维,从而让映射到高维的数据更好的运用于分类回归模型。我们知道,在支持向量机中运用了核方法来将低维的数据集映射到高维,此处TRTE提供了另外一种方法。
TRTE在数据转化的过程也使用了类似于RF的方法,建立T个决策树来拟合数据。当决策树建立完毕以后,数据集里的每个数据在T个决策树中叶子节点的位置也定下来了。
案例:我们有3颗决策树,每个决策树有5个叶子节点,某个数据特征x划分到第一个决策树的第2个叶子节点,第二个决策树的第3个叶子节点,第三个决策树的第5个叶子节点。则x映射后的特征编码为(0,1,0,0,0, 0,0,1,0,0, 0,0,0,0,1), 有15维的高维特征。这里特征维度之间加上空格是为了强调三颗决策树各自的子编码。
映射到高维特征后,可以继续使用监督学习的各种分类回归算法了。
4.3 Isolation Forest(IForest)
IForest是一种异常点检测算法,使用类似RF的方式来检测异常点;IForest算法和RF算法的区别在于:
- 在随机采样的过程中,一般只需要少量数据即可;
- 在进行决策树构建过程中,IForest算法会随机选择一个划分特征,并对划分特征随机选择一个划分阈值;
- IForest算法构建的决策树一般深度max_depth是比较小的。
区别原因:目的是异常点检测,所以只要能够区分异常的即可,不需要大量数据;另外在异常点检测的过程中,一般不需要太大规模的决策树。
对于异常点的判断,则是将测试样本x拟合到T棵决策树上。计算在每棵树上该样本的叶子节点的深度ht(x)。从而计算出平均深度h(x);然后就可以使用下列公式计算样本点x的异常概率值,p(s,m)的取值范围为[0,1],越接近于1,则是异常点的概率越大。

五、 随机森林小结
RF的主要优点:
- 训练可以并行化,对于大规模样本的训练具有速度的优势;
- 由于进行随机选择决策树划分特征列表,这样在样本维度比较高的时候,仍然具有比较高的训练性能;
- 在训练后,可以给出各个特征的重要性列表;
- 由于存在随机抽样,训练出来的模型方差小,泛化能力强;
- 相对于Boosting系列的Adaboost和GBDT,RF实现简单;
- 对于部分特征的缺失不敏感。
RF的主要缺点:
- 在某些噪音比较大的特征上,RF模型容易陷入过拟合;
- 取值比较多的划分特征对RF的决策会产生更大的影响,从而有可能影响模型的效果
附件一:RF scikit-learn相关参数

附件二:
1 # Author:yifan
2
3 import numpy as np
4 import pandas as pd
5 import matplotlib.pyplot as plt
6 import matplotlib as mpl
7 from sklearn import tree
8 from sklearn.ensemble import RandomForestClassifier
9 from sklearn.model_selection import train_test_split
10 from sklearn.pipeline import Pipeline
11 from sklearn.model_selection import GridSearchCV
12 from sklearn.preprocessing import MinMaxScaler
13 from sklearn.decomposition import PCA
14 from sklearn.preprocessing import Imputer
15 from sklearn.preprocessing import label_binarize
16 from sklearn import metrics
17
18 ## 设置属性防止中文乱码
19 mpl.rcParams['font.sans-serif'] = [u'SimHei']
20 mpl.rcParams['axes.unicode_minus'] = False
21
22 names = [u'Age', u'Number of sexual partners', u'First sexual intercourse',
23 u'Num of pregnancies', u'Smokes', u'Smokes (years)',
24 u'Smokes (packs/year)', u'Hormonal Contraceptives',
25 u'Hormonal Contraceptives (years)', u'IUD', u'IUD (years)', u'STDs',
26 u'STDs (number)', u'STDs:condylomatosis',
27 u'STDs:cervical condylomatosis', u'STDs:vaginal condylomatosis',
28 u'STDs:vulvo-perineal condylomatosis', u'STDs:syphilis',
29 u'STDs:pelvic inflammatory disease', u'STDs:genital herpes',
30 u'STDs:molluscum contagiosum', u'STDs:AIDS', u'STDs:HIV',
31 u'STDs:Hepatitis B', u'STDs:HPV', u'STDs: Number of diagnosis',
32 u'STDs: Time since first diagnosis', u'STDs: Time since last diagnosis',
33 u'Dx:Cancer', u'Dx:CIN', u'Dx:HPV', u'Dx', u'Hinselmann', u'Schiller',
34 u'Citology', u'Biopsy']#df.columns
35 path = "datas/risk_factors_cervical_cancer.csv" # 数据文件路径
36 data = pd.read_csv(path)
37
38 ## 模型存在多个需要预测的y值,如果是这种情况下,简单来讲可以直接模型构建,在模型内部会单独的处理每个需要预测的y值,相当于对每个y创建一个模型
39 X = data[names[0:-4]]
40 Y = data[names[-4:]]
41 # print(X.head(1))#随机森林可以处理多个目标变量的情况
42
43 #空值的处理
44 X = X.replace("?", np.NAN)
45 # 使用Imputer给定缺省值,默认的是以mean
46 # 对于缺省值,进行数据填充;默认是以列/特征的均值填充
47 imputer = Imputer(missing_values="NaN")
48 X = imputer.fit_transform(X, Y)
49
50 #数据分割
51 x_train,x_test,y_train,y_test = train_test_split(X, Y, test_size=0.2, random_state=0)
52 # print ("训练样本数量:%d,特征属性数目:%d,目标属性数目:%d" % (x_train.shape[0],x_train.shape[1],y_train.shape[1]))
53 # print ("测试样本数量:%d" % x_test.shape[0])
54
55 #标准化
56 ss = MinMaxScaler()#分类模型,经常使用的是minmaxscaler归一化,回归模型经常用standardscaler
57 x_train = ss.fit_transform(x_train, y_train)
58 x_test = ss.transform(x_test)
59
60 #降维
61 pca = PCA(n_components=2)
62 x_train = pca.fit_transform(x_train)
63 x_test = pca.transform(x_test)
64 x_train.shape
65 print(pca.explained_variance_ratio_)
66
67 #随机森林模型
68 ### n_estimators:迭代次数,每次迭代为Y产生一个模型
69 forest = RandomForestClassifier(n_estimators=100, criterion='gini', max_depth=1, random_state=0)
70 forest.fit(x_train, y_train) #max_depth一般不宜设置过大,把每个模型作为一个弱分类器
71
72 #模型效果评估
73 score = forest.score(x_test, y_test)
74 print ("准确率:%.2f%%" % (score * 100))
75 #模型预测
76 forest_y_score = forest.predict_proba(x_test) # prodict_proba输出概率
77 #计算ROC值
78 # label_binarize(['a','a','b','b'],classes=('a','b','c')).T[:-1].T.ravel()
79 #上面的结果:array([1, 0, 1, 0, 0, 1, 0, 1])
80 forest_fpr1, forest_tpr1, _ = metrics.roc_curve(label_binarize(y_test[names[-4]],classes=(0,1,2)).T[0:-1].T.ravel(), forest_y_score[0].ravel())
81 forest_fpr2, forest_tpr2, _ = metrics.roc_curve(label_binarize(y_test[names[-3]],classes=(0,1,2)).T[0:-1].T.ravel(), forest_y_score[1].ravel())
82 forest_fpr3, forest_tpr3, _ = metrics.roc_curve(label_binarize(y_test[names[-2]],classes=(0,1,2)).T[0:-1].T.ravel(), forest_y_score[2].ravel())
83 forest_fpr4, forest_tpr4, _ = metrics.roc_curve(label_binarize(y_test[names[-1]],classes=(0,1,2)).T[0:-1].T.ravel(), forest_y_score[3].ravel())
84 #AUC值
85 auc1 = metrics.auc(forest_fpr1, forest_tpr1)
86 auc2 = metrics.auc(forest_fpr2, forest_tpr2)
87 auc3 = metrics.auc(forest_fpr3, forest_tpr3)
88 auc4 = metrics.auc(forest_fpr4, forest_tpr4)
89
90 print ("Hinselmann目标属性AUC值:", auc1)
91 print ("Schiller目标属性AUC值:", auc2)
92 print ("Citology目标属性AUC值:", auc3)
93 print ("Biopsy目标属性AUC值:", auc4)
94
95 # 正确的数据
96 y_true = label_binarize(y_test[names[-4]],classes=(0,1,2)).T[0:-1].T.ravel()
97 # 预测的数据 => 获取第一个目标属性的预测值,并将其转换为一维的数组
98 y_predict = forest_y_score[0].ravel()
99 # 计算的值
100 metrics.roc_curve(y_true, y_predict)
101
102
103 ## 8. 画图(ROC图)
104 plt.figure(figsize=(8, 6), facecolor='w')
105 plt.plot(forest_fpr1,forest_tpr1,c='r',lw=2,label=u'Hinselmann目标属性,AUC=%.3f' % auc1)
106 plt.plot(forest_fpr2,forest_tpr2,c='b',lw=2,label=u'Schiller目标属性,AUC=%.3f' % auc2)
107 plt.plot(forest_fpr3,forest_tpr3,c='g',lw=2,label=u'Citology目标属性,AUC=%.3f' % auc3)
108 plt.plot(forest_fpr4,forest_tpr4,c='y',lw=2,label=u'Biopsy目标属性,AUC=%.3f' % auc4)
109 plt.plot((0,1),(0,1),c='#a0a0a0',lw=2,ls='--')
110 plt.xlim(-0.001, 1.001)
111 plt.ylim(-0.001, 1.001)
112 plt.xticks(np.arange(0, 1.1, 0.1)) #设置横坐标范围和间隔
113 plt.yticks(np.arange(0, 1.1, 0.1))
114 plt.xlabel('False Positive Rate(FPR)', fontsize=16)
115 plt.ylabel('True Positive Rate(TPR)', fontsize=16)
116 plt.grid(b=True, ls=':')
117 plt.legend(loc='lower right', fancybox=True, framealpha=0.8, fontsize=12)
118 plt.title(u'随机森林多目标属性分类ROC曲线', fontsize=18)
119 plt.show()
120
121 # 比较不同树数目、树最大深度的情况下随机森林的正确率
122 # 一般情况下,初始的随机森林树个数是100,深度1,如果需要我们再进行优化操作
123 x_train2, x_test2, y_train2, y_test2 = train_test_split(X, Y, test_size=0.5, random_state=0)
124 print("训练样本数量%d,测试样本数量:%d" % (x_train2.shape[0], x_test2.shape[0]))
125 ## 比较
126 estimators = [1, 50, 100, 500]
127 depth = [1, 2, 3, 7, 15]
128 err_list = []
129 for es in estimators:
130 es_list = []
131 for d in depth:
132 tf = RandomForestClassifier(n_estimators=es, criterion='gini', max_depth=d, max_features=None, random_state=0)
133 tf.fit(x_train2, y_train2)
134 st = tf.score(x_test2, y_test2)
135 err = 1 - st
136 es_list.append(err)
137 print("%d决策树数目,%d最大深度,正确率:%.2f%%" % (es, d, st * 100))
138 err_list.append(es_list)
139
140 ## 画图
141 plt.figure(facecolor='w')
142 i = 0
143 colors = ['r', 'b', 'g', 'y']
144 lw = [1, 2, 4, 3]
145 max_err = 0
146 min_err = 100
147 for es, l in zip(estimators, err_list):
148 plt.plot(depth, l, c=colors[i], lw=lw[i], label=u'树数目:%d' % es)
149 max_err = max((max(l), max_err))
150 min_err = min((min(l), min_err))
151 i += 1
152 plt.xlabel(u'树深度', fontsize=16)
153 plt.ylabel(u'错误率', fontsize=16)
154 plt.legend(loc='upper left', fancybox=True, framealpha=0.8, fontsize=12)
155 plt.grid(True)
156 plt.xlim(min(depth), max(depth))
157 plt.ylim(min_err * 0.99, max_err * 1.01)
158 plt.title(u'随机森林中树数目、深度和错误率的关系图', fontsize=18)
159 plt.show()
结果:


训练样本数量429,测试样本数量:429
1决策树数目,1最大深度,正确率:86.48%
1决策树数目,2最大深度,正确率:86.95%
1决策树数目,3最大深度,正确率:84.62%
1决策树数目,7最大深度,正确率:82.75%
1决策树数目,15最大深度,正确率:78.09%
50决策树数目,1最大深度,正确率:86.71%
50决策树数目,2最大深度,正确率:86.48%
50决策树数目,3最大深度,正确率:86.48%
50决策树数目,7最大深度,正确率:86.25%
50决策树数目,15最大深度,正确率:84.38%
100决策树数目,1最大深度,正确率:86.95%
100决策树数目,2最大深度,正确率:86.25%
100决策树数目,3最大深度,正确率:86.48%
100决策树数目,7最大深度,正确率:86.25%
100决策树数目,15最大深度,正确率:85.08%
500决策树数目,1最大深度,正确率:86.48%
500决策树数目,2最大深度,正确率:86.48%
500决策树数目,3最大深度,正确率:86.48%
500决策树数目,7最大深度,正确率:86.25%
500决策树数目,15最大深度,正确率:84.85%



