【ML-5】决策树算法
一、目录
- 目录
- 决策树初步认知
- 决策树--ID3算法
- 决策树--C4.5算法
- 决策树--CART
- CART算法的剪枝
- 决策树的优缺点
- 其他补充
- 总结
二、决策树初步认知
决策树算法在机器学习中算是很经典的一个算法系列了。它先按照影响结果的主要因素进行排序,选取最主要的因素先进行分岔,依次循环下去。各种方法不同之处在于选择的因素判别方法不同。
它既可以作为分类算法,回归算法,同时也特别适合集成学习比如随机森林。作为一个码农经常会不停的敲if-else 。If-else其实就已经在用到决策树的思想了:关于递归的终止条件有三种情形:
1)当前节点包含的样本属于同一类,则无需划分,该节点作为叶子节点,该节点输出的类别为样本的类别
2)该节点包含的样本集合为空,不能划分
3)当前属性集为空,则无法划分,该节点作为叶子节点,该节点的输出类别为样本中数量多数的类别
本文就对ID3, C4.5和CART算法做一个详细的介绍。选择CART做重点介绍的原因是scikit-learn使用了优化版的CART算法作为其决策树算法的实现。
三、决策树--ID3算法
1970年代,一个叫昆兰的大牛找到了用信息论中的熵来度量决策树的决策选择过程,方法一出,它的简洁和高效就引起了轰动,昆兰把这个算法叫做ID3。
1.1 信息熵
首先,我们需要熟悉信息论中熵的概念。熵度量了事物的不确定性,越不确定的事物,它的熵就越大。具体的,随机变量X的熵的表达式如下:

又可以得到条件熵的表达式H(X|Y),条件熵类似于条件概率,它度量了我们的X在知道Y以后剩下的不确定性。表达式如下:

在决策树ID3算法中叫做信息增益。ID3算法就是用信息增益来判断当前节点应该用什么特征来构建决策树。信息增益大(信息熵减小最快的因素),则越适合用来分类。其他熵的了解,可见我的另一篇文章。
1.2 ID3算法
在ID3算法中用的是信息增益作为选择特征的指标,信息增益的定义是在特征A给定的条件下,集合D的信息熵H(D) 和在 特征A条件下的条件熵H(D|A) 的差值,描述了选取特征A对数据集进行划分对信息熵的减小程度,信息增益的表达式:
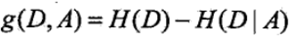
具体的信息增益计算过程如下:
1)计算数据集D的信息熵H(D):
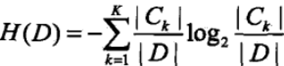
2)计算特征A对数据集D的条件熵H(D|A):
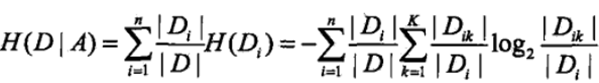
3)计算信息增益g(D, A)

因此ID3算法的流程就很简单了,每次都采用信息增益来选取最优划分特征来划分数据集,直到遇到了递归终止条件,具体算法流程如下:
定义输入值:训练数据集D,特征集A(可以从训练集中提取出来),阀值ε(用来实现提前终止);

2)若A为空,则将当前结点作为叶子节点,并将数据集中数量最多的类作为该结点输出类;
3)否则,计算所有特征的信息增益,若此时最大的信息增益小于阀值ε,则将当前结点作为叶子节点,并将数据集中数量最多的类作为该结点输出类;
4)若当前的最大信息增益大于阀值ε,则将最大信息增益对应的特征A作为最优划分特征对数据集进行划分,根据特征A的取值将数据集划分为若干个子集;
5)对第i个结点,以Di为训练集,以Ai为特征集(将之前用过的特征从特征集中去除),递归的调用前面的1- 4 步。

1.3 ID3算法的不足
- ID3算法采用信息增益来选择最优划分特征,然而人们发现,信息增益倾向与取值较多的特征,对于这种具有明显倾向性的属性,往往容易导致结果误差(后面的C4.5利用信息增益比规避这一点);
- ID3算法没有考虑连续值,对与连续值的特征无法进行划分;
- 不是递增算法(每个特征只用一次)
- 抗噪性差,若有噪音,肯定会再建立一类
- ID3算法无法处理有缺失值的数据;
- ID3算法没有考虑过拟合的问题,而在决策树中,过拟合是很容易发生的;
- ID3算法采用贪心算法,每次划分都是考虑局部最优化,而局部最优化并不是全局最优化,当然这一缺点也是决策树的缺点,获得最优决策树本身就是一个NP难题,所以只能采用局部最优;
四、决策树--C4.5算法
C4.5算法的提出旨在解决ID3算法的缺点 ,因此讲解C4.5算法我们从ID3算法的缺点出发:
1)采用信息增益比来替代信息增益作为寻找最优划分特征,信息增益比的定义是信息增益和特征熵的比值,对于特征熵,特征的取值越多,特征熵就倾向于越大;
信息增益比的表达式如下:
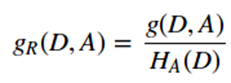
其中和
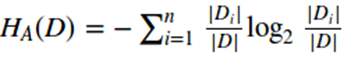
n是特征A取值的个数。
2)对于连续值的问题,将连续值离散化,在这里只作二类划分,即将连续值划分到两个区间,划分点取两个临近值的均值,因此对于m个连续值总共有m-1各划分点,对于每个划分点,依次算它们的信息增益,选取信息增益最大的点作为离散划分点;
3)对于缺失值的问题,我们需要解决两个问题:
第一是在有缺失值的情况下如何选择划分的属性,也就是如何得到一个合适的信息增益比;
第二是选定了划分属性,对于在该属性的缺失特征的样本该如何处理。
对于第一个问题,对于某一个有缺失特征值的特征A。C4.5的思路是将数据分成两部分,对每个样本设置一个权重(初始可以都为1),然后划分数据,一部分是有特征值A的数据D1,另一部分是没有特征A的数据D2. 然后对于没有缺失特征A的数据集D1来和对应的A特征的各个特征值一起计算加权重后的信息增益比,最后乘上一个系数(有特征和全体的比值)
对于第二个子问题,可以将缺失特征的样本同时划分入所有的子节点,不过将该样本的权重按各个子节点样本的数量比例来分配。比如缺失特征A的样本a之前权重为1,特征A有3个特征值A1,A2,A3。 3个特征值对应的无缺失A特征的样本个数为2,3,4。则a同时划分入A1,A2,A3。对应权重调节为2/9,3/9,4/9;
4)对于过拟合的问题,采用了后剪枝算法和交叉验证对决策树进行剪枝处理,这个在CART算法中一起介绍。除了上面的4点,C4.5和ID3的思路区别不大。
C4.5几个缺点:
- 产生的规则易于理解
- 准确率较高
- 实现简单
C4.5几个缺点:
- C4.5的剪枝算法不够优秀;
- C4.5和ID3一样,都是生成的多叉树,然而在计算机中二叉树模型会比多叉树的运算效率高,采用二叉树也许效果会更好;
- 在计算信息熵时会涉及到大量的对数运算,如果是连续值还需要进行排序,寻找最优离散划分点,这些都会增大模型的运算;
- C4.5算法只能处理分类问题,不能处理回归问题,限制了其应用范围。
- 只适合小规模数据集,需要将数据放到内存中
补充:C5算法是商业算法,也是从C4.5的基础上发展而来。
五、决策树--CART
分类与回归树(Classification and Regression Trees, CART)是在C4.5算法的基础上对其缺点进行改进的算法,采用二叉树作为树模型的基础结构,采用基尼指数(分类问题)和和方差(回归问题)属性来选取最优划分特征。CART算法由以下两部组成:
- 决策树生成:基于训练集极大可能的生成决策树(事实上,在生成树的过程中可以加入一些阀值,对决策树做一些预剪枝处理,配合之后的后剪枝效果会更好);
- 决策树剪枝:用验证数据集对已生成的树进行剪枝并选择最优子树,这时用损失函数最小作为剪枝的标准(寻找全局最优子树)。
基尼指数:
基尼指数也可以表述数据集D的不确定性,基尼指数越大,样本集合的不确定性就越大,对于给定的样本集,假设有k个类别,第k个类别的概率为Pk,则基尼指数的表达式为:
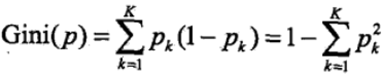
对于给定的样本集合D,其基尼指数可以表述为:

在给定特征A的情况下,若集合被特征A的取值给分成D1和D2 ,则在特征A的条件下的基尼指数可以表述为:
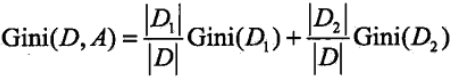
因此在进行最优划分特征选择时,我们选择在该特征下基尼指数最小(和之前熵一样,就是朝着确定性方向走的最大的)的特征,而且在二分类的问题中基尼指数和熵的差异不大,基尼指数和熵之半(熵的一半)的曲线如下

引入基尼指数解决了计算熵时大量的对数运算的问题,然而CART树是二叉树,那么我们在选取了特征之后,又该如何划分数据集呢?
1)对于连续值
在C4.5中我们对于连续值的处理就是将其划分为两类,那么在CART中更是如此,划分方式和C4.5算法一样,唯一的区别是度量方式不同,在CART中采用选择使得在该特征下基尼指数最小的划分点来将连续值划分为两类;
2)对于离散值
对与离散值的处理和ID3或者C4.5都有很大的不同,对于某个特征A,其取值可能不只两个,对于取值大于2的,我们需要随意组合将其分为两类,选择基尼指数最小的那一类作为当前的划分(因为对与特征A,并没有将其按照取值完全分开,所以此时特征A不会从特征集中去除,会留到之后可能再被选择,这也是和ID3、C4.5不同的地方)。
对于CART分类树的算法流程和C4.5差不多,只要注意每次都是进行二类划分,即使该特征的取值有多个。
CART回归树
回归树模型:

均方误差如下图所示,可以通过最小二乘法进行预测和优化。
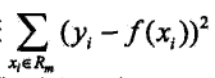
CART回归树其算法流程和CART分类树差不多,但在细节上有些不同,以二叉树为例进行分析,主要是以下两个方面:
1)对连续值的处理方式不一样,采用的特征选择属性不一样,在这里采用的是常用的和方差来进行特征选择,其表达式如下:
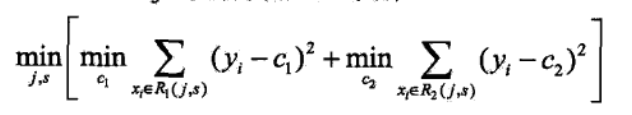
对于任意特征A,对应的任意划分点将数据集划分成D1和D2两个部分,寻找到使得D1和D2各自集合的均方误差最小,并且D1和D2的均方误差之和也最小的划分点,该划分点就是该特征最佳的划分点,因此利用和方差选取最优特征时,就是选取使得和方差最小的特征和划分点。
2)决策树的预测方式不一样,在分类算法中都是采用叶子结点中数量最多的类别作为输出值,而对于回归问题,一般采用叶子结点中的样本集的均值或者中位数作为输出值,有的还会基于叶子结点中的集合建立线性回归模型来作为输出值。
CART算法缺点:
1)每次用最优特征进行划分,这种贪心算法很容易陷入局部最优,事实上分类决策不应该由某一特征决定,而是一组特征决定的,比如多变量决策树(事实上我觉得还不如用集成算法);
2)样本敏感性,样本的一点改动足以影响整个树的结构,也可以通过集成算法解决;
六、CART算法的剪枝
无论是对于分类树还是回归树,都可以用同样的方式进行剪枝,决策树是非常容易过拟合的,因此对决策树进行剪枝是很有必要的(剪枝说白了就是减小模型的复杂度),具体的剪枝算法如下:
首先我们看看剪枝的损失函数度量,在剪枝的过程中,对于任意的一刻子树T,其损失函数为:
具体的从整体树开始剪枝,对与任意内部结点,以t为单结点数的损失函数是:

当α继续增大时不等式反向,也就是说,如果满足:α=(C(T) − C(Tt)) / (|Tt| − 1),Tt和T有相同的损失函数,但是T节点更少,因此可以对子树Tt进行剪枝,也就是将它的子节点全部剪掉,变为一个叶子节点T。
最后我们看看CART树的交叉验证策略。上面我们讲到,可以计算出每个子树是否剪枝的阈值α,如果我们把所有的节点是否剪枝的值α都计算出来,然后分别针对不同的α所对应的剪枝后的最优子树做交叉验证。这样就可以选择一个最好的α,有了这个α,我们就可以用对应的最优子树作为最终结果。
现在我们现在来看看CART树的剪枝算法:
输入是CART树建立算法得到的原始决策树T;
输出是最优决策子树Tα;
算法过程:

七、决策树的优缺点
决策树的优点:
1)决策树简单直观,相比于如神经网络之类的黑盒模型,决策树容易理解,还可以进行可视化;
2)基本上不需要做预处理,不需要做归一化,不需要处理缺失值;
3)使用决策树进行预测的时间复杂度只有O(log2m),m为样本数;
4)即可以处理离散值,也可以处理连续值,无论数对于分类问题还是回归问题;
5)可以很容易的处理多分类的问题;
6)可以用交叉验证来对决策树进行剪枝,避免过拟合(对于很复杂的决策树,最好配合预剪枝一起处理);
7)对于异常点的容错性好,健壮性高;
决策树的缺点:
1)决策树很容易过拟合,很多时候即使进行后剪枝也无法避免过拟合的问题,因此可以通过设置树深或者叶节点中的样本个数来进行预剪枝控制;
2)决策树属于样本敏感型,即使样本发生一点点改动,也会导致整个树结构的变化,可以通过集成算法来解决;
3)寻找最优决策树是各NP难题,一般是通过启发式方法,这样容易陷入局部最优,可以通过集成算法来解决;
4)决策树无法表达如异或这类的复杂问题;
单独的决策树算法用的不多,决策树大多是作为集成算法的基学习器来用的。
八、其他补充
8.1 各种算法比较:
|
算法 |
支持模型 |
树结构 |
特征选择 |
连续值处理 |
缺失值处理 (一般会提起处理) |
剪枝 |
特征属性多次使用 |
|
ID3 |
分类 |
多叉树 |
信息增益 |
不支持 |
不支持 |
不支持 |
不支持 |
|
C4.5 |
分类 |
多叉树 |
信息增益比 |
支持 |
支持 |
支持 |
不支持 |
|
CART |
分类,回归 |
二叉树 |
基尼系数,均方差 |
支持 |
支持 |
支持 |
支持 |
8.2 树模型参数:别让这个数太庞大,防治过拟合
- 1.criterion gini or entropy gini系数或熵值
- 2.splitter best or random 前者是在所有特征中找最好的切分点 后者是在部分特征中(数据量大的时候)
- 3.max_features None(所有),log2,sqrt,N 特征小于50的时候一般使用所有的
- 4.max_depth 数据少或者特征少的时候可以不管这个值,如果模型样本量多,特征也多的情况下,可以尝试限制下
- 5.min_samples_split 如果某节点的样本数少于min_samples_split,则不会继续再尝试选择最优特征来进行划分如果样本量不大,不需要管这个值。如果样本量数量级非常大,则推荐增大这个值。
- 6.min_samples_leaf 这个值限制了叶子节点最少的样本数,如果某叶子节点数目小于样本数,则会和兄弟节点一起被剪枝,如果样本量不大,不需要管这个值,大些如10W可是尝试下5
- 7.min_weight_fraction_leaf 这个值限制了叶子节点所有样本权重和的最小值,如果小于这个值,则会和兄弟节点一起被剪枝默认是0,就是不考虑权重问题。一般来说,如果我们有较多样本有缺失值,或者分类树样本的分布类别偏差很大,就会引入样本权重,这时我们就要注意这个值了。
- 8.max_leaf_nodes 通过限制最大叶子节点数,可以防止过拟合,默认是"None",即不限制最大的叶子节点数。如果加了限制,算法会建立在最大叶子节点数内最优的决策树。如果特征不多,可以不考虑这个值,但是如果特征分成多的话,可以加以限制具体的值可以通过交叉验证得到。
- 9.class_weight 指定样本各类别的的权重,主要是为了防止训练集某些类别的样本过多导致训练的决策树过于偏向这些类别。这里可以自己指定各个样本的权重如果使用"balanced",则算法会自己计算权重,样本量少的类别所对应的样本权重会高。
- 10.min_impurity_split 这个值限制了决策树的增长,如果某节点的不纯度(基尼系数,信息增益,均方差,绝对差)小于这个阈值则该节点不再生成子节点。即为叶子节点 。
- n_estimators:要建立树的个数
总结:
- ID3和C4.5算法均只适合在小规模数据集上使用
- ID3和C4.5,CART算法都是单变量决策树
- 当属性值取值比较多的时候,最好考虑C4.5算法,ID3得出的效果会比较差
- 决策树分类一般情况只适合小数据量的情况(数据可以放内存)
- CART算法是三种算法中最常用的一种决策树构建算法。
- 三种算法的区别仅仅只是对于当前树的评价标准不同而已,ID3使用信息增益、
- C4.5使用信息增益率、CART使用基尼系数。
- CART算法构建的一定是二叉树,ID3和C4.5构建的不一定是二叉树。
- 分类树和回归树:
9.1 区别:
- 分类树中使用信息熵,gini系数,错误率作为树的"纯度"的度量指标,回归树种使用MESE和MAE作为树的"纯度"指标
- 分类树使用叶子节点种包含最多的那个类别作为当前叶子节点的预测值,回归树中使用叶子节点中包含的所有样本的目标属性的均值作为当前叶子节点的预测值
9.2 决策树构建实现:让每次分裂数据集的时候,使得数据更加"纯"
9.3 分裂属性的选择方式:
- 基于最优化划分的规则进行选择,迭代计算所有特征属性上所有的划分方式后的"纯度",选择划分后更加"纯"的一种方式(信息增益,信息增益比)---只能说明在当前数据集合下是最优的,存在过拟合的问题
- 基于随机的划分规则:每次划分的时候都是先选择一定数目的特征,在这回部分特征中选择一个最优的划分,因为每次都是局部最优,可以增加模型的鲁棒性;
9.4 决策树的欠拟合和过拟合:可以调整树的深度来调整(欠就增加,过就剪枝),使用网路交叉验证(GridSearchCV)
算法:https://github.com/yifanhunter/DecisionTree
1 # Author:yifan
2 import numpy as np
3 import pandas as pd
4 import matplotlib.pyplot as plt
5 import matplotlib as mpl
6 import warnings
7
8 from sklearn.tree import DecisionTreeClassifier #分类树
9 from sklearn.model_selection import train_test_split#测试集和训练集
10 from sklearn.feature_selection import SelectKBest #特征选择
11 from sklearn.feature_selection import chi2 #卡方统计量
12
13 from sklearn.preprocessing import MinMaxScaler #数据归一化
14 from sklearn.decomposition import PCA #主成分分析
15
16 ## 设置属性防止中文乱码
17 mpl.rcParams['font.sans-serif'] = [u'SimHei']
18 mpl.rcParams['axes.unicode_minus'] = False
19
20 warnings.filterwarnings('ignore', category=FutureWarning)
21 # iris_feature_E = 'sepal length', 'sepal width', 'petal length', 'petal width'
22 # iris_feature_C = '花萼长度', '花萼宽度', '花瓣长度', '花瓣宽度'
23 # iris_class = 'Iris-setosa', 'Iris-versicolor', 'Iris-virginica'
24 #读取数据
25 path = './datas/iris.data'
26 data = pd.read_csv(path, header=None)
27 x=data[list(range(4))] #获取X变量
28 y=pd.Categorical(data[4]).codes #把Y转换成分类型的0,1,2
29 # print("总样本数目:%d;特征属性数目:%d" % x.shape) #总样本数目:150;特征属性数目:4
30
31 #数据进行分割(训练数据和测试数据)
32 x_train1, x_test1, y_train1, y_test1 = train_test_split(x, y, train_size=0.8, random_state=14)
33 x_train, x_test, y_train, y_test = x_train1, x_test1, y_train1, y_test1
34 print ("训练数据集样本数目:%d, 测试数据集样本数目:%d" % (x_train.shape[0], x_test.shape[0]))
35 ## 因为需要体现以下是分类模型,因为DecisionTreeClassifier是分类算法,要求y必须是int类型
36 y_train = y_train.astype(np.int)
37 y_test = y_test.astype(np.int)
38
39 ss = MinMaxScaler()
40 x_train = ss.fit_transform(x_train)
41 x_test = ss.transform(x_test)
42 print ("原始数据各个特征属性的调整最小值:",ss.min_)
43 print ("原始数据各个特征属性的缩放数据值:",ss.scale_)
44 #特征选择:从已有的特征中选择出影响目标值最大的特征属性
45 #常用方法:{ 分类:F统计量、卡方系数,互信息mutual_info_classif
46 #{ 连续:皮尔逊相关系数 F统计量 互信息mutual_info_classif
47 #SelectKBest(卡方系数)
48 #在当前的案例中,使用SelectKBest这个方法从4个原始的特征属性,选择出来3个
49 ch2 = SelectKBest(chi2,k=3)
50 #K默认为10 如果指定了,那么就会返回你所想要的特征的个数
51 x_train = ch2.fit_transform(x_train, y_train)#训练并转换
52 x_test = ch2.transform(x_test)#转换
53
54 select_name_index = ch2.get_support(indices=True)
55 print ("对类别判断影响最大的三个特征属性分布是:",ch2.get_support(indices=False)) #[ True False True True]
56 print(select_name_index) #[0 2 3]
57
58 #降维:对于数据而言,如果特征属性比较多,在构建过程中,会比较复杂,这个时候考虑将多维(高维)映射到低维的数据
59 #常用的方法:
60 #PCA:主成分分析(无监督)
61 #LDA:线性判别分析(有监督)类内方差最小,人脸识别,通常先做一次pca
62 pca = PCA(n_components=2)#构建一个pca对象,设置最终维度是2维
63 #这里是为了后面画图方便,所以将数据维度设置了2维,一般用默认不设置参数就可以
64 x_train = pca.fit_transform(x_train) #训练并转换
65 x_test = pca.transform(x_test) #转换
66
67 #模型的构建
68 model = DecisionTreeClassifier(criterion='entropy',random_state=0) #另外也可选gini
69 #模型训练
70 model.fit(x_train, y_train)
71 #模型预测
72 y_test_hat = model.predict(x_test)
73 #模型结果的评估
74 y_test2 = y_test.reshape(-1)
75 result = (y_test2 == y_test_hat)
76 print ("准确率:%.2f%%" % (np.mean(result) * 100)) #准确率:96.67%
77 #实际可通过参数获取
78 print ("Score:", model.score(x_test, y_test))#准确率 #Score: 0.9666666666666667
79 print ("Classes:", model.classes_) #Classes: [0 1 2]
80 print("获取各个特征的权重:", end='') #获取各个特征的权重:[0.93420127 0.06579873]
81 print(model.feature_importances_)
82
83 #画图
84 N = 100 #横纵各采样多少个值
85 # print(x_train.T[0],x_train.T[1])
86 x1_min = np.min((x_train.T[0].min(), x_test.T[0].min()))
87 x1_max = np.max((x_train.T[0].max(), x_test.T[0].max()))
88 x2_min = np.min((x_train.T[1].min(), x_test.T[1].min()))
89 x2_max = np.max((x_train.T[1].max(), x_test.T[1].max()))
90 t1 = np.linspace(x1_min, x1_max, N)
91 t2 = np.linspace(x2_min, x2_max, N)
92 x1, x2 = np.meshgrid(t1, t2) # 生成网格采样点
93 x_show = np.dstack((x1.flat, x2.flat))[0] #测试点
94 y_show_hat = model.predict(x_show) #预测值
95
96 y_show_hat = y_show_hat.reshape(x1.shape) #使之与输入的形状相同
97 # print(y_show_hat.shape)
98
99 #画图
100 plt_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
101 plt_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
102
103 plt.figure(facecolor='w')
104 ## 画一个区域图
105 plt.pcolormesh(x1, x2, y_show_hat, cmap=plt_light)
106 # 画测试数据的点信息
107 plt.scatter(x_test.T[0], x_test.T[1], c=y_test.ravel(), edgecolors='k', s=150, zorder=10, cmap=plt_dark, marker='*') # 测试数据
108 # 画训练数据的点信息
109 plt.scatter(x_train.T[0], x_train.T[1], c=y_train.ravel(), edgecolors='k', s=40, cmap=plt_dark) # 全部数据
110 plt.xlabel(u'特征属性1', fontsize=15)
111 plt.ylabel(u'特征属性2', fontsize=15)
112 plt.xlim(x1_min, x1_max)
113 plt.ylim(x2_min, x2_max)
114 plt.grid(True)
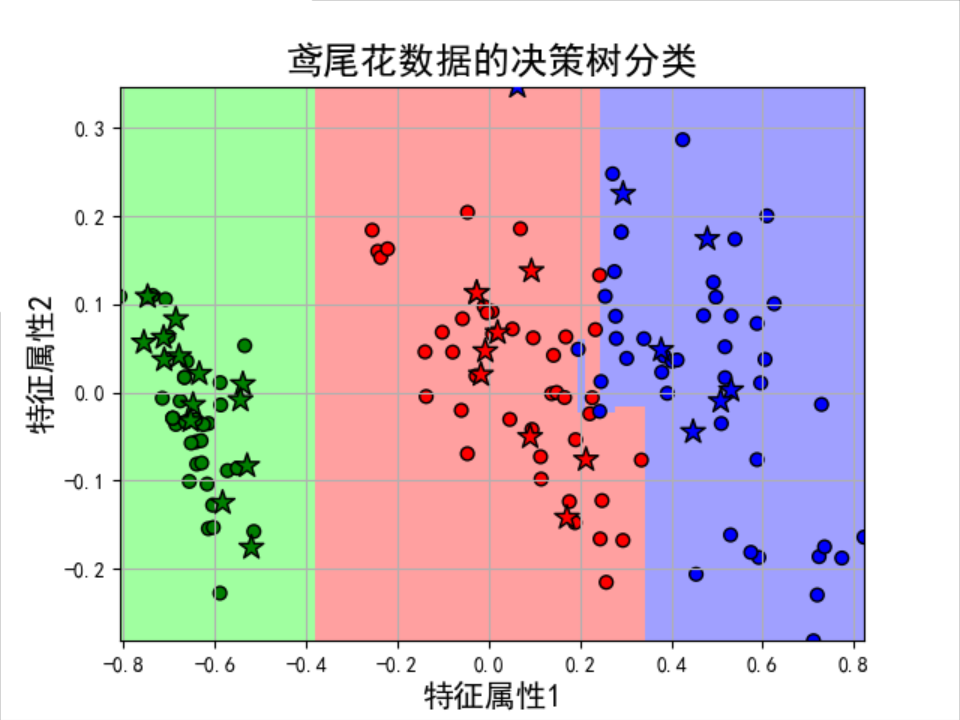
115 plt.title(u'鸢尾花数据的决策树分类', fontsize=18)
116 plt.show()
结果:
训练数据集样本数目:120, 测试数据集样本数目:30
原始数据各个特征属性的调整最小值: [-1.19444444 -0.83333333 -0.18965517 -0.04166667]
原始数据各个特征属性的缩放数据值: [0.27777778 0.41666667 0.17241379 0.41666667]
对类别判断影响最大的三个特征属性分布是: [ True False True True]
[0 2 3]
准确率:96.67%
Score: 0.9666666666666667
Classes: [0 1 2]
获取各个特征的权重:[0.93420127 0.06579873]
附件一:手写推导过程练习



