【ML-3.1】梯度下降于牛顿法实例

目录

1. 案例
2. 完成代码
3. 执行结果截图
4. 实验总结分析
5. 对于实验的改进意见

一、案例

二、完成代码

 

%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from numpy import genfromtxt
dataPath = r"./Input/data1.csv"
dataSet = pd.read_csv(dataPath,header=None)
print(dataSet)
price = []
rooms = []
area = []
for data in range(0,len(dataSet)):
    area.append(dataSet[0][data])
    rooms.append(dataSet[1][data])
    price.append(dataSet[2][data])
#目标函数：导入参数为2个数组
def func(y_pre,y_true):
    s = 0
    for i in range(len(y_pre)):
        s += (y_pre[i]-y_true[i])**2
    return 0.5*s
#目标函数求导：导入参数为3个数组--梯度计算公式
def dfunc(y_pre,y_true,xi):
    s=0
    for i in range(len(y_pre)):
        s+= (y_pre[i]-y_true[i])*xi[i]
    return s

#梯度下降方式
def gradientDescent(rooms, price, area):
    #初始化三个值
    epochs = 500
    theta = 3*[1]  #分别为常熟，房子数量权值，面积权值赋初始值
    lr=3*[0.000000001]
    x0=5*[1]
    y_pre=5*[0]
    loss=[]
    for i in range(epochs):
        thetac = 3*[0]        #这个必须放到里面，第一次是放到外面，导致出现NAN
        for j in range(len(x0)):
            y_pre[j]=x0[j]*theta[0]+rooms[j]*theta[1]+area[j]*theta[2]
        #使用BGD方式更新梯度数据
        thetac[0] =dfunc(y_pre,price,x0)
        thetac[1] =dfunc(y_pre,price,rooms)
        thetac[2] =dfunc(y_pre,price,area)
        #更新权值数据
        theta = np.subtract(theta,np.multiply(lr,thetac))
        # 计算一次损失函数
        loss_one=func(y_pre,price)
        loss.append(loss_one)
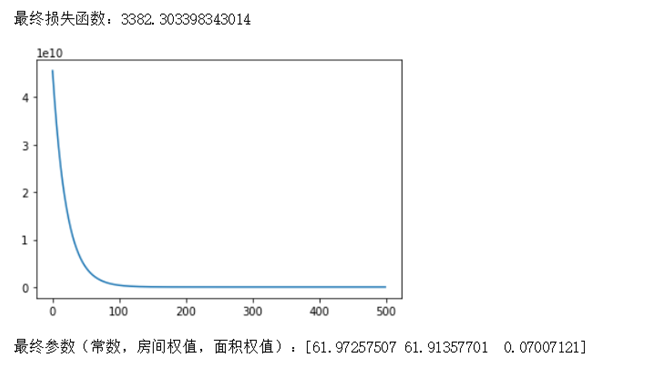
    print("最终损失函数：%s "%loss_one)
    plt.plot(loss)
    plt.show()
    return theta
result=gradientDescent(rooms, price, area)
print("最终参数（常数，房间权值，面积权值）：%s "%result)

 

　　

 

三、执行结果截图

四、实验总结分析

本文样本太少，代换100以后基本已经收敛，不能再进行优化了。这个和初始值有很大关联，因此建议对初始值进行筛选。

五、对于实验的改进意见

初始值选择：本文将数据拷贝到pycharm进行处理：代码如下：

 

# Author:yifan
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
area = [2104, 1600, 2400, 1416, 3000]
rooms = [3, 3, 3, 2, 4]
price = [400, 330, 369, 342, 540]

#目标函数：导入参数为2个数组
def func(y_pre,y_true):
    s = 0
    for i in range(len(y_pre)):
        s += (y_pre[i]-y_true[i])**2
    return 0.5*s

#目标函数求导：导入参数为3个数组--梯度计算公式
def dfunc(y_pre,y_true,xi):
    s=0
    for i in range(len(y_pre)):
        s+= (y_pre[i]-y_true[i])*xi[i]
    return s
#梯度下降方式
def gradientDescent(rooms, price, area,theta):
    #初始化三个值
    epochs = 500
    # theta = 3*[20]  #分别为常熟，房子数量权值，面积权值赋初始值
    lr=3*[0.000000001]
    x0=5*[1]
    y_pre=5*[0]
    loss=[]
    for i in range(epochs):
        thetac = 3*[0]        #这个必须放到里面，第一次是放到外面，导致出现NAN
        for j in range(len(x0)):
            y_pre[j]=x0[j]*theta[0]+rooms[j]*theta[1]+area[j]*theta[2]
        #使用BGD方式更新梯度数据
        thetac[0] =dfunc(y_pre,price,x0)
        thetac[1] =dfunc(y_pre,price,rooms)
        thetac[2] =dfunc(y_pre,price,area)
        #更新权值数据
        theta = np.subtract(theta,np.multiply(lr,thetac))
        # 计算一次损失函数
        loss_one=func(y_pre,price)
        loss.append(loss_one)
        # print(loss_one)
        if loss_one <  1000:
            break
    # plt.plot(loss)
    # plt.show()
    print(loss_one)
    return loss_one
result=[]
for i in range(80):
    theta = 3*[i]  #分别为常熟，房子数量权值，面积权值赋初始值
    result_one = gradientDescent(rooms, price, area,theta)
    result.append(result_one)
minLoss = min(result)
for i in range(80):
    if result[i]==minLoss:
        minLossIndex=i
print("最小的损失函数：%s,最小的时候的初始值：%s" %(minLoss,minLossIndex))

 

　　

 

结果如下:

因此再更改2代码中的初始值：theta = 3*[62]

六、牛顿法

1.解决思路

1.1牛顿法思路：

 

1.2 本题公式推导：

   

2.完成代码

 

def Newton_3(c , t):
    while abs(t * t * t - c) > 1e-6:
        t = t - (t*t*t-c)/(3*t*t)
        print(t)
    return t
print("牛顿法计算值：%s"%(Newton_3(2, 1)))
print("真实值：%s"%(2**(1/3)))

3.执行结果截图

4.实验总结分析：

使用牛顿法，通过观察，速度非常快，只经过了几次迭代便能完成，但是需要对数学公式进行导。