【ML-9-5】SVM的sklearn.svm.SVC()函数应用

经常用到sklearn中的SVC函数，这里把文档中的参数：

本身这个函数也是基于libsvm实现的，所以在参数设置上有很多相似的地方。（PS: libsvm中的二次规划问题的解决算法是SMO）。

sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma='auto', coef0=0.0, shrinking=True, probability=False,

Tol=0.001, cache_size200, class_weight=None, verbose=False,  max_iter=-1, 

decision_function_shape=None,random_state=None)

参数：

1、C：C-SVC的惩罚参数C默认值是1.0，C越大，相当于惩罚松弛变量，希望松弛变量接近0，即对误分类的惩罚增大，趋向于对训练集全分对的情况，这样对训练集测试时准确率很高，但泛化能力弱。C值小，对误分类的惩罚减小，允许容错，将他们当成噪声点，泛化能力较强。

C一般可以选择为：0.0001 到10000,选择的越大，表示对错误例惩罚程度越大，可能会导致模型过拟合

2、kernel ：核函数，默认是rbf，可以是'linear', 'poly', 'rbf', 'sigmoid', 'precomputed' 

  　　0 – 线性：u'v

 　　 1 – 多项式：(gamma*u'*v + coef0)^degree

  　　2 – RBF函数：exp(-gamma|u-v|^2)

  　　3 –sigmoid：tanh(gamma*u'*v + coef0)

数学表达式：

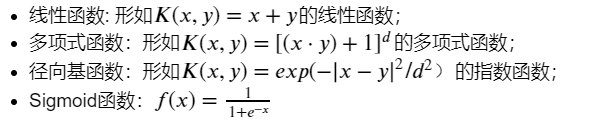
3、degree ：多项式poly函数的维度，默认是3，选择其他核函数时会被忽略。建议设置为2；

4、gamma ：'rbf'，'poly'和'sigmoid'的核系数。当前默认值为'auto'，它使用1 / n_features，如果gamma='scale'传递，则使用1 /（n_features * X.std（））作为gamma的值。当前默认的gamma''auto'将在版本0.22中更改为'scale'。

5、 coef0 ：核函数的常数项。对于'poly'和 'sigmoid'有用。

6、probability ：默认False。是否启用概率估计。必须在调用fit之前启用它，并且会减慢该方法的速度。

7、shrinking ：默认为true，是否采用shrinking heuristic（收缩启发式）方法

8、 tol ：默认为1e-3，停止训练的误差值大小，

9、cache_size ：默认为200，核函数cache缓存大小

10、 class_weight ：{dict，'balanced'}。将类i的参数C设置为SVC的class_weight [i] * C. 如果没有给出，所有类都应该有一个权重。"平衡"模式使用y的值自动调整与输入数据中的类频率成反比的权重n_samples / (n_classes * np.bincount(y))

11、verbose ：默认False。启用详细输出。请注意，此设置利用libsvm中的每进程运行时设置，如果启用，则可能无法在多线程上下文中正常运行。

12、max_iter ：最大迭代次数。-1为无限制。

13、decision_function_shape ：'ovo', 'ovr' or None, default=None3

14、random_state ：默认 无。伪随机数生成器的种子在对数据进行混洗以用于概率估计时使用。如果是int，则random_state是随机数生成器使用的种子; 如果是RandomState实例，则random_state是随机数生成器; 如果没有，随机数生成器所使用的RandomState实例np.random。

主要调节的参数有：C、kernel、degree、gamma、coef0。

   

与核函数相对应的libsvm参数建议：

1）对于线性核函数，没有专门需要设置的参数

2）对于多项式核函数，有三个参数。-d用来设置多项式核函数的最高此项次数，也就是公式中的d，默认值是3。-g用来设置核函数中的gamma参数设置，也就是公式中的第一个r(gamma)，默认值是1/k（k是类别数）。-r用来设置核函数中的coef0，也就是公式中的第二个r，默认值是0。

3）对于RBF核函数，有一个参数。-g用来设置核函数中的gamma参数设置，也就是公式中的第一个r(gamma)，默认值是1/k（k是类别数）。

4）对于sigmoid核函数，两个参数g以及r：gamma一般可选1 2 3 4，coef0选0.2 0.4 0.60.8 1

属性：

support_ ：支持向量索引。

support_vectors_ ：支持向量。

n_support_ ：每一类的支持向量数目

dual_coef_ ：决策函数中支持向量的系数

coef_ ：赋予特征的权重（原始问题中的系数）。这仅适用于线性内核。

intercept_ ：决策函数中的常量。

  

---实验练习

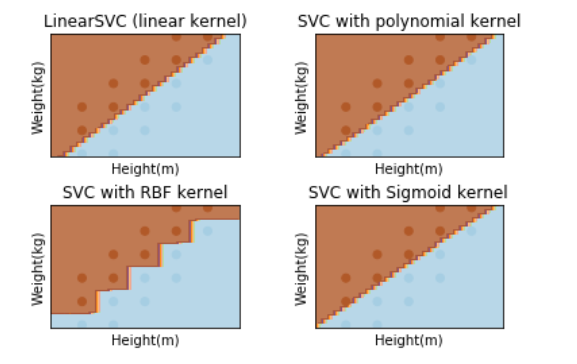
对身高体重的数据进行svm分类，要求分别使用线性函数、三次多项式函数、径向基函数和Sigmoid函数作为核函数进行模型训练，并观察分类效果(利用plt绘制样本点，胖的样本点与瘦的样本点用颜色区分，结果绘制出分类曲线)：

   

代码：

   

%matplotlib inline  
import numpy as np  
import scipy as sp  
from sklearn import svm
from sklearn.model_selection import train_test_split
# 注意: 如果sklearn是0.18之前的版本，则执行下面的语句：
# from sklearn.cross_validation import train_test_split  
import matplotlib.pyplot as plt  
#导入数据
data   = []  
labels = []  
# 读取身高体重数据集
with open("./Input/data.txt") as ifile:  
        for line in ifile:  
            tokens = line.strip().split(' ')  
            # data列表存储身高体重数据
            data.append([float(tk) for tk in tokens[:-1]]) 
            # label列表存储此人被定义为胖还是瘦
            labels.append(tokens[-1])  
# x: 以array形式存储身高体重构成的坐标
x = np.array(data)  
# labels: 将label列表array化
labels = np.array(labels)  
y = np.zeros(labels.shape) 
# y：存储0,1化的体重标签，值为0说明此人被定义为瘦，值为1说明此人定义为胖
y[labels=='fat']=1  
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.0)  
# 建立画布（可以不用关心具体的实现过程）
h = .02    
x_min, x_max = x_train[:, 0].min() - 0.1, x_train[:, 0].max() + 0.1  
y_min, y_max = x_train[:, 1].min() - 1, x_train[:, 1].max() + 1  
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),  
                     np.arange(y_min, y_max, h))  
# 绘图名称
titles = ['LinearSVC (linear kernel)',  
          'SVC with polynomial kernel',  
          'SVC with RBF kernel',  
          'SVC with Sigmoid kernel'] 

'''
svm.SVC(kernel='linear')：核函数为线性函数
svm.SVC(kernel='poly', degree=3)：核函数为3次多项式函数，如果degree=n，则使用的核函数是n次多项式函数
svm.SVC()：核函数为径向基函数
svm.SVC(kernel='sigmoid')：核函数为Sigmoid函数
'''
#以下是参数的重点部分：
# 核函数为线性函数
clf_linear  = svm.SVC(kernel='linear',C=50).fit(x, y)
# 核函数为多项式函数
clf_poly    = svm.SVC(kernel='poly', degree=2,coef0=10).fit(x, y)   
# 核函数为径向基函数
clf_rbf     = svm.SVC(kernel='rbf',C=100,gamma=0.5).fit(x, y)  
# 核函数为Sigmoid函数
clf_sigmoid = svm.SVC(kernel='sigmoid',C=1000000,gamma=0.0001,coef0=-1.5).fit(x, y)  

for i, clf in enumerate((clf_linear, clf_poly, clf_rbf, clf_sigmoid)):  
    answer = clf.predict(np.c_[xx.ravel(), yy.ravel()]) 
    plt.subplot(2, 2, i + 1)  
    plt.subplots_adjust(wspace=0.4, hspace=0.4)      
    # 将数据点绘制在坐标图上  
    z = answer.reshape(xx.shape)  
    plt.contourf(xx, yy, z, cmap=plt.cm.Paired, alpha=0.8)  
  
    plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train, cmap=plt.cm.Paired)  
    plt.xlabel('Height(m)')  
    plt.ylabel('Weight(kg)')  
    plt.xlim(xx.min(), xx.max())  
    plt.ylim(yy.min(), yy.max())  
    plt.xticks(())  
    plt.yticks(())  
    plt.title(titles[i])  
plt.show()  

实验结果：