「学习笔记」块状链表（STL）

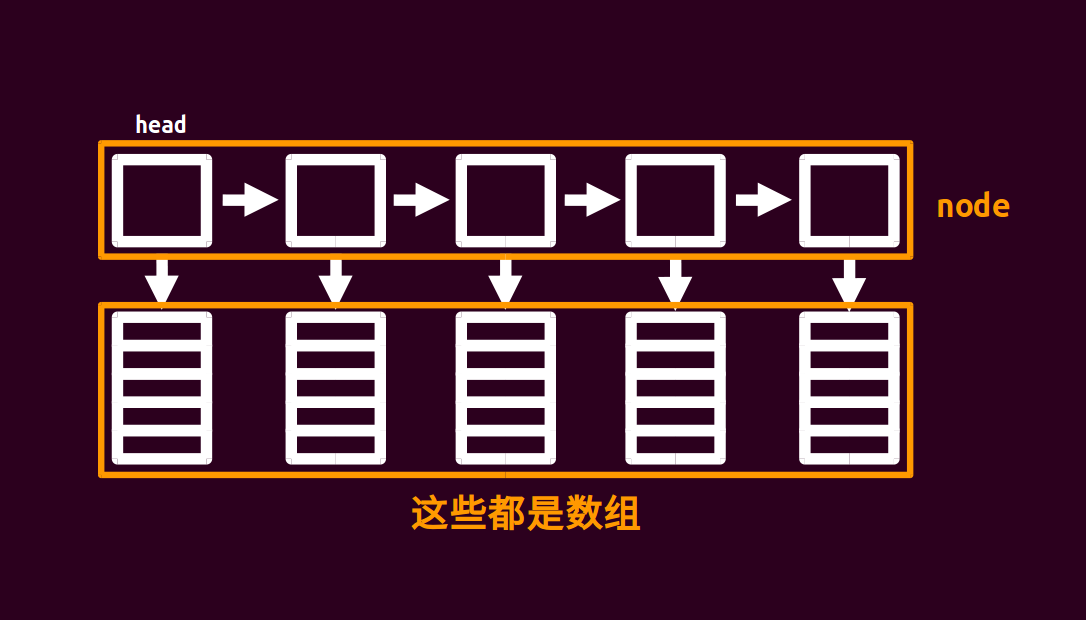
块状链表是一个集合了分块和链表的优秀数据结构。链表的每一个指针指向一个数组，每个数组的大小都接近 \(\sqrt{n}\)，因此块状链表的复杂度都为 \(\sqrt{n}\)。

大概长这样。（图片来自 \(\texttt{OI-Wiki}\)）

可以用它水过普通平衡树例题，所以又称为“五分钟平衡树”。

块状链表支持插入、分裂、查找等操作。

list<vector<ll>> List;

using lit = list<vector<ll>>::iterator;
using vit = vector<ll>::iterator;

基本操作

查找

遍历链表，来找到被查找元素的位置。

lit find(const int &p) {
    int cnt = 0;
    for (lit it = List.begin(); it != List.end(); ++ it) {
        if ((*it).back() >= p) {
            return it;
        }
    }
}

（插入）分裂

当一个数组的大小超过 \(2 \times \sqrt{n}\) 时，执行分裂操作以保证复杂度，否则就会退化成普通数组。

具体应该怎么做呢？在链表上新建一个节点和数组，将被分裂节点的后 \(\sqrt{n}\) 个值复制到新节点上，被分裂节点在删除后 \(\sqrt{n}\) 个值。

void insert(int x) {
    lit it = find(x);
    (*it).emplace(lower_bound((*it).begin(), (*it).end(), x), x);
    if ((*it).size() > lim) {
        List.emplace(next(it), (*it).begin() + (lim / 2), (*it).end());
        (*it).erase((*it).begin() + (lim / 2), (*it).end());
    }
}

删除

void erase(int x) {
    lit it = find(x);
    (*it).erase(lower_bound((*it).begin(), (*it).end(), x));
    if ((*it).empty()) {
        List.erase(it);
    }
}

例题

P3369 【模板】普通平衡树

// The code was written by yifan, and yifan is neutral!!!

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define bug puts("NOIP rp ++!");
#define rep(i, a, b, c) for (int i = (a); i <= (b); i += (c))
#define per(i, a, b, c) for (int i = (a); i >= (b); i -= (c))

template<typename T>
inline T read() {
    T x = 0;
    bool fg = 0;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        fg |= (ch == '-');
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    return fg ? ~x + 1 : x;
}

template<typename T>
void write(T x) {
    if (x < 0) {
        putchar('-');
        x = -x;
    }
    if (x > 9) {
        write(x / 10);
    }
    putchar(x % 10 + '0');
}

template<typename T>
void print(T x, char c) {
   write(x);
   putchar(c);
}

list<vector<ll>> List;

using lit = list<vector<ll>>::iterator;
using vit = vector<ll>::iterator;

int lim;

lit find(const int &p) {
    int cnt = 0;
    for (lit it = List.begin(); it != List.end(); ++ it) {
        if ((*it).back() >= p) {
            return it;
        }
    }
}

void insert(int x) {
    lit it = find(x);
    (*it).emplace(lower_bound((*it).begin(), (*it).end(), x), x);
    if ((*it).size() > lim) {
        List.emplace(next(it), (*it).begin() + (lim / 2), (*it).end());
        (*it).erase((*it).begin() + (lim / 2), (*it).end());
    }
}

void erase(int x) {
    lit it = find(x);
    (*it).erase(lower_bound((*it).begin(), (*it).end(), x));
    if ((*it).empty()) {
        List.erase(it);
    }
}

int kth(int k) {
    for (vector<ll> it : List) {
        if (it.size() >= k) {
            return it[k - 1];
        } else {
            k -= it.size();
        }
    }
    return 0;
}

int num(int x) {
    int cnt = 0;
    for (vector<ll> it : List) {
        if (it.back() >= x) {
            cnt += lower_bound(it.begin(), it.end(), x) - it.begin() + 1;
            return cnt;
        } else {
            cnt += it.size();
        }
    }
}

int qpre(int x) {
    lit it = find(x);
    vit it1 = lower_bound((*it).begin(), (*it).end(), x);
    if (it1 == (*it).begin()) {
        -- it;
        return (*it).back();
    } else {
        -- it1;
        return (*it1);
    }
}

int qnxt(int x) {
    lit it = find(x);
    vit it1 = upper_bound((*it).begin(), (*it).end(), x);
    if (it1 == (*it).end()) {
        ++ it;
        return (*it).front();
    } else {
        return *it1;
    }
}

int n;

int main() {
    vector<ll> tmp;
    tmp.emplace_back(LLONG_MAX);
    List.emplace_back(tmp);
    n = read<int>();
    lim = sqrt(n);
    for (int i = 1, op, x; i <= n; ++ i) {
        op = read<int>(), x = read<int>();
        if (op == 1) {
            insert(x);
        }
        if (op == 2) {
            erase(x);
        }
        if (op == 3) {
            print(num(x), '\n');
        }
        if (op == 4) {
            print(kth(x), '\n');
        }
        if (op == 5) {
            print(qpre(x), '\n');
        }
        if (op == 6) {
            print(qnxt(x), '\n');
        }
    }
    return 0;
}