「解题报告」CSP - S 2022
[CSP-S 2022] 假期计划
题目描述
小熊的地图上有 \(n\) 个点，其中编号为 \(1\) 的是它的家、编号为 \(2, 3, \ldots, n\) 的都是景点。部分点对之间有双向直达的公交线路。如果点 \(x\) 与 \(z_1\)、\(z_1\) 与 \(z_2\)、……、\(z_{k - 1}\) 与 \(z_k\)、\(z_k\) 与 \(y\) 之间均有直达的线路，那么我们称 \(x\) 与 \(y\) 之间的行程可转车 \(k\) 次通达；特别地，如果点 \(x\) 与 \(y\) 之间有直达的线路，则称可转车 \(0\) 次通达。
很快就要放假了，小熊计划从家出发去 \(4\) 个不同的景点游玩，完成 \(5\) 段行程后回家：家 \(\to\) 景点 A \(\to\) 景点 B \(\to\) 景点 C \(\to\) 景点 D \(\to\) 家且每段行程最多转车 \(k\) 次。转车时经过的点没有任何限制，既可以是家、也可以是景点，还可以重复经过相同的点。例如，在景点 A \(\to\) 景点 B 的这段行程中，转车时经过的点可以是家、也可以是景点 C，还可以是景点 D \(\to\) 家这段行程转车时经过的点。
假设每个景点都有一个分数，请帮小熊规划一个行程，使得小熊访问的四个不同景点的分数之和最大。
输入格式
第一行包含三个正整数 \(n, m, k\)，分别表示地图上点的个数、双向直达的点对数量、每段行程最多的转车次数。
第二行包含 \(n - 1\) 个正整数，分别表示编号为 \(2, 3, \ldots, n\) 的景点的分数。
接下来 \(m\) 行，每行包含两个正整数 \(x, y\)，表示点 \(x\) 和 \(y\) 之间有道路直接相连，保证 \(1 \le x, y \le n\)，且没有重边，自环。
输出格式
输出一个正整数，表示小熊经过的 \(4\) 个不同景点的分数之和的最大值。
样例 #1
样例输入 #1
8 8 1
9 7 1 8 2 3 6
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 1
样例输出 #1
27
样例 #2
样例输入 #2
7 9 0
1 1 1 2 3 4
1 2
2 3
3 4
1 5
1 6
1 7
5 4
6 4
7 4
样例输出 #2
7
提示
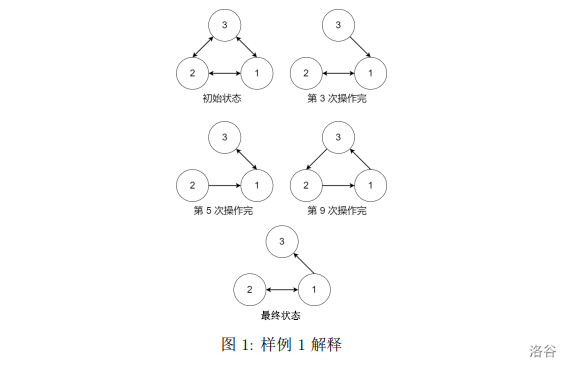
【样例解释 #1】
当计划的行程为 \(1 \to 2 \to 3 \to 5 \to 7 \to 1\) 时，\(4\) 个景点的分数之和为 \(9 + 7 + 8 + 3 = 27\)，可以证明其为最大值。
行程 \(1 \to 3 \to 5 \to 7 \to 8 \to 1\) 的景点分数之和为 \(24\)、行程 \(1 \to 3 \to 2 \to 8 \to 7 \to 1\) 的景点分数之和为 \(25\)。它们都符合要求，但分数之和不是最大的。
行程 \(1 \to 2 \to 3 \to 5 \to 8 \to 1\) 的景点分数之和为 \(30\)，但其中 \(5 \to 8\) 至少需要转车 \(2\) 次，因此不符合最多转车 \(k = 1\) 次的要求。
行程 \(1 \to 2 \to 3 \to 2 \to 3 \to 1\) 的景点分数之和为 \(32\)，但游玩的并非 \(4\) 个不同的景点，因此也不符合要求。
【样例 #3】
见附件中的 holiday/holiday3.in 与 holiday/holiday3.ans。
【数据范围】
对于所有数据，保证 \(5 \le n \le 2500\)，\(1 \le m \le 10000\)，\(0 \le k \le 100\)，所有景点的分数 \(1 \le s_i \le {10}^{18}\)。保证至少存在一组符合要求的行程。
| 测试点编号 | \(n \le\) | \(m \le\) | \(k \le\) |
|---|---|---|---|
| \(1 \sim 3\) | \(10\) | \(20\) | \(0\) |
| \(4 \sim 5\) | \(10\) | \(20\) | \(5\) |
| \(6 \sim 8\) | \(20\) | \(50\) | \(100\) |
| \(9 \sim 11\) | \(300\) | \(1000\) | \(0\) |
| \(12 \sim 14\) | \(300\) | \(1000\) | \(100\) |
| \(15 \sim 17\) | \(2500\) | \(10000\) | \(0\) |
| \(18 \sim 20\) | \(2500\) | \(10000\) | \(100\) |
预处理出每个点附近离家近（可直接从家到到达的地方）且点的权值最大的点，点的个数控制在 \(\le 3\) 即可，将这些点放入集合 \(s\) 中。
先枚举 \(b, c\)，在确保 \(b, c\) 可以互相到达的情况下，再通过 \(s_b\) 来枚举 \(a\)，通过 \(s_c\) 来枚举 \(d\)，最后再判断 \(a, b, c, d\) 是否有重复，没有重复则进行答案的比较和更新即可。
//The code was written by yifan, and yifan is neutral!!!
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define bug puts("NOIP rp ++!");
#define rep(i, a, b, c) for (int i = (a); i <= (b); i += (c))
#define per(i, a, b, c) for (int i = (a); i >= (b); i -= (c))
template<typename T>
inline T read() {
T x = 0;
bool fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? ~x + 1 : x;
}
const int N = 2510;
int n, m, k;
ll s[N], dis[N];
vector<int> e[N];
bool ok[N][N];
vector<int> _s[N];
void bfs(int x) {
rep (i, 1, n, 1) {
dis[i] = -1;
}
queue<int> q;
q.emplace(x);
dis[x] = 0;
while (!q.empty()) {
int u = q.front();
q.pop();
if (u != x) {
ok[x][u] = 1;
if (x != 1 && ok[1][u]) {
_s[x].emplace_back(u);
sort(_s[x].begin(), _s[x].end(), [](int x, int y) {
return s[x] > s[y];
});
}
if (_s[x].size() > 3) {
_s[x].pop_back();
}
}
if (dis[u] == k + 1) continue ;
for (int v : e[u]) {
if (dis[v] == -1) {
dis[v] = dis[u] + 1;
q.emplace(v);
}
}
}
}
int main() {
n = read<int>(), m = read<int>(), k = read<int>();
rep (i, 2, n, 1) {
s[i] = read<ll>();
}
int x, y;
rep (i, 1, m, 1) {
x = read<int>(), y = read<int>();
e[x].emplace_back(y);
e[y].emplace_back(x);
}
rep (i, 1, n, 1) {
bfs(i);
}
ll ans = 0;
rep (b, 2, n, 1) {
rep (c, 2, n, 1) {
if (!ok[b][c]) continue ;
for (int a : _s[b]) {
for (int d : _s[c]) {
if (a != d && a != c && d != b) {
ans = max(ans, s[a] + s[b] + s[c] + s[d]);
}
}
}
}
}
cout << ans << '\n';
return 0;
}
[CSP-S 2022] 策略游戏
题目描述
小 L 和小 Q 在玩一个策略游戏。
有一个长度为 \(n\) 的数组 \(A\) 和一个长度为 \(m\) 的数组 \(B\)，在此基础上定义一个大小为 \(n \times m\) 的矩阵 \(C\)，满足 \(C_{i j} = A_i \times B_j\)。所有下标均从 \(1\) 开始。
游戏一共会进行 \(q\) 轮，在每一轮游戏中，会事先给出 \(4\) 个参数 \(l_1, r_1, l_2, r_2\)，满足 \(1 \le l_1 \le r_1 \le n\)、\(1 \le l_2 \le r_2 \le m\)。
游戏中，小 L 先选择一个 \(l_1 \sim r_1\) 之间的下标 \(x\)，然后小 Q 选择一个 \(l_2 \sim r_2\) 之间的下标 \(y\)。定义这一轮游戏中二人的得分是 \(C_{x y}\)。
小 L 的目标是使得这个得分尽可能大，小 Q 的目标是使得这个得分尽可能小。同时两人都是足够聪明的玩家，每次都会采用最优的策略。
请问：按照二人的最优策略，每轮游戏的得分分别是多少？
输入格式
第一行输入三个正整数 \(n, m, q\)，分别表示数组 \(A\)，数组 \(B\) 的长度和游戏轮数。
第二行：\(n\) 个整数，表示 \(A_i\)，分别表示数组 \(A\) 的元素。
第三行：\(m\) 个整数，表示 \(B_i\)，分别表示数组 \(B\) 的元素。
接下来 \(q\) 行，每行四个正整数，表示这一次游戏的 \(l_1, r_1, l_2, r_2\)。
输出格式
输出共 \(q\) 行，每行一个整数，分别表示每一轮游戏中，小 L 和小 Q 在最优策略下的得分。
样例 #1
样例输入 #1
3 2 2
0 1 -2
-3 4
1 3 1 2
2 3 2 2
样例输出 #1
0
4
样例 #2
样例输入 #2
6 4 5
3 -1 -2 1 2 0
1 2 -1 -3
1 6 1 4
1 5 1 4
1 4 1 2
2 6 3 4
2 5 2 3
样例输出 #2
0
-2
3
2
-1
提示
【样例解释 #1】
这组数据中，矩阵 \(C\) 如下：
在第一轮游戏中，无论小 L 选取的是 \(x = 2\) 还是 \(x = 3\)，小 Q 都有办法选择某个 \(y\) 使得最终的得分为负数。因此小 L 选择 \(x = 1\) 是最优的，因为这样得分一定为 \(0\)。
而在第二轮游戏中，由于小 L 可以选 \(x = 2\)，小 Q 只能选 \(y = 2\)，如此得分为 \(4\)。
【样例 #3】
见附件中的 game/game3.in 与 game/game3.ans。
【样例 #4】
见附件中的 game/game4.in 与 game/game4.ans。
【数据范围】
对于所有数据，\(1 \le n, m, q \le {10}^5\)，\(-{10}^9 \le A_i, B_i \le {10}^9\)。对于每轮游戏而言，\(1 \le l_1 \le r_1 \le n\)，\(1 \le l_2 \le r_2 \le m\)。
| 测试点编号 | \(n, m, q \le\) | 特殊条件 |
|---|---|---|
| \(1\) | \(200\) | 1, 2 |
| \(2\) | \(200\) | 1 |
| \(3\) | \(200\) | 2 |
| \(4 \sim 5\) | \(200\) | 无 |
| \(6\) | \(1000\) | 1, 2 |
| \(7 \sim 8\) | \(1000\) | 1 |
| \(9 \sim 10\) | \(1000\) | 2 |
| \(11 \sim 12\) | \(1000\) | 无 |
| \(13\) | \({10}^5\) | 1, 2 |
| \(14 \sim 15\) | \({10}^5\) | 1 |
| \(16 \sim 17\) | \({10}^5\) | 2 |
| \(18 \sim 20\) | \({10}^5\) | 无 |
其中，特殊性质 1 为：保证 \(A_i, B_i > 0\)。
特殊性质 2 为：保证对于每轮游戏而言，要么 \(l_1 = r_1\)，要么 \(l_2 = r_2\)。
我的做法是分类讨论了 \(9\) 种情况。
-
\(A, B\) 全为正数，答案是 \(A_{\max} \times B_{\max}\)。
-
\(A\) 全是负数，\(B\) 全是正数，答案是 \(A_{\max} \times B_{\max}\)。
-
\(A\) 全是正数，\(B\) 全是负数，答案是 \(A_{\min} \times B_{\min}\)。
-
\(A, B\) 全是负数，答案是 \(A_{\min} \times B_{\max}\)。
-
\(A\) 有正有负，\(B\) 全是正数，答案是 \(A_{\max} \times B_{\min}\)。
-
\(A\) 有正有负，\(B\) 全是负数，答案是 \(\max\left \{ \left (+ \right )A_{\min} \times B_{\min}, \left (- \right )A_{\min} \times B_{\max} \right \}\)。
-
\(A\) 全是正数，\(B\) 有正有负，答案是 \(A_{\min} \times B_{\min}\)。
-
\(A\) 全是负数，\(B\) 有正有负，答案是 \(A_{\max} \times B_{\max}\)。
-
\(A, B\) 均有正有负，答案为 \(\max\{(-)A_{\max} \times B_{\max}, (+)A_{\min} \times B_{\min} \}\)。
然后用线段树进行维护即可。
//The code was written by yifan, and yifan is neutral!!!
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define bug puts("NOIP rp ++!");
#define rep(i, a, b, c) for (int i = (a); i <= (b); i += (c))
#define per(i, a, b, c) for (int i = (a); i >= (b); i -= (c))
template<typename T>
inline T read() {
T x = 0;
bool fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? ~x + 1 : x;
}
const int N = 1e5 + 5;
using ask = tuple<int, int, int, int>;
int n, m, q;
bool xz1 = 1, xz2 = 1;
int lg[N];
ll a[N], b[N];
ll sta_max[N][20], sta_min[N][20], stb_max[N][20], stb_min[N][20];
vector<ask> Q;
#define ls (u << 1)
#define rs (u << 1 | 1)
struct seg {
ll val1, val0;
} t[N << 2];
void pushup(int u) {
t[u].val1 = min(t[ls].val1, t[rs].val1);
t[u].val0 = max(t[ls].val0, t[rs].val0);
}
void build(int u, int l, int r) {
if (l == r) {
if (a[l] > 0) {
t[u].val1 = a[l];
t[u].val0 = -1e9;
} else if (a[l] == 0) {
t[u].val1 = t[u].val0 = 0;
} else {
t[u].val0 = a[l];
t[u].val1 = 1e9;
}
return ;
}
int mid = (l + r) >> 1;
build(ls, l, mid);
build(rs, mid + 1, r);
pushup(u);
}
int query_fu(int u, int l, int r, int lr, int rr) {
if (lr <= l && r <= rr) {
return t[u].val0;
}
int mid = (l + r) >> 1;
ll val1 = -1e9, val2 = -1e9;
if (lr <= mid) {
val1 = query_fu(ls, l, mid, lr, rr);
}
if (rr > mid) {
val2 = query_fu(rs, mid + 1, r, lr, rr);
}
return max(val1, val2);
}
int query_zh(int u, int l, int r, int lr, int rr) {
if (lr <= l && r <= rr) {
return t[u].val1;
}
int mid = (l + r) >> 1;
ll val1 = 1e9, val2 = 1e9;
if (lr <= mid) {
val1 = query_zh(ls, l, mid, lr, rr);
}
if (rr > mid) {
val2 = query_zh(rs, mid + 1, r, lr, rr);
}
return min(val1, val2);
}
int st_ask(int l, int r, int** st, bool mxn) {
int g = lg[r - l + 1];
if (mxn) {
return max(st[l][g], st[r - (1 << g) + 1][g]);
} else {
return min(st[l][g], st[r - (1 << g) + 1][g]);
}
return 0;
}
void solve1() {
int l_1, r_1, l_2, r_2;
ll maxx, minn, da, db;
for (ask it : Q) {
tie(l_1, r_1, l_2, r_2) = it;
da = lg[r_1 - l_1 + 1];
db = lg[r_2 - l_2 + 1];
maxx = max(sta_max[l_1][da], sta_max[r_1 - (1 << da) + 1][da]);
minn = min(stb_min[l_2][db], stb_min[r_2 - (1 << db) + 1][db]);
cout << maxx * minn << '\n';
}
}
void solve2() {
int l_1, r_1, l_2, r_2;
ll val, g;
for (ask it : Q) {
tie(l_1, r_1, l_2, r_2) = it;
if (l_1 == r_1) {
g = lg[r_2 - l_2 + 1];
if (a[l_1] > 0) {
val = min(stb_min[l_2][g], stb_min[r_2 - (1 << g) + 1][g]);
} else {
val = max(stb_max[l_2][g], stb_max[r_2 - (1 << g) + 1][g]);
}
cout << a[l_1] * val << '\n';
} else {
g = lg[r_1 - l_1 + 1];
if (b[l_2] > 0) {
val = max(sta_max[l_1][g], sta_max[r_1 - (1 << g) + 1][g]);
} else {
val = min(sta_min[l_1][g], sta_min[r_1 - (1 << g) + 1][g]);
}
cout << b[l_2] * val << '\n';
}
}
}
int main() {
n = read<int>(), m = read<int>(), q = read<int>();
lg[0] = -1;
rep (i, 1, n, 1) {
a[i] = read<int>();
xz1 &= (a[i] > 0);
}
rep (i, 1, m, 1) {
b[i] = read<int>();
xz1 &= (b[i] > 0);
}
rep (i, 1, n, 1) {
sta_max[i][0] = a[i];
sta_min[i][0] = a[i];
}
rep (i, 1, max(n, m), 1) {
lg[i] = lg[i >> 1] + 1;
}
rep (j, 1, 19, 1) {
int k;
rep (i, 1, n, 1) {
k = i + (1 << j) - 1;
if (k > n) break ;
sta_max[i][j] = max(sta_max[i][j - 1], sta_max[i + (1 << (j - 1))][j - 1]);
sta_min[i][j] = min(sta_min[i][j - 1], sta_min[i + (1 << (j - 1))][j - 1]);
}
}
rep (i, 1, m, 1) {
stb_min[i][0] = b[i];
stb_max[i][0] = b[i];
}
rep (j, 1, 19, 1) {
int k;
rep (i, 1, m, 1) {
k = i + (1 << j) - 1;
if (k > m) break ;
stb_max[i][j] = max(stb_max[i][j - 1], stb_max[i + (1 << (j - 1))][j - 1]);
stb_min[i][j] = min(stb_min[i][j - 1], stb_min[i + (1 << (j - 1))][j - 1]);
}
}
int l_1, r_1, l_2, r_2;
rep (i, 1, q, 1) {
l_1 = read<int>(), r_1 = read<int>();
l_2 = read<int>(), r_2 = read<int>();
Q.emplace_back(l_1, r_1, l_2, r_2);
xz2 &= ((l_1 == r_1) || (l_2 == r_2));
}
if (xz1) {
solve1();
return 0;
}
if (xz2) {
solve2();
return 0;
}
build(1, 1, n);
for (ask it : Q) {
tie(l_1, r_1, l_2, r_2) = it;
ll mina = min(sta_min[l_1][lg[r_1 - l_1 + 1]], sta_min[r_1 - (1 << lg[r_1 - l_1 + 1]) + 1][lg[r_1 - l_1 + 1]]);
ll maxa = max(sta_max[l_1][lg[r_1 - l_1 + 1]], sta_max[r_1 - (1 << lg[r_1 - l_1 + 1]) + 1][lg[r_1 - l_1 + 1]]);
ll minb = min(stb_min[l_2][lg[r_2 - l_2 + 1]], stb_min[r_2 - (1 << lg[r_2 - l_2 + 1]) + 1][lg[r_2 - l_2 + 1]]);
ll maxb = max(stb_max[l_2][lg[r_2 - l_2 + 1]], stb_max[r_2 - (1 << lg[r_2 - l_2 + 1]) + 1][lg[r_2 - l_2 + 1]]);
if (mina >= 0) {
if (minb >= 0) {
cout << maxa * minb << '\n';
continue ;
}
if (maxb <= 0) {
cout << mina * minb << '\n';
continue ;
}
if (minb <= 0 && maxb >= 0) {
cout << mina * minb << '\n';
continue ;
}
}
if (maxa <= 0) {
if (minb >= 0) {
cout << maxa * maxb << '\n';
continue ;
}
if (maxb <= 0) {
cout << mina * maxb << '\n';
continue ;
}
if (minb <= 0 && maxb >= 0) {
cout << maxa * maxb << '\n';
continue ;
}
}
if (mina <= 0 && maxa >= 0) {
if (minb >= 0) {
cout << maxa * minb << '\n';
continue ;
}
if (maxb <= 0) {
if (mina <= 0) {
cout << mina * maxb << '\n';
} else {
cout << mina * minb << '\n';
}
}
if (minb <= 0 && maxb >= 0) {
ll val0 = query_fu(1, 1, n, l_1, r_1);
ll val1 = query_zh(1, 1, n, l_1, r_1);
cout << max(val0 * maxb, val1 * minb) << '\n';
}
}
}
return 0;
}
[CSP-S 2022] 星战
题目描述
在这一轮的星际战争中，我方在宇宙中建立了 \(n\) 个据点，以 \(m\) 个单向虫洞连接。我们把终点为据点 \(u\) 的所有虫洞归为据点 \(u\) 的虫洞。
战火纷飞之中这些虫洞很难长久存在，敌人的打击随时可能到来。这些打击中的有效打击可以分为两类：
- 敌人会摧毁某个虫洞，这会使它连接的两个据点无法再通过这个虫洞直接到达，但这样的打击无法摧毁它连接的两个据点。
- 敌人会摧毁某个据点，由于虫洞的主要技术集中在出口处，这会导致该据点的所有还未被摧毁的虫洞被一同摧毁。而从这个据点出发的虫洞则不会摧毁。
注意：摧毁只会导致虫洞不可用，而不会消除它的存在。
为了抗击敌人并维护各部队和各据点之间的联系，我方发展出了两种特种部队负责修复虫洞：
- A 型特种部队则可以将某个特定的虫洞修复。
- B 型特种部队可以将某据点的所有损坏的虫洞修复。
考虑到敌人打击的特点，我方并未在据点上储备过多的战略物资。因此只要这个据点的某一条虫洞被修复，处于可用状态，那么这个据点也是可用的。
我方掌握了一种苛刻的空间特性，利用这一特性我方战舰可以沿着虫洞瞬移到敌方阵营，实现精确打击。
为了把握发动反攻的最佳时机，指挥部必须关注战场上的所有变化，为了寻找一个能够进行反攻的时刻。总指挥认为：
- 如果从我方的任何据点出发，在选择了合适的路线的前提下，可以进行无限次的虫洞穿梭（可以多次经过同一据点或同一虫洞），那么这个据点就可以实现反击。
- 为了使虫洞穿梭的过程连续，尽量减少战舰在据点切换虫洞时的质能损耗，当且仅当只有一个从该据点出发的虫洞可用时，这个据点可以实现连续穿梭。
- 如果我方所有据点都可以实现反击，也都可以实现连续穿梭，那么这个时刻就是一个绝佳的反攻时刻。
总司令为你下达命令，要求你根据战场上实时反馈的信息，迅速告诉他当前的时刻是否能够进行一次反攻。
输入格式
输入的第一行包含两个正整数 \(n,m\)。
接下来 \(m\) 行每行两个数 \(u,v\)，表示一个从据点 \(u\) 出发到据点 \(v\) 的虫洞。保证 \(u \ne v\)，保证不会有两条相同的虫洞。初始时所有的虫洞和据点都是完好的。
接下来一行一个正整数 \(q\) 表示询问个数。
接下来 \(q\) 行每行表示一次询问或操作。首先读入一个正整数 \(t\) 表示指令类型：
- 若 \(t = 1\)，接下来两个整数 \(u, v\) 表示敌人摧毁了从据点 \(u\) 出发到据点 \(v\) 的虫洞。保证该虫洞存在且未被摧毁。
- 若 \(t = 2\)，接下来一个整数 \(u\) 表示敌人摧毁了据点 \(u\)。如果该据点的虫洞已全部被摧毁，那么这次袭击不会有任何效果。
- 若 \(t = 3\)，接下来两个整数 \(u, v\) 表示我方修复了从据点 \(u\) 出发到据点 \(v\) 的虫洞。保证该虫洞存在且被摧毁。
- 若 \(t = 4\)，接下来一个整数 \(u\) 表示我方修复了据点 \(u\)。如果该据点没有被摧毁的虫洞，那么这次修复不会有任何效果。
在每次指令执行之后，你需要判断能否进行一次反攻。如果能则输出 YES 否则输出 NO。
输出格式
输出一共 \(q\) 行。对于每个指令，输出这个指令执行后能否进行反攻。
样例 #1
样例输入 #1
3 6
2 3
2 1
1 2
1 3
3 1
3 2
11
1 3 2
1 2 3
1 1 3
1 1 2
3 1 3
3 3 2
2 3
1 3 1
3 1 3
4 2
1 3 2
样例输出 #1
NO
NO
YES
NO
YES
NO
NO
NO
YES
NO
NO
提示
【样例解释 #1】
虫洞状态可以参考下面的图片, 图中的边表示存在且未被摧毁的虫洞：
【样例 #2】
见附件中的 galaxy/galaxy2.in 与 galaxy/galaxy2.ans。
【样例 #3】
见附件中的 galaxy/galaxy3.in 与 galaxy/galaxy3.ans。
【样例 #4】
见附件中的 galaxy/galaxy4.in 与 galaxy/galaxy4.ans。
【数据范围】
对于所有数据保证：\(1 \le n \le 5 \times {10}^5\)，\(1 \le m \le 5 \times {10}^5\)，\(1 \le q \le 5 \times {10}^5\)。
| 测试点 | \(n \le\) | \(m \le\) | \(q \le\) | 特殊限制 |
|---|---|---|---|---|
| \(1 \sim 3\) | \(10\) | \(20\) | \(50\) | 无 |
| \(4 \sim 8\) | \({10}^3\) | \({10}^4\) | \({10}^3\) | 无 |
| \(9 \sim 10\) | \(5 \times {10}^5\) | \(5 \times {10}^5\) | \(5 \times {10}^5\) | 保证没有 \(t = 2\) 和 \(t = 4\) 的情况 |
| \(11 \sim 12\) | \(5 \times {10}^5\) | \(5 \times {10}^5\) | \(5 \times {10}^5\) | 保证没有 \(t = 4\) 的情况 |
| \(13 \sim 16\) | \({10}^5\) | \(5 \times {10}^5\) | \(5 \times {10}^5\) | 无 |
| \(17 \sim 20\) | \(5 \times {10}^5\) | \(5\times 10^5\) | \(5 \times {10}^5\) | 无 |
我们给每个点随机一个数值，以代替它的出度，如果最后的总出度等于所有点的数值和，那么说明每个点的出度都为 \(1\)，即有环。
//The code was written by yifan, and yifan is neutral!!!
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define bug puts("NOIP rp ++!");
#define rep(i, a, b, c) for (int i = (a); i <= (b); i += (c))
#define per(i, a, b, c) for (int i = (a); i >= (b); i -= (c))
typedef pair<int, int> pii;
template<typename T>
inline T read() {
T x = 0;
bool fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? ~x + 1 : x;
}
const int M = 5e5 + 5;
int n, m, q, tot, ans;
int s[M], w[M], cur[M];
inline ll read() {
ll x = 0;
int fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? ~x + 1 : x;
}
int main() {
mt19937 myrand(time(0));
n = read();
m = read();
rep (i, 1, n, 1) {
w[i] = myrand();
tot += w[i];
}
int a, b;
rep (i, 1, m, 1) {
a = read(), b = read();
s[b] += w[a];
cur[b] += w[a];
ans += w[a];
}
q = read();
int op;
rep (i, 1, q, 1) {
op = read();
if (op == 1) {
int u = read(), v = read();
cur[v] -= w[u];
ans -= w[u];
}
if (op == 2) {
int v = read();
ans -= cur[v];
cur[v] = 0;
}
if (op == 3) {
int u = read(), v = read();
cur[v] += w[u];
ans += w[u];
}
if (op == 4) {
int v = read();
ans += s[v] - cur[v];
cur[v] = s[v];
}
if (ans != tot) {
puts("NO");
} else {
puts("YES");
}
}
return 0;
}
[CSP-S 2022] 数据传输
题目背景
请勿滥用本题评测，违者可能处以封号处罚。
题目描述
小 C 正在设计计算机网络中的路由系统。
测试用的网络总共有 \(n\) 台主机，依次编号为 \(1 \sim n\)。这 \(n\) 台主机之间由 \(n - 1\) 根网线连接，第 \(i\) 条网线连接个主机 \(a_i\) 和 \(b_i\)。保证任意两台主机可以通过有限根网线直接或者间接地相连。受制于信息发送的功率，主机 \(a\) 能够直接将信息传输给主机 \(b\) 当且仅当两个主机在可以通过不超过 \(k\) 根网线直接或者间接的相连。
在计算机网络中，数据的传输往往需要通过若干次转发。假定小 C 需要将数据从主机 \(a\) 传输到主机 \(b\)（\(a \neq b\)），则其会选择出若干台用于传输的主机 \(c_1 = a, c_2, \ldots, c_{m - 1}, c_m = b\)，并按照如下规则转发：对于所有的 \(1 \le i < m\)，主机 \(c_i\) 将信息直接发送给 \(c_{i + 1}\)。
每台主机处理信息都需要一定的时间，第 \(i\) 台主机处理信息需要 \(v_i\) 单位的时间。数据在网络中的传输非常迅速，因此传输的时间可以忽略不计。据此，上述传输过程花费的时间为 \(\sum_{i = 1}^{m} v_{c_i}\)。
现在总共有 \(q\) 次数据发送请求，第 \(i\) 次请求会从主机 \(s_i\) 发送数据到主机 \(t_i\)。小 C 想要知道，对于每一次请求至少需要花费多少单位时间才能完成传输。
输入格式
输入的第一行包含三个正整数 \(n, Q, k\)，分别表示网络主机个数，请求个数，传输参数。数据保证 \(1 \le n \le 2 \times {10}^5\)，\(1 \le Q \le 2 \times {10}^5\)，\(1 \le k \le 3\)。
输入的第二行包含 \(n\) 个正整数，第 \(i\) 个正整数表示 \(v_i\)，保证 \(1 \le v_i \le {10}^9\)。
接下来 \(n - 1\) 行，第 \(i\) 行包含两个正整数 \(a_i, b_i\)，表示一条连接主机 \(a_i, b_i\) 的网线。保证 \(1 \le a_i, b_i \le n\)。
接下来 \(Q\) 行，第 \(i\) 行包含两个正整数 \(s_i, t_i\)，表示一次从主机 \(s_i\) 发送数据到主机 \(t_i\) 的请求。保证 \(1 \le s_i, t_i \le n\)，\(s_i \ne t_i\)。
输出格式
\(Q\) 行，每行一个正整数，表示第 \(i\) 次请求在传输的时候至少需要花费多少单位的时间。
样例 #1
样例输入 #1
7 3 3
1 2 3 4 5 6 7
1 2
1 3
2 4
2 5
3 6
3 7
4 7
5 6
1 2
样例输出 #1
12
12
3
提示
【样例解释 #1】
对于第一组请求，由于主机 \(4, 7\) 之间需要至少 \(4\) 根网线才能连接，因此数据无法在两台主机之间直接传输，其至少需要一次转发；我们让其在主机 \(1\) 进行一次转发，不难发现主机 \(1\) 和主机 \(4, 7\) 之间都只需要两根网线即可连接，且主机 \(1\) 的数据处理时间仅为 \(1\)，为所有主机中最小，因此最少传输的时间为 \(4 + 1 + 7 = 12\)。
对于第三组请求，由于主机 \(1, 2\) 之间只需要 \(1\) 根网线就能连接，因此数据直接传输就是最优解，最少传输的时间为 \(1 + 2 = 3\)。
【样例 #2】
见附件中的 transmit/transmit2.in 与 transmit/transmit2.ans。
该样例满足测试点 \(2\) 的限制。
【样例 #3】
见附件中的 transmit/transmit3.in 与 transmit/transmit3.ans。
该样例满足测试点 \(3\) 的限制。
【样例 #4】
见附件中的 transmit/transmit4.in 与 transmit/transmit4.ans。
该样例满足测试点 \(20\) 的限制。
【数据范围】
对于所有的测试数据，满足 \(1 \le n \le 2 \times {10}^5\)，\(1 \le Q \le 2 \times {10}^5\)，\(1 \le k \le 3\)，\(1 \le a_i, b_i \le n\)，\(1 \le s_i, t_i \le n\)，\(s_i \ne t_i\)。
| 测试点 | \(n \le\) | \(Q \le\) | \(k =\) | 特殊性质 |
|---|---|---|---|---|
| \(1\) | \(10\) | \(10\) | \(2\) | 是 |
| \(2\) | \(10\) | \(10\) | \(3\) | 是 |
| \(3\) | \(200\) | \(200\) | \(2\) | 是 |
| \(4 \sim 5\) | \(200\) | \(200\) | \(3\) | 是 |
| \(6 \sim 7\) | \(2000\) | \(2000\) | \(1\) | 否 |
| \(8 \sim 9\) | \(2000\) | \(2000\) | \(2\) | 否 |
| \(10 \sim 11\) | \(2000\) | \(2000\) | \(3\) | 否 |
| \(12 \sim 13\) | \(2 \times {10}^5\) | \(2 \times {10}^5\) | \(1\) | 否 |
| \(14\) | \(5 \times {10}^4\) | \(5 \times {10}^4\) | \(2\) | 是 |
| \(15 \sim 16\) | \({10}^5\) | \({10}^5\) | \(2\) | 是 |
| \(17 \sim 19\) | \(2 \times {10}^5\) | \(2 \times {10}^5\) | \(2\) | 否 |
| \(20\) | \(5 \times {10}^4\) | \(5 \times {10}^4\) | \(3\) | 是 |
| \(21 \sim 22\) | \({10}^5\) | \({10}^5\) | \(3\) | 是 |
| \(23 \sim 25\) | \(2 \times {10}^5\) | \(2 \times {10}^5\) | \(3\) | 否 |
特殊性质：保证 \(a_i = i + 1\)，而 \(b_i\) 则从 \(1, 2, \ldots, i\) 中等概率选取。
这个题就只有 \(16\) 分，算是最难的题了，只拿满前面的暴力分就已经够了。
// The code was written by yifan, and yifan is neutral!!!
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define bug puts("NOIP rp ++!");
#define rep(i, a, b, c) for (int i = (a); i <= (b); i += (c))
#define per(i, a, b, c) for (int i = (a); i >= (b); i -= (c))
template<typename T>
inline T read() {
T x = 0;
bool fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? ~x + 1 : x;
}
using pil = pair<ll, int>;
const int N = 2e5 + 5;
int n, q, k, cnt;
int h[N], dep[N], son[N], siz[N];
int tp[N], fa[N];
ll w[N], sum[N];
struct edge {
int v, nxt;
} e[N << 1];
void add(int u, int v) {
e[++ cnt].v = v;
e[cnt].nxt = h[u];
h[u] = cnt;
}
void dfs(int u, int fat) {
dep[u] = dep[fat] + 1;
fa[u] = fat;
siz[u] = 1;
w[u] += w[fat];
for (int i = h[u]; i; i = e[i].nxt) {
int v = e[i].v;
if (v == fat) continue;
dfs(v, u);
siz[u] += siz[v];
if (siz[v] > siz[son[u]]) son[u] = v;
}
}
void getpos(int u, int t) {
tp[u] = t;
if (!son[u]) return ;
getpos(son[u], t);
for (int i = h[u]; i; i = e[i].nxt) {
int v = e[i].v;
if (v == fa[u] || v == son[u]) continue;
getpos(v, v);
}
}
int lca(int x, int y) {
while (tp[x] != tp[y]) {
if (dep[tp[x]] < dep[tp[y]]) swap(x, y);
x = fa[tp[x]];
}
return dep[x] < dep[y] ? x : y;
}
int main() {
n = read<int>(), q = read<int>(), k = read<int>();
rep (i, 1, n, 1) {
w[i] = read<int>();
}
int a, b;
rep (i, 1, n - 1, 1) {
a = read<int>(), b = read<int>();
add(a, b);
add(b, a);
}
dfs(1, 0);
getpos(1, 1);
if (k == 1) {
int x, y, LCA;
rep (i, 1, q, 1) {
x = read<int>(), y = read<int>(), LCA = lca(x, y);
cout << w[x] + w[y] - w[LCA] - w[fa[LCA]];
putchar('\n');
}
}
return 0;
}
