「学习笔记」AC 自动机

AC 自动机是 以 Trie 的结构为基础，结合 KMP 的思想 建立的自动机，用于解决多模式匹配等任务。

Trie 的构建#

这里需要仔细解释一下 Trie 的结点的含义，Trie 中的结点表示的是某个模式串的前缀。我们在后文也将其称作状态。一个结点表示一个状态，Trie 的边就是状态的转移。

形式化地说，对于若干个模式串 $s_1, s_2 \dots s_n$ ，将它们构建一棵字典树后的所有状态的集合记作 Q。

失配指针#

个人感觉这里是最难理解的。

AC 自动机利用一个 fail 指针来辅助多模式串的匹配。

状态 $u$ 的 fail 指针指向另一个状态 $v$ ，其中 $v \in Q$ ，且 $v$ 是 $u$ 的最长后缀（即在若干个后缀状态中取最长的一个作为 fail 指针）。

只需要知道，AC 自动机的失配指针指向当前状态的最长后缀状态即可。

构建指针#

构建 fail 指针，可以参考 KMP 中构造 Next 指针的思想。

考虑字典树中当前的结点 $u$ ， $u$ 的父结点是 $p$ ， $p$ 通过字符 $c$ 的边指向 $u$ ，即 $trie[p,\mathtt{c}]=u$ 。假设深度小于 $u$ 的所有结点的 fail 指针都已求得。

如果 $\text{trie}[\text{fail}[p],\mathtt{c}]$ 存在：则让 $u$ 的 fail 指针指向 $\text{trie}[\text{fail}[p],\mathtt{c}]$ 。相当于在 $p$ 和 $\text{fail}[p]$ 后面加一个字符 $c$ ，分别对应 $u$ 和 fail[u]。
如果 $\text{trie}[\text{fail}[p],\mathtt{c}]$ 不存在：那么我们继续找到 $\text{trie}[\text{fail}[\text{fail}[p]],\mathtt{c}]$ 。重复 $1$ 的判断过程，一直跳 fail 指针直到根结点。
如果真的没有，就让 fail 指针指向根结点。
如此即完成了 $\text{fail}[u]$ 的构建。

如此即完成了 $\text{fail}[u]$ 的构建。

实现#

定义#

struct node {
    int fail;
    int tr[26];
    int End;
} ac[N];

fail 是失配指针，tr 是字典树，End 是当前状态是否为一个字符串的结束。

插入#

这里就是最基本的字典树插入操作。

void Insert(char* s) {
    int l = strlen(s), u = 0;
    for (int i = 0; i < l; ++ i) {
        if (ac[u].tr[s[i] - 'a'] == 0) {
            ac[u].tr[s[i] - 'a'] = ++ tot;
        }
        u = ac[u].tr[s[i] - 'a'];
    }
    ++ ac[u].End;
}

构建失败指针#

我们用队列广搜的方式来构建失败指针，按照上面的步骤：

如果 $\text{trie}[\text{fail}[p],\mathtt{c}]$ 存在：则让 $u$ 的 fail 指针指向 $\text{trie}[\text{fail}[p],\mathtt{c}]$ 。相当于在 $p$ 和 $\text{fail}[p]$ 后面加一个字符 $c$ ，分别对应 $u$ 和 fail[u]。
如果 $\text{trie}[\text{fail}[p],\mathtt{c}]$ 不存在：那么我们继续找到 $\text{trie}[\text{fail}[\text{fail}[p]],\mathtt{c}]$ 。重复 $1$ 的判断过程，一直跳 fail 指针直到根结点。
如果真的没有，就让 fail 指针指向根结点。
如此即完成了 $\text{fail}[u]$ 的构建。

void get_fail() {
	queue<int> q;
	for (int i = 0; i < 26; ++ i) {
		if (ac[0].tr[i] != 0) {
			ac[ac[0].tr[i]].fail = 0;
			q.emplace(ac[0].tr[i]);
		}
	}
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		for (int i = 0; i < 26; ++ i) {
			if (ac[u].tr[i]) {
				ac[ac[u].tr[i]].fail = ac[ac[u].fail].tr[i];
				q.emplace(ac[u].tr[i]);
			} else {
				ac[u].tr[i] = ac[ac[u].fail].tr[i];
			}
		}
	}
}

查询#

这里我们用模板题来说明。

查询有多少个模式串出现过

P3808 【模板】AC 自动机（简单版） - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

int ask(char* s) {
	int l = strlen(s);
	int u = 0, ans = 0;
	for (int i = 0; i < l; ++ i) {
		u = ac[u].tr[s[i] - 'a'];
		for (int cur = u; cur && (~ac[cur].End); cur = ac[cur].fail) {
			ans += ac[cur].End;
			ac[cur].End = -1;
		}
	}
	return ans;
}

这里给 End 打上标记，是为了防止重复搜到这一个模式串，然后重复加入了答案。

完整代码：

/*
  The code was written by yifan, and yifan is neutral!!!
 */

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

template<typename T>
inline T read() {
	T x = 0;
	bool fg = 0;
	char ch = getchar();
	while (ch < '0' || ch > '9') {
		fg |= (ch == '-');
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = (x << 3) + (x << 1) + (ch ^ 48);
		ch = getchar();
	}
	return fg ? ~x + 1 : x;
}

const int N = 1e6 + 5;

int n, tot;
char s[N];

struct node {
	int fail;
	int tr[26];
	int End;
} ac[N];

void Insert(char* s) {
	int l = strlen(s), u = 0;
	for (int i = 0; i < l; ++ i) {
		if (ac[u].tr[s[i] - 'a'] == 0) {
			ac[u].tr[s[i] - 'a'] = ++ tot;
		}
		u = ac[u].tr[s[i] - 'a'];
	}
	++ ac[u].End;
}

void get_fail() {
	queue<int> q;
	for (int i = 0; i < 26; ++ i) {
		if (ac[0].tr[i] != 0) {
			ac[ac[0].tr[i]].fail = 0;
			q.emplace(ac[0].tr[i]);
		}
	}
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		for (int i = 0; i < 26; ++ i) {
			if (ac[u].tr[i]) {
				ac[ac[u].tr[i]].fail = ac[ac[u].fail].tr[i];
				q.emplace(ac[u].tr[i]);
			} else {
				ac[u].tr[i] = ac[ac[u].fail].tr[i];
			}
		}
	}
}

int ask(char* s) {
	int l = strlen(s);
	int u = 0, ans = 0;
	for (int i = 0; i < l; ++ i) {
		u = ac[u].tr[s[i] - 'a'];
		for (int cur = u; cur && (~ac[cur].End); cur = ac[cur].fail) {
			ans += ac[cur].End;
			ac[cur].End = -1;
		}
	}
	return ans;
}

int main() {
	n = read<int>();
	for (int i = 1; i <= n; ++ i) {
		scanf("%s", s + 1);
		Insert(s + 1);
	}
	ac[0].fail = 0;
	get_fail();
	scanf("%s", s + 1);
	cout << ask(s + 1) << '\n';
	return 0;
}

查询出现次数最多的模式串

P3796 【模板】AC 自动机（加强版） - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

这里 End 存储的不再是简单的 $1$ 了，而是当前这个状态对应的模式串的编号，目的是最后输出字符串。

void Insert(string s, int num) {
	int u = 0, l = s.size();
	for (int i = 0; i < l; ++ i) {
		if (!ac[u].tr[s[i] - 'a']) {
			ac[u].tr[s[i] - 'a'] = ++ cnt;
			clr(cnt);
		}
		u = ac[u].tr[s[i] - 'a'];
	}
	ac[u].End = num;
}

for (int i = 1; i <= n; ++ i) {
	cin >> st[i];
	Insert(st[i], i);
	Ans[i].first = 0;
	Ans[i].second = i;
}

除了查询和主函数，其他代码都是一样的。

查询代码：

void ask(char* s) {
	int l = strlen(s);
	int u = 0;
	for (int i = 0; i < l; ++ i) {
		u = ac[u].tr[s[i] - 'a'];
		for (int cur = u; cur; cur = ac[cur].fail) {
			++ Ans[ac[cur].End].first;
		}
	}
}

这里的 Ans 是定义的答案数组，first 是记录出现的次数，second 是该状态的编号。

完整代码：

/*
  The code was written by yifan, and yifan is neutral!!!
 */

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;

template<typename T>
inline T read() {
	T x = 0;
	bool fg = 0;
	char ch = getchar();
	while (ch < '0' || ch > '9') {
		fg |= (ch == '-');
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = (x << 3) + (x << 1) + (ch ^ 48);
		ch = getchar();
	}
	return fg ? ~x + 1 : x;
}

const int N = 1e6 + 5;

int n, cnt;
char s[N];
string st[200];

struct node {
	int fail, End;
	int tr[26];
} ac[N];

pair<int, int> Ans[N];

void clr(int u) {
	for (int i = 0; i < 26; ++ i) {
		ac[u].tr[i] = 0;
	}
	ac[u].fail = ac[u].End = 0;
}

void Insert(string s, int num) {
	int u = 0, l = s.size();
	for (int i = 0; i < l; ++ i) {
		if (!ac[u].tr[s[i] - 'a']) {
			ac[u].tr[s[i] - 'a'] = ++ cnt;
			clr(cnt);
		}
		u = ac[u].tr[s[i] - 'a'];
	}
	ac[u].End = num;
}

void get_fail() {
	queue<int> q;
	for (int i = 0; i < 26; ++ i) {
		if (ac[0].tr[i] != 0) {
			ac[ac[0].tr[i]].fail = 0;
			q.emplace(ac[0].tr[i]);
		}
	}
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		for (int i = 0; i < 26; ++ i) {
			if (ac[u].tr[i]) {
				ac[ac[u].tr[i]].fail = ac[ac[u].fail].tr[i];
				q.emplace(ac[u].tr[i]);
			} else {
				ac[u].tr[i] = ac[ac[u].fail].tr[i];
			}
		}
	}
}

void ask(char* s) {
	int l = strlen(s);
	int u = 0;
	for (int i = 0; i < l; ++ i) {
		u = ac[u].tr[s[i] - 'a'];
		for (int cur = u; cur; cur = ac[cur].fail) {
			++ Ans[ac[cur].End].first;
		}
	}
}

void work() {
	cnt = 0;
	clr(0);
	for (int i = 1; i <= n; ++ i) {
		cin >> st[i];
		Insert(st[i], i);
		Ans[i].first = 0;
		Ans[i].second = i;
	}
	get_fail();
	scanf("%s", s + 1);
	ask(s + 1);
	sort(Ans + 1, Ans + n + 1, [](pii x, pii y) {
		return x.first == y.first ? x.second < y.second : x.first > y.first;
	});
	int l = 1;
	printf("%d\n", Ans[1].first);
	while (Ans[l].first == Ans[1].first) {
		cout << st[Ans[l].second] << '\n';
		++ l;
	}
}

int main() {
	n = read<int>();
	while (n) {
		work();
		n = read<int>();
	}
	return 0;
}

优化#

先拿这道题来引入。P5357 【模板】AC 自动机（二次加强版） - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

你会发现它与 P3796 【模板】AC 自动机（加强版） - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 十分的相似，似乎只要将最后的找出现次数最大的模式串改为输出所有模式串的出现次数就行了 ~~反正当时我是这样想的~~，然后略微修改代码后交上发现。

果然，二次加强版就是不一样……

重新读题，意外发现最后一句话：数据不保证任意两个模式串不相同。

？？？不保证，读错题了！（不要犯这样的低级错误），这里还是比较简单的，只需要判一下重就好了，直接上代码，相信看到这里的聪明的你一定可以看懂它！修改的主要位置加上注释了。

/*
  The code was written by yifan, and yifan is neutral!!!
 */

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

template<typename T>
inline T read() {
	T x = 0;
	bool fg = 0;
	char ch = getchar();
	while (ch < '0' || ch > '9') {
		fg |= (ch == '-');
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = (x << 3) + (x << 1) + (ch ^ 48);
		ch = getchar();
	}
	return fg ? ~x + 1 : x;
}

const int N = 2e5 + 5;
const int M = 2e6 + 5;

int n, tot;
int ans[N], mp[N];
string st[N];
char s[M];
queue<int> q;

struct node {
	int End, fail;
	int tr[26];
} ac[N];

void Insert(string s, int num) {
	int l = s.length(), u = 0;
	for (int i = 0; i < l; ++ i) {
		if (!ac[u].tr[s[i] - 'a']) {
			ac[u].tr[s[i] - 'a'] = ++ tot;
		}
		u = ac[u].tr[s[i] - 'a'];
	}
	if (!ac[u].End) {// 修改点 1
		ac[u].End = num;
	}
	mp[num] = ac[u].End;
}

void get_fail() {
	for (int i = 0; i < 26; ++ i) {
		if (ac[0].tr[i]) {
			ac[ac[0].tr[i]].fail = 0;
			q.emplace(ac[0].tr[i]);
		}
	}
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		for (int i = 0; i < 26; ++ i) {
			if (ac[u].tr[i]) {
				ac[ac[u].tr[i]].fail = ac[ac[u].fail].tr[i];
				q.emplace(ac[u].tr[i]);
			} else {
				ac[u].tr[i] = ac[ac[u].fail].tr[i];
			}
		}
	}
}

void ask(char* s) {
	int l = strlen(s), u = 0;
	for (int i = 0; i < l; ++ i) {
		u = ac[u].tr[s[i] - 'a'];
		for (int cur = u; cur; cur = ac[cur].fail) {
			++ ans[ac[cur].End];
		}
	}
}

int main() {
	n = read<int>();
	for (int i = 1; i <= n; ++ i) {
		cin >> st[i];
		Insert(st[i], i);
	}
	get_fail();
	scanf("%s", s + 1);
	ask(s + 1);
	for (int i = 1; i <= n; ++ i) {
		printf("%d\n", ans[mp[i]]); // 修改点 2
	}
	return 0;
}

再次提交，得到了这样的结果。

没办法，去 $\texttt{OI-Wiki}$ 上看了看，发现原来有优化，优化的方式使用 拓扑排序！

不会拓扑排序的朋友先去学习一下拓扑排序吧。拓扑排序 - OI Wiki (oi-wiki.org)

我们为什么会 T 呢？

看这段代码

void ask(char* s) {
	int l = strlen(s), u = 0;
	for (int i = 0; i < l; ++ i) {
		u = ac[u].tr[s[i] - 'a'];
		for (int cur = u; cur; cur = ac[cur].fail) {
			++ ans[ac[cur].End];
		}
	}
}

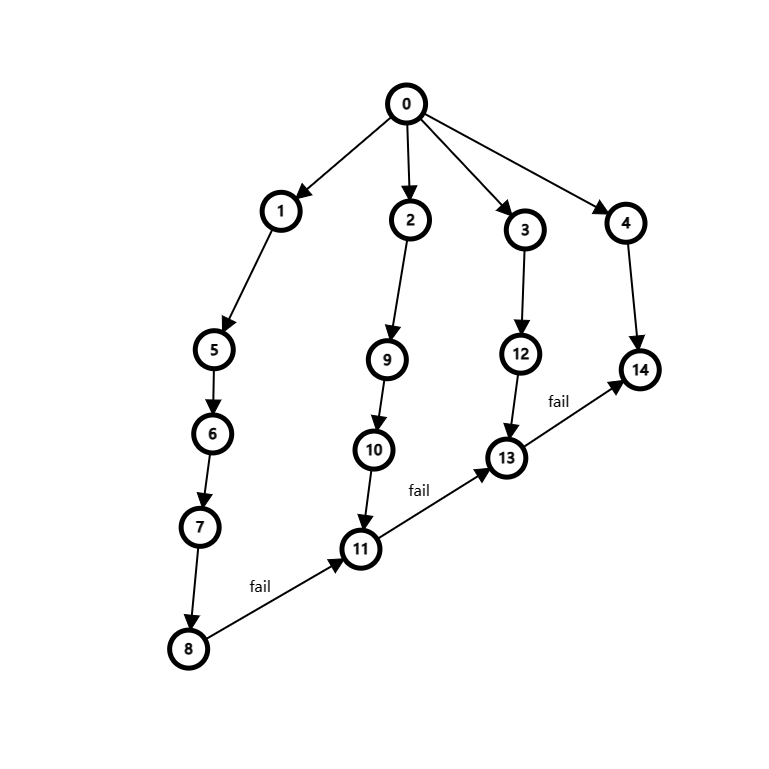
我们沿着 fail 指针一步一步地跳，对于下面的图。

我们假设：

先搜到 $14$ 号节点，答案更新；然后搜到了 $13$ 号节点，答案更新，再找到 $14$ 号节点，答案更新；之后搜到了 $11$ 号节点，顺着 fail 答案更新；再之后搜到了 $8$ 号节点，顺着 fail 答案更新。

你会发现，效率慢的很！然后就被这道题卡了。

如何提高效率的，我们可以在 $8、11、13、14$ 号节点上各打上标记，然后从 $8$ 号开始，标记顺着 fail 传递过去，最后统计的答案为： $8$ 号统计了 $1$ 次， $11$ 号统计了 $2$ 次， $13$ 号统计了 $3$ 次， $14$ 号统计了 $4$ 次，这样统计的答案与一次又一次地更新是一样的，但是这种方法效率高了很多。

具体怎么实现呢，就用拓扑排序，把 fail 指针作为边，最后 fail 指针一定不会成环，所以可以跑拓扑排序，修改一下代码就可以了。

/*
  The code was written by yifan, and yifan is neutral!!!
 */

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

template<typename T>
inline T read() {
	T x = 0;
	bool fg = 0;
	char ch = getchar();
	while (ch < '0' || ch > '9') {
		fg |= (ch == '-');
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = (x << 3) + (x << 1) + (ch ^ 48);
		ch = getchar();
	}
	return fg ? ~x + 1 : x;
}

const int N = 2e5 + 5;
const int M = 2e6 + 5;

int n, tot;
int ans[N], mp[N], in[N];
string st[N];
char s[M];
queue<int> q;

struct node {
	int End, fail, tag;
	int tr[26];
} ac[N];

void Insert(string s, int num) {
	int l = s.length(), u = 0;
	for (int i = 0; i < l; ++ i) {
		if (!ac[u].tr[s[i] - 'a']) {
			ac[u].tr[s[i] - 'a'] = ++ tot;
		}
		u = ac[u].tr[s[i] - 'a'];
	}
	if (!ac[u].End) {
		ac[u].End = num;
	}
	mp[num] = ac[u].End;
}

void get_fail() {
	for (int i = 0; i < 26; ++ i) {
		if (ac[0].tr[i]) {
			ac[ac[0].tr[i]].fail = 0;
			q.emplace(ac[0].tr[i]);
		}
	}
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		for (int i = 0; i < 26; ++ i) {
			if (ac[u].tr[i]) {
				ac[ac[u].tr[i]].fail = ac[ac[u].fail].tr[i];
				q.emplace(ac[u].tr[i]);
				++ in[ac[ac[u].fail].tr[i]];
			} else {
				ac[u].tr[i] = ac[ac[u].fail].tr[i];
			}
		}
	}
}

void ask(char* s) {
	int l = strlen(s), u = 0;
	for (int i = 0; i < l; ++ i) {
		u = ac[u].tr[s[i] - 'a'];
		++ ac[u].tag; // 修改部分 1
	}
}

void topsort() { // 修改部分 2
	for (int i = 1; i <= tot; ++ i) {
		if (!in[i]) {
			q.emplace(i);
		}
	}
	while (!q.empty()) {
		int fr = q.front();
		q.pop();
		ans[ac[fr].End] = ac[fr].tag;
		int u = ac[fr].fail;
		ac[u].tag += ac[fr].tag;
		if (! (-- in[u])) {
			q.emplace(u);
		}
	}
}

int main() {
	n = read<int>();
	for (int i = 1; i <= n; ++ i) {
		cin >> st[i];
		Insert(st[i], i);
	}
	get_fail();
	scanf("%s", s + 1);
	ask(s + 1);
	topsort();
	for (int i = 1; i <= n; ++ i) {
		printf("%d\n", ans[mp[i]]);
	}
	return 0;
}

然后，我们就得到了想要的 AC！

完结！

作者：yifan0305

出处：https://www.cnblogs.com/yifan0305/p/17572382.html

版权：本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议进行许可。

转载时还请标明出处哟！

posted @ 2023-07-21 21:03 yi_fan0305 阅读(202) 评论(1) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 「刷题记录」[JSOI2007] 文本生成器

· 「解题报告」2023-10-17 模拟赛

· AC自动机

· AC 自动机学习笔记

· AC自动机

阅读排行：
· 地球OL攻略 —— 某应届生求职总结
· 周边上新：园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源！
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】

公告

昵称： yi_fan0305
园龄： 2年10个月
粉丝： 30
关注： 50

+加关注

2025年3月

日

一

二

三

四

五

六

Loading

朝气蓬勃后生可畏

四叶草少年，你将何去何从？

「学习笔记」AC 自动机

Trie 的构建#

失配指针#

构建指针#

实现#

定义#

插入#

构建失败指针#

查询#

查询有多少个模式串出现过

查询出现次数最多的模式串

优化#

公告

搜索

常用链接

积分与排名

随笔分类 (193)

随笔档案 (185)

相册 (26)

阅读排行榜

推荐排行榜

最新评论

Loading

朝气蓬勃 后生可畏

四叶草少年，你将何去何从？

「学习笔记」AC 自动机

Trie 的构建#

失配指针#

构建指针#

实现#

定义#

插入#

构建失败指针#

查询#

查询有多少个模式串出现过

查询出现次数最多的模式串

优化#

公告

搜索

常用链接

积分与排名

随笔分类 (193)

随笔档案 (185)

相册 (26)

阅读排行榜

推荐排行榜

最新评论

朝气蓬勃后生可畏