「学习笔记」证明球的体积

为啥写这个呢？
起因是今天下午生物的补课，下课后 zzx 问了我这个问题，一开始没答上来，后来自己认真推了推，然后推出来了，再然后就想写一下过程，以防自己忘了。

---

在数学课本上，我们知道，\(V_{球} = \dfrac{4}{3} \pi R^3\)，而接下来，我们则来证明这个公式的正确性。

证明

如图

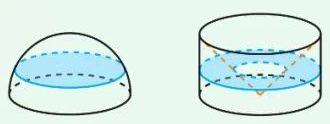
这是两个底面积和高都相等的集合体，左边是半圆，右边是圆柱体从中间挖去了一个圆锥，这个圆锥与圆柱体同底等高。
在此之前，我们要知道一个原理——祖暅原理。

祖暅原理：界于两个平行平面之间的两个立体，被任一平行于这两个平面的平面所截，如果两个截面的面积相等，则这两个立体的体积相等。

我们将它们变成平面图形，如下图：

我们设 \(KL\) 这条平行线为截面，\(AI = KI = JI = R (球体半径相等)，KL = r，LI = PE = x，OP = l\)。
有题目可知，\(MP = NE = R\)，
由图像可知 \(r^2 = R^2 - x^2, \dfrac{l}{R} = \dfrac{x}{R}\)，
所以 \(l = x\)，进而得出 \(r^2 = R^2 - l^2\)
接下来我们来算截面的面积
\(S_1 = \pi r^2, S_2 = \pi (R^2 - l^2) = \pi r^2\)，
因此，\(S_1 = S_2\)，
由祖暅原理可知，这两个集合体的体积相等，即 \(V_{半球} = \pi R^3 - \dfrac{1}{3} \times \pi R^3 = \dfrac{2}{3} \pi R^3\)。
所以，球体的体积为 \(V_{球} = 2\times V_{半球} = 2 \times \dfrac{2}{3} \pi R^3 = \dfrac{4}{3} \pi R^3\)。