Loading

「学习笔记」可持久化线段树

可持久化数据结构 (Persistent data structure) 总是可以保留每一个历史版本，并且支持操作的不可变特性 (immutable)。
主席树全称是可持久化权值线段树，给定 \(n\) 个整数构成的序列 \(a\)，将对于指定的闭区间 \(\left[l, r\right]\) 查询其区间内的第 \(k\) 小值。

图片来自 \(\texttt{OI-wiki}\)

可持久化线段树

变量

#define mid ((l + r) >> 1)
int rot;
int rt[M];

struct node {
	int l, r, val;
} nod[M];

l, r: 左右孩子的指针；
val: 权值；
rot: 动态开点计数器；
rt: 不同版本的根节点的编号。

过程

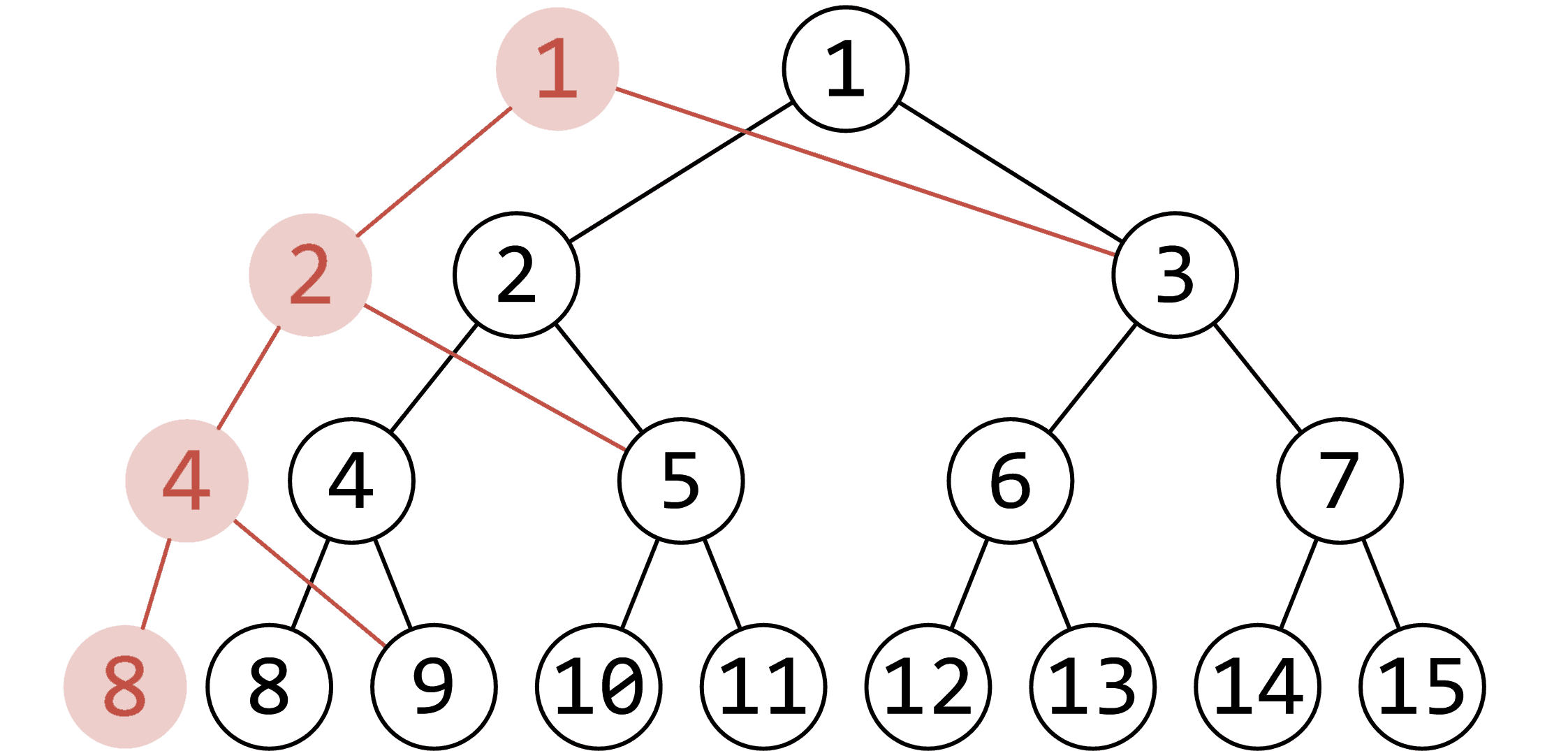
image
每次修改操作修改的点的个数是一样的。
（例如上图，修改了 \(\left[1,8\right]\) 中对应权值为 \(1\) 的结点，红色的点即为更改的点）
只更改了 \(O_{\log{n}}\) 个结点，形成一条链，也就是说每次更改的结点数 \(=\) 树的高度。
主席树不能使用 \(x\times 2，x\times 2+1\) 来表示左右儿子，而是应该动态开点，并保存每个节点的左右儿子编号。
在记录左右儿子的基础上，保存插入每个数的时候的根节点就可以实现持久化。
现在还有个问题，如何求 \(\left[l,r\right]\) 区间 \(k\) 小值。
这里我们再联系另外一个知识：前缀和。
这个小东西巧妙运用了区间减法的性质，通过预处理从而达到 \(O_1\) 回答每个询问。
我们可以发现，主席树统计的信息也满足这个性质。
如果需要得到 \(\left[l,r\right]\) 的统计信息，只需要用 \(\left[1,r\right]\) 的信息减去 \(\left[1,l - 1\right]\) 的信息就行了。
关于空间问题，直接上个 \(2^5\times 10^5\)（即 n << 5，大多数题目中空间限制都较为宽松，因此一般不用担心空间超限的问题）。

操作

  • 建树

int build(int l, int r) {
	int u = ++ rot;
	if (l == r) {
		return u;
	}
	nod[u].l = build(l, mid);
	nod[u].r = build(mid + 1, r);
	return u;
}

  • 创建新节点

inline int newnod(int u) {
	++ rot;
	nod[rot] = nod[u];
	nod[rot].val = nod[u].val + 1;
	return rot;
}

修改时是在原来版本的基础上进行修改，先设置它们一样，由于插入了一个新的数，所以 nod[rot].val = nod[u].val + 1;。

  • 插入新节点

int add(int u, int l, int r, int pos) {
	u = newnod(u);
	if (l == r)	return u;
	if (pos <= mid) {
		nod[u].l = add(nod[u].l, l, mid, pos);
	}
	else {
		nod[u].r = add(nod[u].r, mid + 1, r, pos);
	}
	return u;
}

if (pos <= mid) {
	nod[u].l = add(nod[u].l, l, mid, pos);
}
else {
	nod[u].r = add(nod[u].r, mid + 1, r, pos);
}

修改时只会修改一条链，那也就意味着只会修改左孩子或右孩子中的一个，另一个保持不变。

  • 查询第 \(k\) 大

int query(int l, int r, int lr, int rr, int k) {
	int x = nod[nod[rr].l].val - nod[nod[lr].l].val;
	if (l == r)	return l;
	if (k <= x) {
		return query(l, mid, nod[lr].l, nod[rr].l, k);
	}
	else {
		return query(mid + 1, r, nod[lr].r, nod[rr].r, k - x);
	}
}

int x = nod[nod[rr].l].val - nod[nod[lr].l].val;

这里利用了前缀和，求的是在 \(lr\) 到 \(rr\) 这个版本之间，左孩子的数量增加了多少，即 \(\left[lr, rr\right]\) 的前 \(x\) 小的元素。

if (k <= x) {
	return query(l, mid, nod[lr].l, nod[rr].l, k);
}
else {
	return query(mid + 1, r, nod[lr].r, nod[rr].r, k - x);
}

如果 \(k < x\)，那么说明第 \(k\) 大的数在右孩子上，否则就在左子树上。

可持久化数组

这个来源于洛谷的【模板】可持久化线段树 1（可持久化数组），需要支持修改操作，但没有了查询第 \(k\) 大操作和插入操作。

变量

#define mid ((l + r) >> 1)
int rot;
int rt[M];

struct node {
	int ls, rs, val;
} nod[(N << 5) + 10];

操作

  • 创建新节点

inline int newnod(int u) { // 创建新节点
	++ rot;
	nod[rot] = nod[u];
	return rot;
}

  • 建树

int build(int l, int r) { // 建树
	int u = ++ rot;
	if (l == r) {
		scanf("%d", &nod[u].val);
		return u;
	}
	nod[u].ls = build(l, mid);
	nod[u].rs = build(mid + 1, r);
	return u;
}

  • 修改

int modify(int u, int l, int r, int pos, int c) { // 修改
	u = newnod(u);
	if (l == r) {
		nod[u].val = c;
	}
	else {
		if (pos <= mid) {
			nod[u].ls = modify(nod[u].ls, l, mid, pos, c);
		}
		else {
			nod[u].rs = modify(nod[u].rs, mid + 1, r, pos, c);
		}
	}
	return u;
}

  • 查询

int query(int u, int l, int r, int pos) { // 查询
	if (l == r) {
		return nod[u].val;
	}
	else {
		if (pos <= mid) {
			return query(nod[u].ls, l, mid, pos);
		}
		else {
			return query(nod[u].rs, mid + 1, r, pos);
		}
	}
}

模板

namespace Persistent { // 可持久化数据结构
#define mid ((l + r) >> 1)
	
	const int N = 1e6 + 5;
	const int M = (N << 5) + 10;
	
	struct persistent_arr { // 可持久化数组
		int rot;
		int rt[M];
		
		struct node {
			int ls, rs, val;
		} nod[(N << 5) + 10];
		
		inline int newnod(int u) { // 创建新节点
			++ rot;
			nod[rot] = nod[u];
			return rot;
		}
		
		int build(int l, int r) { // 建树
			int u = ++ rot;
			if (l == r) {
				scanf("%d", &nod[u].val);
				return u;
			}
			nod[u].ls = build(l, mid);
			nod[u].rs = build(mid + 1, r);
			return u;
		}
		
		int modify(int u, int l, int r, int pos, int c) { // 修改
			u = newnod(u);
			if (l == r) {
				nod[u].val = c;
			}
			else {
				if (pos <= mid) {
					nod[u].ls = modify(nod[u].ls, l, mid, pos, c);
				}
				else {
					nod[u].rs = modify(nod[u].rs, mid + 1, r, pos, c);
				}
			}
			return u;
		}
		
		int query(int u, int l, int r, int pos) { // 查询
			if (l == r) {
				return nod[u].val;
			}
			else {
				if (pos <= mid) {
					return query(nod[u].ls, l, mid, pos);
				}
				else {
					return query(nod[u].rs, mid + 1, r, pos);
				}
			}
		}
	};
	
	struct persistent_seg {
		int rot;
		int rt[M];
		
		struct node {
			int l, r, val;
		} nod[M];
		
		inline int newnod(int u) { // 创建新节点
			++ rot;
			nod[rot] = nod[u];
			nod[rot].val = nod[u].val + 1;
			return rot;
		}
		
		int build(int l, int r) { // 建树
			int u = ++ rot;
			if (l == r) {
				return u;
			}
			nod[u].l = build(l, mid);
			nod[u].r = build(mid + 1, r);
			return u;
		}
		
		int add(int u, int l, int r, int pos) { // 插入新节点
			u = newnod(u);
			if (l == r)	return u;
			if (pos <= mid) {
				nod[u].l = add(nod[u].l, l, mid, pos);
			}
			else {
				nod[u].r = add(nod[u].r, mid + 1, r, pos);
			}
			return u;
		}
		
		int query(int l, int r, int lr, int rr, int k) { // 查找第 k 大的值
			int x = nod[nod[rr].l].val - nod[nod[lr].l].val;
			if (l == r)	return l;
			if (k <= x) {
				return query(l, mid, nod[lr].l, nod[rr].l, k);
			}
			else {
				return query(mid + 1, r, nod[lr].r, nod[rr].r, k - x);
			}
		}
	};
}

例题

【模板】可持久化线段树 1（可持久化数组）

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define mid ((l + r) >> 1)

const int N = 1e6 + 5;

int n, m, rot;
int a[N], rt[N];

inline int read() {
	int x = 0;
	int fg = 0;
	char ch = getchar();
	while (ch < '0' || ch > '9') {
		fg |= (ch == '-');
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = (x << 3) + (x << 1) + (ch ^ 48);
		ch = getchar();
	}
	return fg ? ~x + 1 : x;
}

struct node {
	int ls, rs, val;
} nod[(N << 5) + 10];

inline int newnod(int u) {
	++ rot;
	nod[rot] = nod[u];
	return rot;
}

int build(int l, int r) {
	int u = ++ rot;
	if (l == r) {
		nod[u].val = a[l];
		return u;
	}
	nod[u].ls = build(l, mid);
	nod[u].rs = build(mid + 1, r);
	return u;
}

int modify(int u, int l, int r, int pos, int c) {
	u = newnod(u);
	if (l == r) {
		nod[u].val = c;
	}
	else {
		if (pos <= mid) {
			nod[u].ls = modify(nod[u].ls, l, mid, pos, c);
		}
		else {
			nod[u].rs = modify(nod[u].rs, mid + 1, r, pos, c);
		}
	}
	return u;
}

int query(int u, int l, int r, int pos) {
	if (l == r) {
		return nod[u].val;
	}
	else {
		if (pos <= mid) {
			return query(nod[u].ls, l, mid, pos);
		}
		else {
			return query(nod[u].rs, mid + 1, r, pos);
		}
	}
}

int main() {
	n = read(), m = read();
	for (int i = 1; i <= n; ++ i) {
		a[i] = read();
	}
	rt[0] = build(1, n);
	for (int i = 1, x, op, pos, val; i <= m; ++ i) {
		x = read(), op = read(), pos = read();
		if (op == 1) {
			val = read();
			rt[i] = modify(rt[x], 1, n, pos, val);
		}
		else {
			printf("%d\n", query(rt[x], 1, n, pos));
			rt[i] = rt[x];
		}
	}
}

【模板】可持久化线段树 2

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define mid ((l + r) >> 1)

const int N = 1e6 + 5;
const int M = (N << 5) + 10;

int n, m;
int rot;
int a[N], tmp[N], rt[N];

struct node {
	int l, r, val;
} nod[M];

inline int getid(int c, int len) {
	return lower_bound(tmp + 1, tmp + len + 1, c) - tmp;
}

inline int newnod(int u) {
	++ rot;
	nod[rot] = nod[u];
	nod[rot].val = nod[u].val + 1;
	return rot;
}

int build(int l, int r) {
	int u = ++ rot;
	if (l == r) {
		return u;
	}
	nod[u].l = build(l, mid);
	nod[u].r = build(mid + 1, r);
	return u;
}

int add(int u, int l, int r, int pos) {
	u = newnod(u);
	if (l == r)	return u;
	if (pos <= mid) {
		nod[u].l = add(nod[u].l, l, mid, pos);
	}
	else {
		nod[u].r = add(nod[u].r, mid + 1, r, pos);
	}
	return u;
}

int query(int l, int r, int lr, int rr, int k) {
	int x = nod[nod[rr].l].val - nod[nod[lr].l].val;
	if (l == r)	return l;
	if (k <= x) {
		return query(l, mid, nod[lr].l, nod[rr].l, k);
	}
	else {
		return query(mid + 1, r, nod[lr].r, nod[rr].r, k - x);
	}
}

int main() {
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; ++ i) {
		scanf("%d", a + i);
		tmp[i] = a[i];
	}
	sort(tmp + 1, tmp + n + 1);
	int len = unique(tmp + 1, tmp + n + 1) - tmp - 1;
	rt[0] = build(1, len);
	for (int i = 1; i <= n; ++ i) {
		rt[i] = add(rt[i - 1], 1, len, getid(a[i], len));
	}
	for (int i = 1, l, r, k; i <= m; ++ i) {
		scanf("%d%d%d", &l, &r, &k);
		printf("%d\n", tmp[query(1, len, rt[l - 1], rt[r], k)]);
	}
	return 0;
}
posted @ 2023-05-04 20:44  yi_fan0305  阅读(261)  评论(1)  编辑  收藏  举报