「学习笔记」博弈论——公平组合游戏入门
定义
公平组合游戏 \(\text{(Impartial Game)}\) 的定义如下：
游戏有两个人参与，二者轮流做出决策，双方均知道游戏的完整信息；
任意一个游戏者在某一确定状态可以作出的决策集合只与当前的状态有关，而与游戏者无关；
游戏中的同一个状态不可能多次抵达，游戏以玩家无法行动为结束，且游戏一定会在有限步后以非平局结束。
状态与博弈图
我们将每个点视为一个状态，再由每个节点向它的后继节点连边，这样就形成了一个有向无环图，例如下图。
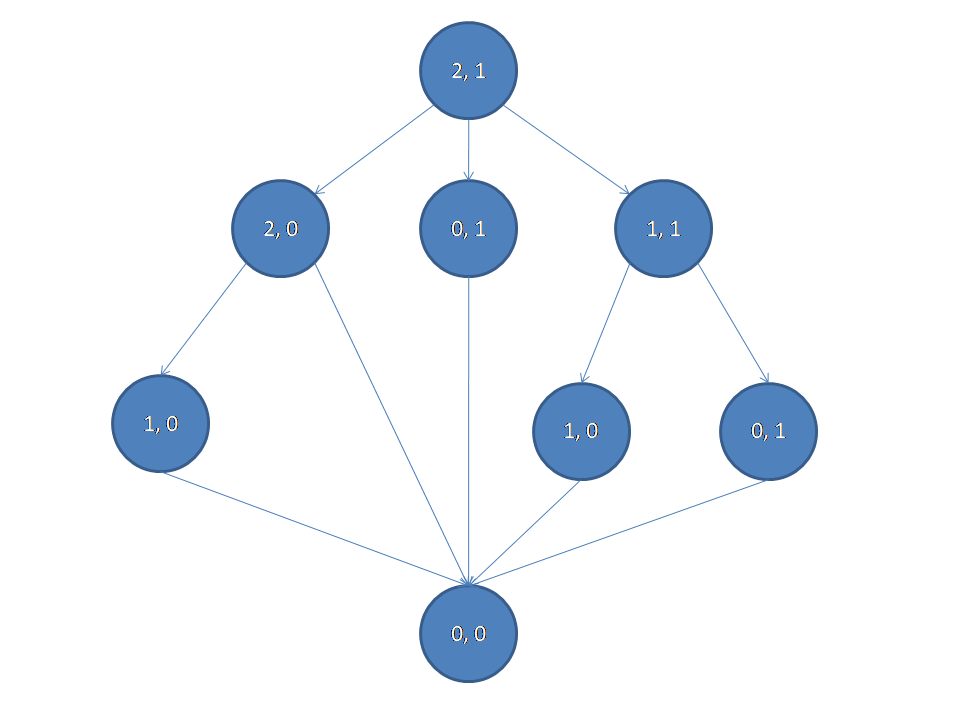
定义：必胜状态为先手必胜的状态，必败状态为先手必败的状态。
定理：
- 没有后继状态的为必败状态。
无法继续操作，所以必败。 - 一个必胜状态存在至少一个必败状态为它的后继状态。
先手操作后，会到达一个必败状态，此时后手为必败状态，对应的先手为必胜状态。 - 一个必败状态的所有后继状态都为必胜状态。
无论先手如何操作，都能到达一个必胜状态，此时后手为必胜状态，对应的先手为必败状态。
巴什博弈
问题描述
有两个人玩取石子的游戏，这堆石子一共有 \(n\) 个，两人轮流进行，每次可以取 \(1 \sim m\) 个石子，先取光石子的一方胜利，游戏中两人都采用 最优策略。
博弈分析
- 当 \(n \le m\) 时，先手必胜。
- 当 \(n = m + 1\) 时，无论怎么取，先手必败。
- 当 \(n = m + 1 + m\) 时，先手可以先取走 \(m\) 个，留下 \(m + 1\) 个给后手，这样先手必胜。
我们可以发现，面临着剩余石子数为 \(m + 1\) 的一方一定必败，因此，双方的最优策略是通过拿石子来使对方面临的剩余石子数为 \(m + 1\) 个。
推广一下：
- \(n = k \times (m + 1) + r\) 时，先手拿 \(r\) 个，后手拿 \(x\) 个 \((1 \le x \le m)\)，先手再拿 \(m + 1 - x\) 个，这样下去，一定是后手面临 \(m + 1\) 的必败局面，因此先手必胜。
- \(n = k \times (m + 1)\) 时，先手拿 \(x\) 个 \((1 \le x \le m)\)，后手拿 \(m + 1 - x\) 个，这样下去，一定是先手面临 \(m + 1\) 的必败局面，因此先手必败。
代码：
#include <cstdio>
using namespace std;
typedef long long ll;
int T, n, m;
void work() {
scanf("%d%d", &n, &m);
if (n % (m + 1)) {
puts("first");
}
else {
puts("second");
}
}
int main() {
scanf("%d", &T);
while (T --) {
work();
}
return 0;
}
\(\text{nim}\) 游戏
问题描述
有两个人在玩 \(\text{nim}\) 取石子游戏，地上有 \(n\) 堆石子，每个人可以从任意一堆石子中取出任意个扔掉，可以取完，不能不取，且每次只能从一堆里取，谁先没有石子可取谁就输了，问谁会胜利，两个人都采取 最优策略。
博弈分析
我们可以先随便画出一个博弈图。
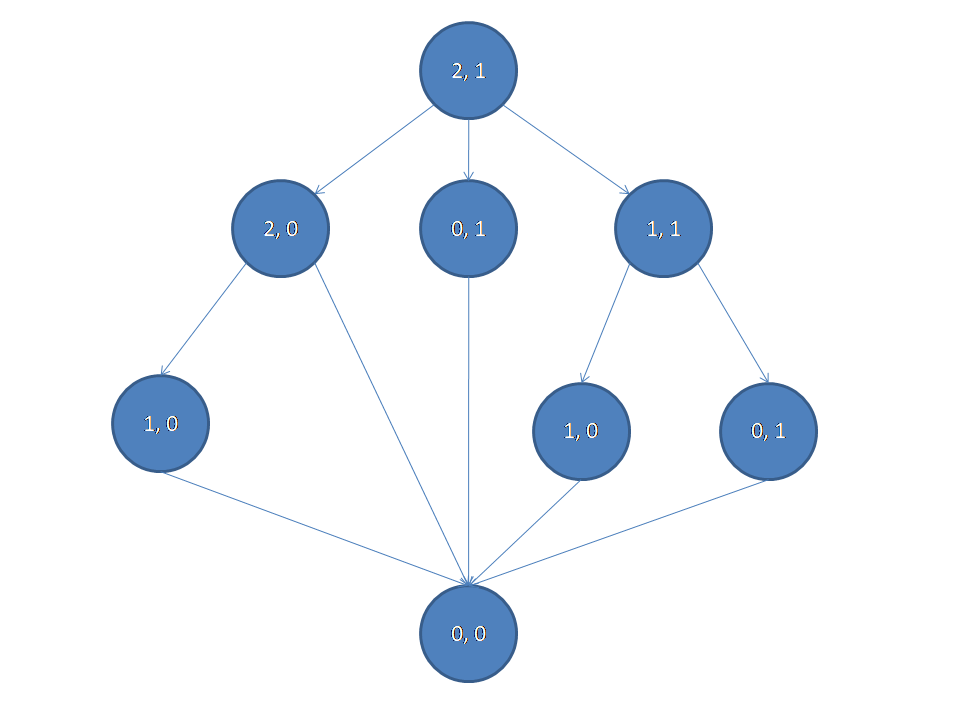
通过绘画博弈图，我们可以用 \(O_{(\prod_{i = 1}^{n}a_i)}\) 的复杂度来求得该局面是否先手先赢。
但是，这个复杂度会 \(\text{T}\) 飞的，有没有什么办法来代替这个恐怖的复杂度？
其实前辈们给我们留了一个办法——\(\text{Nim}\) 和。
定义 \(\text{Nim}\) 和为 \(a_1 \oplus a_2 \oplus \ldots \oplus a_n\)。
当 \(a_1 \oplus a_2 \oplus a_3 \cdots = 0\) 时，先手必败。
证明：
根据博弈图，只需证明以下定理：
- 没有后继状态的为必败状态。
- 对于 \(a_1 \oplus a_2 \oplus \ldots \oplus a_n \neq 0\) 的局面，一定存在某种移动使得 \(a_1 \oplus a_2 \oplus \ldots \oplus a_n = 0\)。
- 对于 \(a_1 \oplus a_2 \oplus \ldots \oplus a_n = 0\) 的局面，一定不存在某种移动使得 \(a_1 \oplus a_2 \oplus \ldots \oplus a_n = 0\)。
没有后继状态，即全 \(0\) 局面，\(a_1 \oplus a_2 \oplus \ldots \oplus a_n = 0\)。
假设 \(a_1 \oplus a_2 \oplus \ldots \oplus a_n = k\)，则我们只需将 \(a_i\) 改为 \(a_i \oplus k\)，就能使这个式子成立。
假设 k 的二进制最高位 \(1\) 为 \(d\)，即 \(2^d \le k < 2^{d + 1}\)。根据异或定义，一定有奇数个 \(a_i\) 的二进制第 \(d\) 位为 \(1\)。满足这个条件的 \(a_i\) 一定也满足 \(a_i > a_i \oplus k\)，因而这也是个合法的移动。
如果我们要将 \(a_i\) 改为 \(a_i'\)，则根据异或运算律可以得出 \(a_i = a_i'\)，因而这不是个合法的移动。
#include <cstdio>
using namespace std;
typedef long long ll;
const int N = 1e4 + 5;
int T, n, m;
ll ans, a;
void work() {
ans = 0;
scanf("%d", &n);
for (int i = 1; i <= n; ++ i) {
scanf("%lld", &a);
ans ^= a;
}
if (!ans) {
puts("No");
}
else {
puts("Yes");
}
}
int main() {
scanf("%d", &T);
while (T --) {
work();
}
return 0;
}
