「刷题记录」POJ 1149 PIGS 猪

题目传送门：POJ 1149
网络流的好题
建图：因为有 \(n\) 个顾客，所以一共会进行 \(n\) 次交易，在每次交易中，没上锁的猪舍之间的猪可以相互转移，而我们为了让下一个顾客买到尽可能多的猪，可以把猪集中到下一个顾客与当前顾客都可以打开的猪舍里，建立一个超级汇点，连接所有的顾客，流量为顾客的需量，而在可以互相交换猪的的猪舍之间，也连边，流量为正无穷，顾客与其对应的猪舍之间也连边，流量为猪舍中猪的数量，建立一个超级源点，流量也为猪舍中猪的数量，大概图示如下

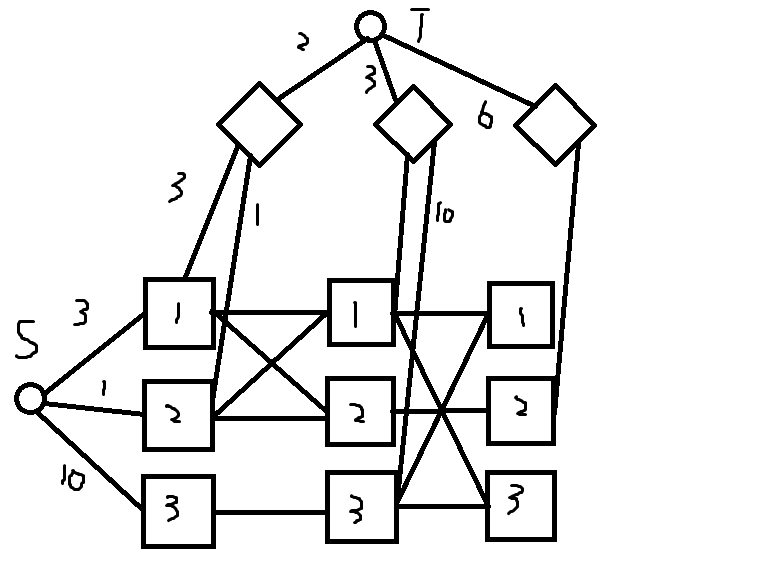
这里，我们发现，有些路径源点相同，到达的顾客也相同，我们可以将这些边进行合并，同时我们发现，对于第一次打开 \(i\) 号猪舍的顾客，在他之前 \(i\) 号猪舍的猪没有进行转移，所以这些猪舍连向该顾客的边的流量就是该猪舍的数量，我们可以将图进行压缩，如下

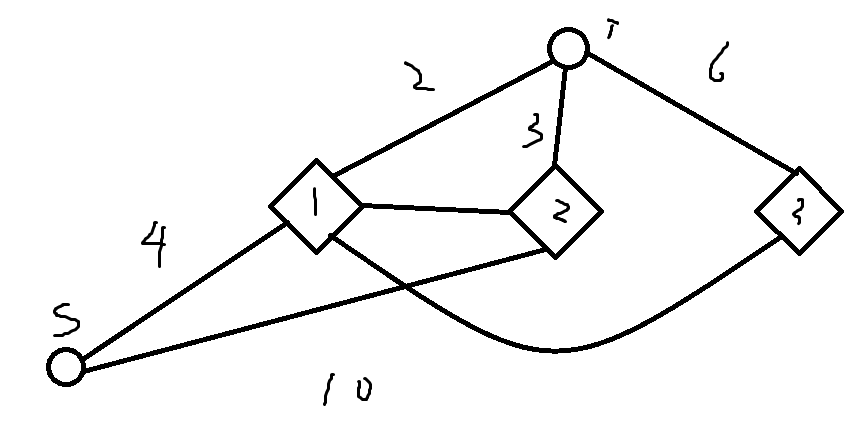
简洁多了
我们根据这个建图，跑最大流算法就行了
上代码：

#include <iostream>
#include <cstdio>
#include <queue>
using namespace std;
typedef long long ll;

inline ll read() {
	ll x = 0;
	int fg = 0;
	char ch = getchar();
	while (ch < '0' || ch > '9') {
		fg |= (ch == '-');
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = (x << 3) + (x << 1) + (ch ^ 48);
		ch = getchar();
	}
	return fg ? ~x + 1 : x;
}

const int N = 110;
const int M = 1100;
const int E = 1e6 + 5;
const ll inf = 1e18;

int n, m, S, T, cnt;
ll maxflow;
int h[N], cur[N], pre[M], dep[N], inque[N];
ll a[M];
queue<int> q;

struct edge {
	int v, nxt;
	ll w;
} e[E];

void add(int u, int v, ll w) {
	e[++ cnt].v = v;
	e[cnt].w = w;
	e[cnt].nxt = h[u];
	h[u] = cnt;
}

int bfs() {
	for (int i = 0; i <= T; ++ i) {
		dep[i] = 1e9;
		inque[i] = 0;
		cur[i] = h[i];
	}
	while (!q.empty()) {
		q.pop();
	}
	q.push(S);
	inque[S] = 1, dep[S] = 0;
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		inque[u] = 0;
		for (int i = h[u]; i; i = e[i].nxt) {
			int v = e[i].v;
			if (dep[v] > dep[u] + 1 && e[i].w) {
				dep[v] = dep[u] + 1;
				if (!inque[v]) {
					q.push(v);
					inque[v] = 1;
				}
				if (v == T)	return 1;
			}
		}
	}
	return 0;
}

ll dfs(int u, ll flow) {
	if (u == T) {
		maxflow += flow;
		return flow;
	}
	ll used = 0, rlow = 0;
	for (int i = cur[u]; i; i = e[i].nxt) {
		cur[u] = i;
		int v = e[i].v;
		if (e[i].w && dep[v] == dep[u] + 1) {
			rlow = dfs(v, min(flow - used, e[i].w));
			if (rlow) {
				e[i].w -= rlow;
				e[i ^ 1].w += rlow;
				used += rlow;
				if (used == flow)	break;
			}
		}
	}
	return used;
}

int main() {
	m = read(), n = read();
	for (int i = 1; i <= m; ++ i) {
		a[i] = read();
	}
	T = n + 1;
	cnt = 1;
	for (int i = 1; i <= n; ++ i) {
		int k = read(), u;
		ll y = 0;
		for (int j = 1; j <= k; ++ j) {
			int x = read();
			if (pre[x] == 0) {
				y += a[x];
			}
			else {
				add(pre[x], i, inf);
				add(i, pre[x], 0);
			}
			pre[x] = i;
		}
		add(S, i, y);
		add(i, S, 0);
		u = read();
		add(i, T, u);
		add(T, i, 0);
	}
	while (bfs()) {
		dfs(S, inf);
	}
	printf("%lld\n", maxflow);
	return 0;
}