「学习笔记」Dinic算法
网络瘤
时间复杂度:\(O_{n^2m}\),在稀疏图上和 EK 算法相当,在稠密图上的效率比 EK 算法更高
Dinic 算法步骤
- bfs 分层
- dfs 找增广路
- 重复以上两个步骤
bfs 分层
从源点出发,给每一个点设置一个层数,像这样
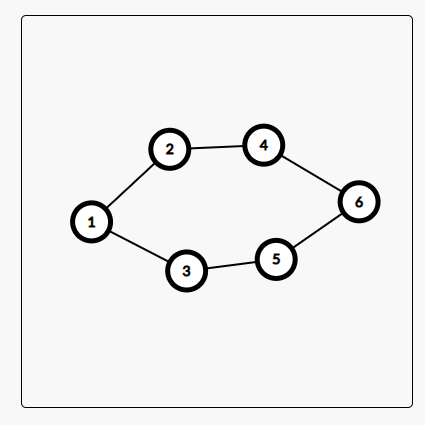
\(1\) 号节点是第 \(1\) 层,\(2\)、\(3\) 号节点是第 \(2\) 层,\(4\)、\(5\) 号节点是第 \(3\) 层,\(6\) 号节点是第 \(4\) 层。
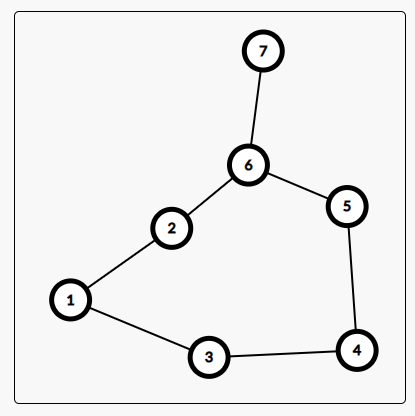
在这个图中,选一个最短路径,你不会选 \(1 \rightarrow 3 \rightarrow 4 \rightarrow 5 \rightarrow 6 \rightarrow 7\) 这个路径
这里还要注意,我们分层是根据点的深度和是否还有流量来分的,如果最后分层时汇点已经不在分层中了,那就退出即可
整完分层,我们就可以找增广路了
先上代码:
int bfs() {
memset(dep, 127, sizeof dep); // dep 分层的深度
memset(inque, 0, sizeof inque); // inque 是否在队列内
while (!q.empty()) {
q.pop();
}
q.push(s);
dep[s] = 0;
while (!q.empty()) {
int u = q.front();
q.pop();
inque[u] = 0; // 标志出队
for (int i = h[u]; i; i = e[i].nxt) {
int v = e[i].v;
if (dep[v] > dep[u] + 1 && e[i].w) { // 这条边还有流量
dep[v] = dep[u] + 1;
if (!inque[v]) {
q.push(v); // 入队,从这个点再更新其他的点
inque[v] = 1; // 标志入队
}
if (v == t) return true; // 可以到达汇点
}
}
}
return false;
}
dfs 找增广路
dfs 向下搜索,只能往下一层的节点搜,不能返回或跳层,一直搜到汇点,返回最后到达汇点的流量,每条路径的流量再减去最后返回的流量
上代码:
ll dfs(int u, ll flow) {
if (u == t) return flow; // 到达汇点
ll rlow = 0;
for (int i = h[u]; i; i = e[i].nxt) {
int v = e[i].v;
if (e[i].w && dep[v] == dep[u] + 1) { // 只流入下一层,还要有流量
if ((rlow = dfs(v, min(flow, e[i].w)))) {
e[i].w -= rlow; // 减去流过去的流量
e[i ^ 1].w += rlow; // 反向边,以便于反悔
return rlow;
}
}
}
return 0;
}
初始版本的 Dinic
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read() {
ll x = 0;
int fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? ~x + 1 : x;
}
const int N = 210;
const int M = 5010;
const ll inf = 1e18;
int n, m, s, t, cnt;
int h[N], dep[N], inque[N];
queue<int> q;
struct edge {
int v, nxt;
ll w;
} e[M << 1];
void add(int u, int v, ll w) {
e[++ cnt].v = v;
e[cnt].nxt = h[u];
h[u] = cnt;
e[cnt].w = w;
}
int bfs() {
memset(dep, 127, sizeof dep); // dep 分层的深度
memset(inque, 0, sizeof inque); // inque 是否在队列内
while (!q.empty()) {
q.pop();
}
q.push(s);
dep[s] = 0;
while (!q.empty()) {
int u = q.front();
q.pop();
inque[u] = 0;
for (int i = h[u]; i; i = e[i].nxt) {
int v = e[i].v;
if (dep[v] > dep[u] + 1 && e[i].w) { // 这条边还有流量
dep[v] = dep[u] + 1;
if (!inque[v]) {
q.push(v);
inque[v] = 1;
}
if (v == t) return true; // 可以到达汇点
}
}
}
return false;
}
ll dfs(int u, ll flow) {
if (u == t) return flow; // 到达汇点
ll rlow = 0;
for (int i = h[u]; i; i = e[i].nxt) {
int v = e[i].v;
if (e[i].w && dep[v] == dep[u] + 1) { // 只流入下一层
if ((rlow = dfs(v, min(flow, e[i].w)))) {
e[i].w -= rlow; // 减去流过去的流量
e[i ^ 1].w += rlow; // 反向边反悔
return rlow;
}
}
}
return 0;
}
int main() {
n = read(), m = read(), s = read(), t = read();
cnt = 1;
for (int i = 1; i <= m; ++ i) {
int u = read(), v = read();
ll w = read();
add(u, v, w);
add(v, u, 0);
}
ll lowflow, ans = 0;
while (bfs()) {
while ((lowflow = dfs(s, inf))) {
ans += lowflow;
}
}
printf("%lld\n", ans);
return 0;
}
当然,如果说上面是初始版本,那就说明这个东西是有优化的
小优化
上面的代码中,我们每次 dfs,搜到汇点就直接返回,而再一次开始搜则是从原点重新开始搜,这样的话效率就很低下,跑得慢,那我们为什么不继续搜下去找到最后用了多少流量,然后一次返回呢?
先上代码:
ll dfs(int u, ll flow) {
if (u == t) {
vis = 1;
maxflow += flow;
return flow; // 到达汇点
}
ll rlow = 0, used = 0;
for (int i = h[u]; i; i = e[i].nxt) {
int v = e[i].v;
if (e[i].w && dep[v] == dep[u] + 1) { // 只流入下一层
if ((rlow = dfs(v, min(flow - used, e[i].w)))) {
used += rlow;
e[i].w -= rlow; // 减去流过去的流量
e[i ^ 1].w += rlow; // 反向边反悔
if (used == flow) break;
}
}
}
return used;
}
while (bfs()) {
vis = 1;
while (vis == 1) {
vis = 0;
dfs(s, inf);
}
}
这段 dfs 代码中,used 表示已经流过多少流量了,flow 表示流入这条路径的流量是多少,所以我们用剩余的流量来继续往下搜,知道没有增广路或流量用完了为止
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read() {
ll x = 0;
int fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? ~x + 1 : x;
}
const int N = 210;
const int M = 5010;
const ll inf = 1e18;
int n, m, s, t, cnt, vis;
ll maxflow;
int h[N], dep[N], inque[N], cur[N];
queue<int> q;
struct edge {
int v, nxt;
ll w;
} e[M << 1];
void add(int u, int v, ll w) {
e[++ cnt].v = v;
e[cnt].nxt = h[u];
h[u] = cnt;
e[cnt].w = w;
}
int bfs() {
memset(dep, 127, sizeof dep); // dep 分层的深度
memset(inque, 0, sizeof inque); // inque 是否在队列内
while (!q.empty()) {
q.pop();
}
q.push(s);
dep[s] = 0;
while (!q.empty()) {
int u = q.front();
q.pop();
inque[u] = 0;
for (int i = h[u]; i; i = e[i].nxt) {
int v = e[i].v;
if (dep[v] > dep[u] + 1 && e[i].w) { // 这条边还有流量
dep[v] = dep[u] + 1;
if (!inque[v]) {
q.push(v);
inque[v] = 1;
}
if (v == t) return true; // 可以到达汇点
}
}
}
return false;
}
ll dfs(int u, ll flow) {
if (u == t) {
vis = 1;
maxflow += flow;
return flow; // 到达汇点
}
ll rlow = 0, used = 0;
for (int i = h[u]; i; i = e[i].nxt) {
int v = e[i].v;
if (e[i].w && dep[v] == dep[u] + 1) { // 只流入下一层
if ((rlow = dfs(v, min(flow - used, e[i].w)))) {
used += rlow;
e[i].w -= rlow; // 减去流过去的流量
e[i ^ 1].w += rlow; // 反向边反悔
if (used == flow) break;
}
}
}
return used;
}
int main() {
n = read(), m = read(), s = read(), t = read();
cnt = 1;
for (int i = 1; i <= m; ++ i) {
int u = read(), v = read();
ll w = read();
add(u, v, w);
add(v, u, 0);
}
while (bfs()) {
vis = 1;
while (vis == 1) {
vis = 0;
dfs(s, inf);
}
}
printf("%lld\n", maxflow);
return 0;
}
传说中的当前弧优化
当前弧优化,可以把弧看作边,就是从当前的路径继续往下搜,什么意思呢?我们 h 数组中存的,是从这个点出发的最后一条边,但是我们 dfs 时,从最后一条边开始,每一条边都进行了增广,而且增广得很彻底,所以从最后一条边到当前我们所在的边中间所有的边对我们而言,都已经是“废边”了,那就直接从当前边开始继续往下搜,设置一个 cur 数组来存储当前边,这个 cur 会随着循环的进行而改变,具体看代码
int bfs() {
for (int i = 1; i <= n; ++ i) {
dep[i] = 1e9; // dep 分层的深度
inque[i] = 0; // inque 是否在队列内
cur[i] = h[i]; // 当前弧优化
}
while (!q.empty()) {
q.pop();
}
q.push(s);
dep[s] = 0;
while (!q.empty()) {
int u = q.front();
q.pop();
inque[u] = 0;
for (int i = h[u]; i; i = e[i].nxt) {
int v = e[i].v;
if (dep[v] > dep[u] + 1 && e[i].w) { // 这条边还有流量
dep[v] = dep[u] + 1;
if (!inque[v]) {
q.push(v);
inque[v] = 1;
}
if (v == t) return true; // 可以到达汇点
}
}
}
return false;
}
ll dfs(int u, ll flow) {
if (u == t) {
maxflow += flow;
return flow; // 到达汇点
}
ll rlow = 0, used = 0;
for (int &i = cur[u]; i; i = e[i].nxt) { // 当前弧优化
int v = e[i].v;
if (e[i].w && dep[v] == dep[u] + 1) { // 只流入下一层
if ((rlow = dfs(v, min(flow - used, e[i].w)))) {
used += rlow;
e[i].w -= rlow; // 减去流过去的流量
e[i ^ 1].w += rlow; // 反向边反悔
if (used == flow) break;
}
}
}
return used;
}
下面就是最终版的 Dinic 算法!
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read() {
ll x = 0;
int fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? ~x + 1 : x;
}
const int N = 210;
const int M = 5010;
const ll inf = 1e18;
int n, m, s, t, cnt;
ll maxflow;
int h[N], dep[N], inque[N], cur[N];
queue<int> q;
struct edge {
int v, nxt;
ll w;
} e[M << 1];
void add(int u, int v, ll w) {
e[++ cnt].v = v;
e[cnt].nxt = h[u];
h[u] = cnt;
e[cnt].w = w;
}
int bfs() {
for (int i = 1; i <= n; ++ i) {
dep[i] = 1e9; // dep 分层的深度
inque[i] = 0; // inque 是否在队列内
cur[i] = h[i]; // 当前弧优化
}
while (!q.empty()) {
q.pop();
}
q.push(s);
dep[s] = 0;
while (!q.empty()) {
int u = q.front();
q.pop();
inque[u] = 0;
for (int i = h[u]; i; i = e[i].nxt) {
int v = e[i].v;
if (dep[v] > dep[u] + 1 && e[i].w) { // 这条边还有流量
dep[v] = dep[u] + 1;
if (!inque[v]) {
q.push(v);
inque[v] = 1;
}
if (v == t) return true; // 可以到达汇点
}
}
}
return false;
}
ll dfs(int u, ll flow) {
if (u == t) {
maxflow += flow;
return flow; // 到达汇点
}
ll rlow = 0, used = 0;
for (int &i = cur[u]; i; i = e[i].nxt) { // 当前弧优化
int v = e[i].v;
if (e[i].w && dep[v] == dep[u] + 1) { // 只流入下一层
if ((rlow = dfs(v, min(flow - used, e[i].w)))) {
used += rlow;
e[i].w -= rlow; // 减去流过去的流量
e[i ^ 1].w += rlow; // 反向边反悔
if (used == flow) break;
}
}
}
return used;
}
int main() {
n = read(), m = read(), s = read(), t = read();
cnt = 1;
for (int i = 1; i <= m; ++ i) {
int u = read(), v = read();
ll w = read();
add(u, v, w);
add(v, u, 0);
}
while (bfs()) {
dfs(s, inf);
}
printf("%lld\n", maxflow);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号