「学习笔记」线段树
介绍:
线段树是一棵二叉搜索树，思想与分治很想，把一段区间平分平分再平分，平分到不能平分为止，可以进行方便的区间修改和区间查询，当然，树状数组能做的单点修改、单点查询，线段树也可以更好地实现，总之，线段树是树状数组的升级版，此外，线段树能做的平衡树也能做，但平衡树码量太大，考场上一般写不出来反正我是写不出来，就是会写也不会用，其次有些特殊的线段树如权值线段树也可以水过平衡树，可见，线段树的应用还是十分广泛的。
图片来自 \(\texttt{OI-Wiki}\)
建树：
一般的线段树都是递归建树，当然，也有一种不用递归建树的线段树，即非递归线段树——zkw 线段树
当然，zkw 线段树并不是我们现在的主角，我们讲一下递归建树的操作
首先，可以设置三个方便的宏定义偷懒
typedef long long ll;
#define ls (p << 1)
#define rs (p << 1 | 1)
#define mid ((l + r) >> 1)
// ls 左儿子 rs 右儿子 mid 中间值
因为线段树是棵二叉树，\(p\) 是当前节点的编号，所以一个结点的左儿子和右儿子可以表示为\(p \times 2\) 和 \(p \times 2 + 1\)，用位运算速度更快，但是要注意运算符之间的优先级，不熟悉的那就勤加括号吧反正加几个括号基本没影响，还不容易出错，不加白不加，至于这个 \(mid\)，纯粹是图省事
刚才我们也讲了左右儿子的表示方法，所以我们的空间要开到原来的四倍，当然，线段树还有一种结构体存法，那个存法开两倍空间即可，但要维护的东西不少，所以也没剩多少空间，而且操作起来很麻烦，不如用这种左右儿子表示法来存储
ll val[N << 2];
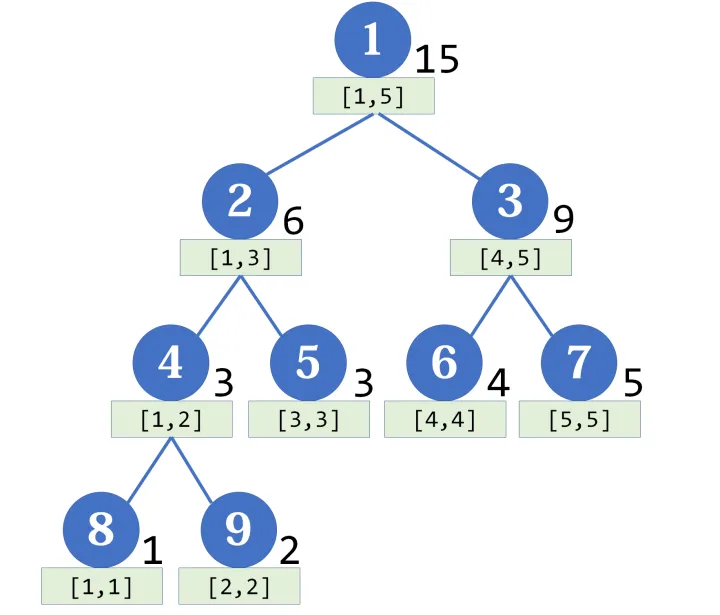
如图，这是一颗线段树，每一个节点都代表着一个区间的信息，如 \(1\) 号节点代表着区间 \([1, 5]\)的和，\(4\) 代表着区间 \([1, 2]\) 的和，我们发现它是从中间值平分开的，这里就是分治的思想，二分，每部分在自己递归，最后再合并一下，上代码
void build(int p, int l, int r) {
if (l == r) {
val[p] = read();
return ;
}
build(ls, l, mid);
build(rs, mid + 1, r);
pushup(p);
}
代码也不是很长，宏定义是个好东西
对于 pushup 函数，你可能会想知道这是什么东西，别急，这就是接下来我们要讲的
更新函数
更新函数，说白了就是将两个儿子的信息合并，合并的方式有多种，相加、相乘、取最值、dp 等等，具体题目具体分析，这里就展示一下相加类型的更新函数，要记住，建树和修改操作等一些操作，一定不要忘记更新！！！
void pushup(int p) {
val[p] = val[ls] + val[rs];
}
到这里，建树部分才算正式完成，接下来就是各种操作了
众所周知，线段树对于区间操作那可是十分厉害的，虽然树状数组也能实现区间操作，但是太麻烦，还要背公式，相对于线段树也不好理解，因此对于区间操作，一般都用线段树，还有一个东西叫分块，也是可以的当然并不是主角
区间修改
还是刚刚的图
修改区间 \([1 , 5]\)，在线段树上，\([1 , 5]\) 可以由 \([1, 4], [5, 5]\) 组成，在这里我们可以看出，当一段小区间属于这个修改的大区间时，我们可以直接对这个小区间进行操作，不必继续向下修改，但如果后面又对这个小区间中的更小的区间，如\([3, 3]\)进行修改，然后要查询它的值怎么办呢？这里我们要引入一个新的变量——\(lazy\)，俗称懒标记。
线段树中的每一个元素都需要一个懒标记，所以它也要开到源数据的\(4\)倍
ll lazy[N << 2];
懒标记，由名得知，它很懒，为什么？因为它懒得继续向下一个一个元素修改，但判断这个区间全部属于要修改的大区间时，直接对着对当前节点进行标记，同时 \(lazy\) 负责记录对这个区间的操作，节省时间由此可以看出，懒也有懒的好处，它的含义是对当前节点的区间中所有的元素都进行一个操作，\(lazy\)也有很多类型，有的负责记录区间加减，有的负责记录区间乘除，还有负责乘方开方、是否异或等等，设置 \(lazy\) 的含义在一些题目当中也是一个难点，具体题目具体分析，在区间修改中，\(lazy\) 主要也是为了省时，这里以区间加减的修改函数为例
void change(int p, int l, int r, int lr, int rr, ll v) {
if (lr <= l && r <= rr) {
lazy[p] += v;
val[p] += v * (r - l + 1);
return ;
}
pushdown(p, l, r);
if (lr <= mid) {
change(ls, l, mid, lr, rr, v);
}
if (rr > mid) {
change(rs, mid + 1, r, lr, rr, v);
}
pushup(p);
}
// l、r 当前节点所对应的区间 lr、rr 要修改的区间的左右边界 v 区间要加减的数
向下递归过程中，如果现在节点对应的区间 \([l, r]\) 已经被修改区间 \([lr, rr]\)包含，直接对当前节点进行操作，具体操作如代码所示，很好理解，不细说，\(lazy\) 加上 \(v\)，代表这段区间整体加上 \(v\)，如果有不属于\([lr, rr]\)的部分，分治，如果 \(lr\) 小于等于中间值，说明在当前对应区间的左半段有要进行修改操作的，向左孩子递归，\(rr\) 大于中间值，说明在当前对应区间的右半段也又要修改操作的，向右孩子递归，最后，不要忘记更新！，至于 pushdown 操作，这就和我们的 \(lazy\) 有关了，我们存下 \(lazy\)，但是 \(lazy\) 到底在哪里有作用呢，这就引出了我们的
下传函数和区间查询
为了方便，我们一起将！区间查询这个操作，字面意思，就是个查询操作，但怎么查询才能更快呢，先上图
假设，我们要查询区间[1, 5]的所有数的和，那我们只需要查询 \(1\) 号节点的数值就行了，\(1\) 号节点存储着区间 \([1, 5]\) 的和，所以，查询操作与修改操作有着一样的思路，遇到全属于大区间的小区间，直接返回小区间的值就行了
但这里有个问题，假设我们已经对区间 \([1, 2]\) 都加上了 \(v\)，按照我们的修改操作，直接对 \(4\) 号节点进行更新，记录 \(lazy\)，那我现在要查询区间 \([1, 1]\)，即 \(8\) 号节点的信息怎么办，当初的修改操作压根就没递归到这一层，这时候，\(lazy\) 就派上用场了，还记得 \(lazy\) 的含义吗？对区间内所有的元素都进行一个操作，那么，我们是否可以把这个 \(lazy\) 下传给左右儿子呢？反正左右儿子都是属于这个区间的，这个修改也是对它们的修改，所以下传这个 \(lazy\) 没有什么影响，那我们就下传，这里就是加减操作的下传函数的代码。
void pushdown(int p, int l, int r) {
if (!lazy[p]) return ; // 没有lazy还下传个毛线
lazy[ls] += lazy[p], val[ls] += lazy[p] * (mid - l + 1);
lazy[rs] += lazy[p], val[rs] += lazy[p] * (r - mid);
lazy[p] = 0; // 下传完了,它的lazy也就没了
}
查询要下传，为什么修改也要下传呢？当然是因为修改函数中有 pushup 函数，最后一更新，本来已经修改好的正确答案会被更新掉，如果下传了 \(lazy\)，那么更新后还是原来的正确答案，否则，最后会被错误答案代替，现在解决了 \(lazy\) 的问题，我们也就可以开心的进行区间查询了，上代码。
ll query(int p, int l, int r, int lr, int rr) {
if (lr <= l && r <= rr) {
return val[p];
}
pushdown(p, l, r);
ll ans = 0;
if (lr <= mid) ans += query(ls, l, mid, lr, rr);
if (rr > mid) ans += query(rs, mid + 1, r, lr, rr);
return ans;
}
区间操作就讲这么多，具体还是 \(lazy\) 与下传、更新函数的操作，具体题目具体分析
前面说了，树状数组能做的线段树都能做，那么树状数组的单点修改、单点查询在线段树上是 so easy 的，都是递归，没什么技术含量，只需 change 函数的 \(lr, rr\) 都设成要修改的位置，就完成了，query 函数是一样的，当然也可以自己再写个函数，下面给个例子
void update(int p, int l, int r, int x, ll v) {
if (l == r) {
val[p] += v;
return ;
}
if (x <= mid) {
update(ls, l, mid, x, v);
}
else update(rs, mid + 1, r, x, v);
pushup(p);
}
ll query(int p, int l, int r, int x) {
if (l == r) {
return val[p];
}
if (x <= mid) return query(ls, l, mid, x);
else return query(rs, mid + 1, r, x);
}
真的毫无技术含量
其他
\(lazy\) 方面，有一种优化方法叫标记永久化
标记永久化：如果确定懒惰标记不会在中途被加到溢出（即超过了该类型数据所能表示的最大范围），那么就可以将标记永久化。标记永久化可以避免下传懒惰标记，只需在进行询问时把标记的影响加到答案当中，从而降低程序常数。具体如何处理与题目特性相关，需结合题目来写。这也是树套树和可持久化数据结构中会用到的一种技巧。——\(\text{OI wiki}\)
空间方面，有动态开点优化，可以与权值线段树搭配
线段树方面，还有一些其他的线段树，如权值线段树、zkw 线段树。
权值线段树，叶节点代表的不再是区间范围，而是权值，非叶节点代表的是权值区间而不是我们原本的区间，加上动态开点，可以水过洛谷的普通平衡树
zkw线段树，先%为敬，非递归线段树，因为不递归，跑的是真的很快，但是不好理解，其次在竞赛中，初学者是真的不会用这个去做题，所以对像我这样的蒟蒻而言，也就拿它玩玩，水水模板，然后就吃灰了，这里给出洛谷普通线段树 \(1\) 的 zkw 线段树代码
zkw 线段树
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 5;
int n, num = 1, m;
ll tree[N << 2], delta[N << 2];
inline ll read() {
ll x = 0;
int fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? ~x + 1 : x;
}
void print(ll x, char y) {
cout << x;
putchar(y);
}
void build() {
for (; num <= n + 1; num <<= 1);
for (int i = num + 1; i <= num + n; ++ i) {
tree[i] = read();
}
for (int i = num - 1; i >= 1; -- i) {
tree[i] = tree[i << 1] + tree[i << 1 | 1];
}
}
void change(int l, int r, ll v) {
int lNum = 0, rNum = 0, nNum = 1;
for (l = num + l - 1, r = num + r + 1; l ^ r ^ 1; l >>= 1, r >>= 1, nNum <<= 1) {
tree[l] += v * lNum;
tree[r] += v * rNum;
if (~l & 1) {
delta[l ^ 1] += v;
tree[l ^ 1] += v * nNum;
lNum += nNum;
}
if (r & 1) {
delta[r ^ 1] += v;
tree[r ^ 1] += v * nNum;
rNum += nNum;
}
}
for (; l; l >>= 1, r >>= 1) {
tree[l] += v * lNum;
tree[r] += v * rNum;
}
}
ll query(int l, int r) {
int lNum = 0, rNum = 0, nNum = 1;
ll ans = 0;
for (l = num + l - 1, r = num + r + 1; l ^ r ^ 1; l >>= 1, r >>= 1, nNum <<= 1) {
if (delta[l]) {
ans += delta[l] * lNum;
}
if (delta[r]) {
ans += delta[r] * rNum;
}
if (~l & 1) {
ans += tree[l ^ 1];
lNum += nNum;
}
if (r & 1) {
ans += tree[r ^ 1];
rNum += nNum;
}
}
for (; l; l >>= 1, r >>= 1) {
ans += delta[l] * lNum;
ans += delta[r] * rNum;
}
return ans;
}
int main() {
n = read();
m = read();
build();
for (int op, x, y, i = 1; i <= m; ++ i) {
op = read(), x = read(), y = read();
if (op == 1) {
ll v = read();
change(x, y, v);
}
else {
print(query(x, y), '\n');
}
}
return 0;
}
其他方面的这些东西，有些很有用，有些也就图一乐，以后如果学会了，我会来补坑的。
标记永久化：「学习笔记」线段树标记永久化
可持久化线段树（权值线段树）：「学习笔记」可持久化线段树
