「学习笔记」差分约束

浅谈#

差分约束主要是处理这样一类问题
有n个像 $x_1-x_2\le k$ 这样的式子，求 $x_1$ 到 $x_n$ 的最大/最小值

差分约束#

看到这一类题目，如果你认为是数学题，很好，你完蛋了
这一类题目会假扮成数学不等式出现，正解是利用这些信息来建图
我们把上面的式子变化一下
$x_1-x_2 \le k$
$x_1 \le x_2+k$
看到这个式子，你再看这个式子 $dis_1=dis_2+k$，两者有没有相似之处？
一定有，对吧？除了 $<$，这两个式子差不多，我们如果要建图，按照一般思路，边权肯定取这个 $=$，而不是 $<$ 不然你怎么知道边权是多少，这个 $=$ 是我们在这个式子中唯一可以确定边权的符号，因此，对于形似 $x_1-x_2<k$ 这样的式子，我们要把它转化成 $x_1-x_2 \le k-1$ 才能做题。

具体做法#

差分约束的题目，一般就是求最大值或最小值
但一般不是难在转化式子，而是难在找这些限制条件(即上面的不等式)
当你找出限制条件时，我们就根据题目来转化建图
对于最大值，将式子都转化成 $x_1-x_2 \le k$ 的形式，再将式子转化成 $x_1 \le x_2+k$ 的形式，这样就是连接一条 $x_2$ 到 $x_1$ 边权为 $k$ 的边，建好图后，我们跑最短路
首先，这里怎么将 $x_1-x_2 \ge k$ 转化？$\times(-1)$ 就行了，不等式两边同乘一个负数，不等号方向改变
然后，为什么跑最短路？
我们画一个图

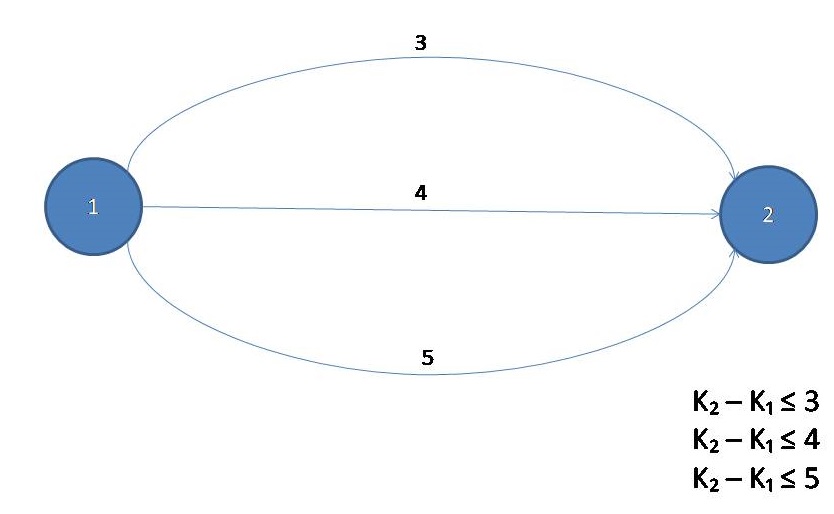
这是一个图，右下角是他的限制条件，限制条件作为不等式，肯定也是要满足不等式性质的，根据不等式性质，同小取小，所以，每条边跑最短路。
同理，对于最小值，将式子转化为 $x_1-x_2 \ge k$ 的形式，连接一条 $x_2$ 到 $x_1$ 边权为 $k$ 的边，建图，跑最长路

实现#

题目中一般会问有没有一种方案可以满足所有的限制条件，建图的时候，可能就会有环(正环-最长路或负环-最短路)，这样就会卡掉 $\text{dijkstra}$,所以我们用 $\text{SPFA}$ 来实现最短路和最长路
关于SPFA，它死了，但没完全死

提醒#

判断环，有 $\text{dfs-SPFA}$ 和 $\text{bfs-SPFA}$ 两种算法，单纯只是判断负环，$\text{dfs-SPFA}$ 对于随机数据效率比 $\text{bfs-SPFA}$ 高了不知道多少，但有些毒瘤出题人会卡掉 $\text{dfs-SPFA}$，$\text{dfs-SPFA}$ 会在负环模板等数据中产生指数级别的复杂度，所以，具体用哪个，自己掂量一下吧 反正dfs-SPFA和bfs-SPFA都能被卡，一半死一半不死呗

例题#

丢下例题准备跑路
小K的农场原先卡bfs-SPFA，现在卡dfs-SPFA
模板题别问我为什么模板题放后面
poj3169啊哈！又是奶牛

结尾#

其实约束分为三种：线性约束、区间约束、未知条件约束，但这是关于找限制条件的事情，就不讲了我是不会告诉你我不会的
最后，喜欢可以支持一下呀
在写这篇文章的时候，教练突然过来了，差点就死了，看在我这么惨的情况下，我能不要脸的要一个支持吗?QWQ

完结撒花！#