「学习笔记」平衡树——splay 二
链接
OK,我们继续上文，来讲一些其他操作。
七、找排名为 \(k\) 的数
和 treap 的操作很像，都是通过比较左右子树和该节点的大小来查找。
ll k_th(int x)
{
int id=root;
if(siz[id]<x) return 0;
while(1)
{
int y=ch[id][0];
if(x>siz[y]+cnt[id])
{
x-=(siz[y]+cnt[id]);
id=ch[id][1];
}
else
{
if(siz[y]>=x) id=y;
else return val[id];
}
}
}
八、清理（一般删除之后用)
void cls(int x)
{
fa[x]=ch[x][0]=ch[x][1]=siz[x]=cnt[x]=val[x]=0;//清理干净,以绝后患
}
这里要注意，这里只是把该节点的信息删除了，不要忘记把父亲的关系也切断，这个是最重要的
九、递归建树
相较于单点一个一个插入，在已知点权的情况下，可以直接递归建一棵树，这样效率更高
但是，要注意你是根据数据的下标建的树还是点权建的树，依据不同，操作也不同
其次，为了方便区间操作，一般留出第一个位置 a[1] 和最后一个位置，增加哨兵
a[1]=-INF;
for(rint i=2;i<=n+1;++i)
a[i]=i-1;
a[n+2]=INF;
root=build(1,n+2,0);
int build(int l,int r,int f)//l 左边界 r 右边界 f 初始化为0
{
if(l>r) return 0;
int mid=l+r>>1;
fa[mid]=f;
ch[mid][0]=build(l,mid-1,mid);
ch[mid][1]=build(mid+1,r,mid);
pushup(mid);
return mid;
}
十、下传懒标记
void pushdown(int id)
{
if(!lazy[id]) return;
//进行操作......
}
在一些操作中，如旋转、 find 、翻转、加减，等等，一定不要忘记 pushdown
例如：旋转的懒标记下传
void spin(int x)
{
rint y=fa[x],z=fa[y],d=(x==ch[y][1]);
pushdown(y),pushdown(x);//懒标记下传
ch[z][ch[z][1]==y]=x,fa[x]=z;
ch[y][d]=ch[x][d^1],fa[ch[x][d^1]]=y;
ch[x][d^1]=y,fa[y]=x;
pushup(y);
pushup(x);
}
十一、找数 \(x\) 的排名
这个其实与前面的 find 一样，只是返回左子树的大小即可
insert(-INF);
insert(INF);
find(x);
printf("%lld\n",siz[ch[root][0]]+(val[root]<x?cnt[root]:0));
void find(ll x)
{
int u=root;
if(!u) return;//不存在该节点,直接返回
while(ch[u][x>val[u]]&&x!=val[u])//找到该节点的位置
u=ch[u][x>val[u]];
splay(u,0);//伸展
}
接下来就是区间操作的主场了
区间操作
区间操作：指定区间\(（l \sim r）\),查找排序为 \(l-1\) 的节点并伸展至根，查找排序为 \(r+1\) 的节点并伸展至 \(root\) 下，则节点 \(r+1\) 的左子树就是所要的区间。为了操作的方便，在不影响的结果的情况下，可以在两端增加哨兵。
如图依旧扒的教练的
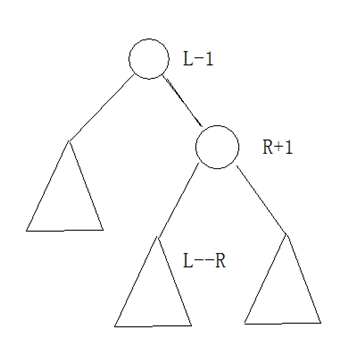
根据二叉查找树的性质，\(R+1\) 的左孩子就是 \(L-R\) 范围的数据
区间操作都是以这个思路为基础的，前面的删点操作也是运用的这个思路，明白这个，后面才可以进行
pushdown 函数随时用上
每次伸展时都要保证懒标记已下传
void check(int now)//保证所有懒标记都下传了
{
int id=root;
int k=root;
while(1)
{
pushdown(k);
if(now==k)break;
if(now>k)k=ch[k][1];
else k=ch[k][0];
}
}
十二、翻转
操作比较简单，交换左右孩子然后下传懒标记即可，但要注意，一棵树被翻转了两次并没有发生变化，所以它的懒标记只有 \(1\) 和 \(0\) 两种，主要注意 pushdown 函数就好了
建树时要根据下标建树
void pushdown(int id)
{
if(!rev[id]) return;
swap(ch[id][0],ch[id][1]);
rev[ch[id][0]]^=1;
rev[ch[id][1]]^=1;
rev[id]=0;
}
void rever(int l,int r)
{
int pre=find(l-1),nxt=find(r+1);
splay(pre,0);
splay(nxt,pre);
int x=ch[nxt][0];
rev[x]^=1;
}
十三、区间加减
和线段树差不多，其实线段树能做的，平衡树也能做到，平衡树能很简单的做到的，线段树就不一定能做到了
在伸展操作之前，一定要保证懒标记都下传了
void pushup(int id)
{
sum[id]=sum[ch[id][0]]+sum[ch[id][1]]+val[id];
siz[id]=siz[ch[id][0]]+siz[ch[id][1]]+1;
}
void add(int id,ll v)
{
if(!id) return;
sum[id]+=siz[id]*v;
laz[id]+=v;
val[id]+=v;
}
void pushdown(int id)
{
if(!laz[id]) return;
add(ch[id][0],laz[id]);
add(ch[id][1],laz[id]);
laz[id]=0;
}
void change(int l,int r,int v)
{
int pre=get(l,0),nxt=get(r,1);
splay(pre,0);splay(nxt,pre);
add(ch[nxt][0],v);
pushup(nxt);
pushup(pre);
}
十四、区间求和
和线段树操作几乎一模一样
void query(int l,int r)
{
int pre=get(l,0),nxt=get(r,1);
splay(pre,0);splay(nxt,pre);
printf("%lld",sum[ch[nxt][0]]);
}
一般用的应该就这些了吧，如果有，我会补充的 QWQ！
总之就是一句话，线段树能做的，平衡树也能做！
