「学习笔记」最小表示法
通过这个算法,我认识到了,取模,是一个神奇的东西!还有,暴力出奇迹!
——$\text{yi_fan0305}$的学后感
进入正题
定义:最小表示法是用于解决字符串最小表示问题的方法。
(当我第一次学习时,我:??????,所以,别慌,看不懂定义是正常现象)
前置知识——循环同构
对于字符串 \(S\),有一个位置 \(i\) ,可以满足
那么我们称 \(S\) 与 \(T\) 循环同构,举个例子,字符串 \(123456789\) 的循环同构有 \(678912345、234567891\) 等等
最小表示
字符串 \(S\) 的最小表示就是与 \(S\) 循环同构的所有字符串中字典序最小的字符串
例如: 字符串 \(987654321\) 的最小表示为 \(198765432\)
最小表示法
最小表示法就是找最小表示问题的算法,你可以发现,这个东西可以打暴力来解决
我们设字符串 \(S\),\(S\) 的循环同构 \(S1\) 是在 \(S\) 中以 \(i\) 为起点,循环同构 \(S2\) 是在 \(S\) 中以 \(j\) 为起点,已经判断的长度为 \(k\),如下图
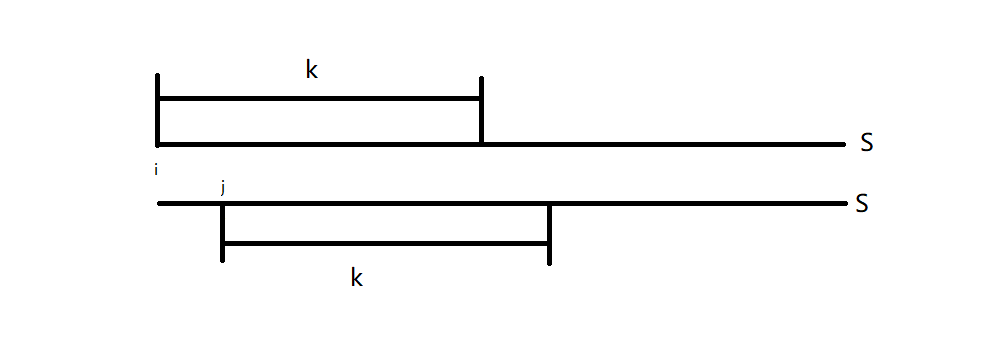
我们一个一个比较,如果两个位置的字符相等,++ k,继续向后搜,如果不相等,比较两个位置的大小,因为我们求的是最小表示,所以我们将大的舍弃,假设 \(S1_{i+ k} > S2_{j + k}\),那么我们就将 \(S1\) 舍弃,++ i,将下一个循环同构与 \(S2\) 进行比较,\(k\) 再变成 \(0\),从头开始比较
代码
int min_show() {
int i = 0, j = 1, k = 0;
while (i < n && j < n && k < n) {
if (a[(i + k) % n] == a[(j + k) % n]) {
++ k;
}
else {
if (a[(i + k) % n] > a[(j + k) % n]) {
++ i;
}
else {
++ j;
}
k = 0;
if (i == j) {
++ i;
}
}
}
return min(i, j);
}
这个暴力在一般情况下是可以应付过去的,但在一些特殊数据中,这个暴力会变成 \(O_{n^2}\) 的,如 \(cccccccccccccccc......cccd\) 这样的,所以,我们要优化一下这个暴力
我们假设循环同构 \(S1、S2\) 的前 \(p\) 个字符是相等的,\(S1\) 的起始点为 \(i\),\(S2\) 的起始点为 \(j\),那么,当 \(S1_{g + 1} > S2_{g + 1}\) 时,按照暴力的操作,我们要将 \(i\) 加 \(1\),但是,对于以 \(i + 1\) 为起点的新的循环同构,一定会有以 \(j + 1\) 为起点的循环同构比它更优,这个性质在扩大一点范围,任意以 \(i + p\) 为起点的循环同构,都一定会有一个以 \(j + p\) 为起点的循环同构比它更优,前提 \(p \in [0, k]\),所以,我们可以将 ++ i 变为 += k + 1,即跳过 \([i, i + k]\) 这一段
优化完后,这个暴力就变成了最小表示法了,看,暴力出奇迹!
代码:
int min_show() {
int i = 0, j = 1, k = 0;
while (i < n && j < n && k < n) {
if (a[(i + k) % n] == a[(j + k) % n]) {
++ k;
}
else {
if (a[(i + k) % n] > a[(j + k) % n]) {
i += (k + 1);
}
else {
j += (k + 1);
}
if (i == j) {
++ i;
}
k = 0;
}
}
return min(i, j);
}
后记
观察这个代码,你会发现一个起始点是 \(0\),所以你要从 \(0\) 开始输入,但由于我不习惯这种写法,所以就想方设法取模,让这个算法从 \(1\) 开始输入也能找到答案,最后,我失败了,只能说,取模是个神奇的东西
这里给出完整代码,所对应的题目是洛谷的模板题,告诉你个卡常小技巧:取模的速度其实很慢,我们可以将取模改成减法,再配合 #define 宏定义,可以提一下速度(快不了很多),下面的代码中有
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define mod(x) (x >= n ? x - n : x)
inline ll read() {
ll x = 0;
int fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? -x : x;
}
const int N = 3e5 + 5;
int n;
ll a[N];
int min_show() {
int i = 0, j = 1, k = 0;
while (i < n && j < n && k < n) {
int x = i + k, y = j + k;
if (a[mod(x)] == a[mod(y)]) {
++ k;
}
else {
if (a[mod(x)] > a[mod(y)]) {
i += k + 1;
}
else {
j += k + 1;
}
if (i == j) {
++ i;
}
k = 0;
}
}
return min(i, j);
}
int main() {
n = read();
for (int i = 0; i < n; ++ i) {
a[i] = read();
}
int ans = min_show();
for (int i = 0; i < n; ++ i) {
int x = i + ans;
printf("%lld ", a[mod(x)]);
}
return 0;
}

