「学习笔记」Manacher算法(马拉车算法)
来自度娘的介绍:Manachar 算法主要是处理字符串中关于回文串的问题的,它可以在 \(O_n\) 的时间处理出以字符串中每一个字符为中心的回文串半径,由于将原字符串处理成两倍长度的新串,在每两个字符之间加入一个特定的特殊字符,因此原本长度为偶数的回文串就成了以中间特殊字符为中心的奇数长度的回文串了。
回文串:正读和反读都一样的字符串
通过这个简介,我们知道了这个算法就是找回文串的,下面说一下具体操作
1、在原字符串中插入符号,将每个字符隔开
举个例子,原字符串为 aabbccbbaa,隔开后就变为了 a#a#b#b#c#c#b#b#a#a,在中间插入 #,是为了更好的确定中点,如果一个回文串是奇数串,那中点很好确定,就在字符上,但如果一个回文串是偶数串,那中点就是中间两个字符的空隙,如果不插入 #,就很难表示,当然,插入的符号随意,不一定非要是 #。
为了防止越界,也为了能让程序停止,我们可以在起点和终点各设一个不同的符号,就像这样 $a#a#b#b#c#c#b#b#a#a!,其实,在一般题目中,只要设一个起点就行了,终点的 \(!\)可以不用设,但是,在多测数据中,如果你直接写 scanf("%s", s); ,就会有坑!它只是将你输入部分所占的数组单元格的值给修改了,而其他单元格(也就是后面的单元格),如果之前输入了数据,那数据依然保留(说白了,就是 scanf("%s", s); \(\ne\) 清空数组),设个终点,可以防止出现各种稀奇古怪的错误(就因为这个,调了超过 \(3\) 小时的代码!)。
代码:
int change() {
int len = strlen(s);
int j = 2;
S[0] = '$', S[1] = '#';
for (int i = 0; i < len; ++ i) {
S[j ++] = s[i];
S[j ++] = '#';
}
S[j] = '!';
return j;
}
2、从前往后推半径
修改好字符串后,我们开始正式操作
先认识几个概念
半径 \(r\):以这个点为中点,在 \(r - 1\) 的范围内组成的字符串为回文串(为什么是 \(r - 1\) 而不是 \(r\)?因为中点也占一个单位),如下图
一个中点可能会有超过一条半径,我们这里取最大的半径,即取最长的回文串
最远位置 \(mx\):这个中点的最大回文串的右端点
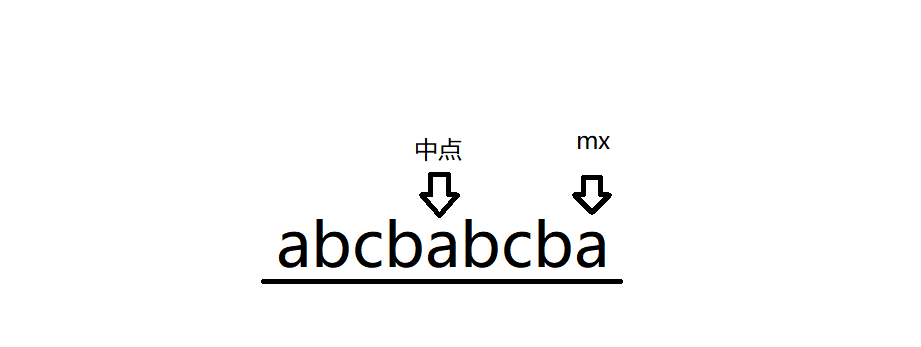
假设,我们要求以 \(i\) 为中点的最长回文串,我们设 \(j\) 为 \(i\) 点关于中点的对称点(\(j\) 在 \(i\) 的左边),我们是从左往右推的,\(j\) 就已经求过了,用 \(l_j\) 来表示 \(j\) 的半径。
现在 \(i\) 的情况有三种
一、\(i\) 的位置在 \(mx\) 之内,且 \(i + l_j < mx\)
在这种情况下,\(i\) 的半径 \(l_i =l_j\),为什么?看下面这张图

因为 \([mx',mx]\)(这里用 \(mx'\)来表示 \(mx\) 的对称点)是一个大的回文串,所以中点两边是对称的,如果以 \(j\) 点为中点的回文串被包括在这个大的回文串中且不越界,那么以 \(i\) 为中点的回文串肯定也包括在这个大的回文串中,而且位置与 \(j\) 的回文串对称,所以 \(l_i = l_j\)。
二、\(i\)的位置在 \(mx\) 之内,但 \(i + l_j > mx\)
这种情况就不同于之前的情况了,来看下面的图
我们可以看到,\(j\) 的回文串超出这个大的回文串了,说明 \(mx'\)左边的那一小部分与 \(j\) 的回文串中的最右边的部分相等,但是,\(mx'\) 左边的小部分因为不在回文串里,所以,\(mx\) 后边的等距离的部分与它不相等(如果相等,\(mx\) 就应该继续向右扩张),所以,对于 \(i\) 来说,它的半径不能超出 \(mx\),所以 \(i\) 的半径为 \(l_i = mx - i\)。
三、\(i\)的位置在 \(mx\) 外面
这种情况与前两种情况在本质上有不同(因为 \(i\) 的位置甚至不在大回文串内),\(i\) 可以说已经与大回文串没关系了,需要它自己去开辟新的回文串了,设\(l_i = 1\),然后自己去判断回文,同时也说明,这个大回文串的任务完成了,我们可以将中点移到 \(i\) 上,\(mx\) 的位置也要随之变化
这里我们解释一下为什么复杂度是 \(O_n\) 的,你会发现,\(mx\) 一直都是向右走,从不回头,只有要新开辟新的回文串时,\(mx\) 才会移动,对于一部分点,他们可以直接通过对称性 \(O_1\) 求出,剩下的就要慢慢扩展,但每次扩展,在新的回文串中的一部分点就又可以 \(O_1\) 查询答案了,最后均摊一下复杂度为 \(O_n\)解释的很烂,下面是度娘的解释
Manacher 算法的时间复杂度分析和 Z 算法类似,因为算法只有遇到还没有匹配的位置时才进行匹配,已经匹配过的位置不再进行匹配,所以对于 \(T\) 字符串中的每一个位置,只进行一次匹配,所以 Manacher 算法的总体时间复杂度为 \(O_n\),其中 \(n\) 为 \(T\) 字符串的长度,由于 \(T\) 的长度事实上是 \(S\) 的两倍,所以时间复杂度依然是线性的。——度娘
Z 算法就是扩展 KMP 算法
代码(核心代码):
int manacher() {
int len = change(), mid = 1, mx = 1, ans = -1;
for (int i = 1; i < len; ++ i) {
if (i < mx) {
l[i] = min(mx - i, l[(mid << 1) - i]);
// 这里将第一、二种情况合并了
}
else {
l[i] = 1;
// 对应第三种情况
}
while (S[i - l[i]] == S[i + l[i]]) { // 自己开发新回文串的过程
l[i] ++;
}
if (mx < i + l[i]) { // 更新中点与mx点
mid = i;
mx = i + l[i];
}
ans = max(ans, l[i] - 1);
// 注意,我们的回文串中有插入的符号#,所以总长度要取一半,也就是半径,又因为中点占了一个单位,所以要将中点的单位减去
}
return ans;
}
完整代码自己拼一下,可以写出来,实在写不出来一会会给你,最后,洛谷上有道模板题,可以去做一下,Manacher 算法一般会与其他的东西混用,如贪心、DP、Hash等等,只会板子还是不够的所以再扔三道题,HDU 4513、HDU 3948、BZOJ 3790$
记录自己的第一个字符串算法的博客!——\(2023.1.7\)
完整代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read() {
ll x = 0;
int fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? ~x + 1 : x;
}
const int N = 3e7;
char s[N], S[N];
int l[N];
int change() {
int len = strlen(s);
int j = 2;
S[0] = '$', S[1] = '#';
for (int i = 0; i < len; ++ i) {
S[j ++] = s[i];
S[j ++] = '#';
}
S[j] = '!';
return j;
}
int manacher() {
int len = change(), mid = 1, mx = 1, ans = -1;
for (int i = 1; i < len; ++ i) {
if (i < mx) {
l[i] = min(mx - i, l[(mid << 1) - i]);
// 这里将第一、二种情况合并了
}
else {
l[i] = 1;
// 对应第三种情况
}
while (S[i - l[i]] == S[i + l[i]]) { // 自己开发新回文串的过程
l[i] ++;
}
if (mx < i + l[i]) { // 更新中点与mx点
mid = i;
mx = i + l[i];
}
ans = max(ans, l[i] - 1);
// 注意,我们的回文串中有插入的符号#,所以总长度要取一半,也就是半径,又因为中点占了一个单位,所以要将中点的单位减去
}
return ans;
}
int main() {
scanf("%s", s);
printf("%d\n", manacher());
return 0;
}


