matplotlib

一、Matplotlib基础知识

Matplotlib中的基本图表包括的元素

• x轴和y轴 axis
  水平和垂直的轴线

• x轴和y轴刻度 tick
  刻度标示坐标轴的分隔，包括最小刻度和最大刻度

• x轴和y轴刻度标签 tick label
  表示特定坐标轴的值

• 绘图区域（坐标系） axes
  实际绘图的区域

• 坐标系标题 title
  实际绘图的区域

• 轴标签 xlabel ylabel
  实际绘图的区域

单个曲线图

 

 

 

 

 

 

 

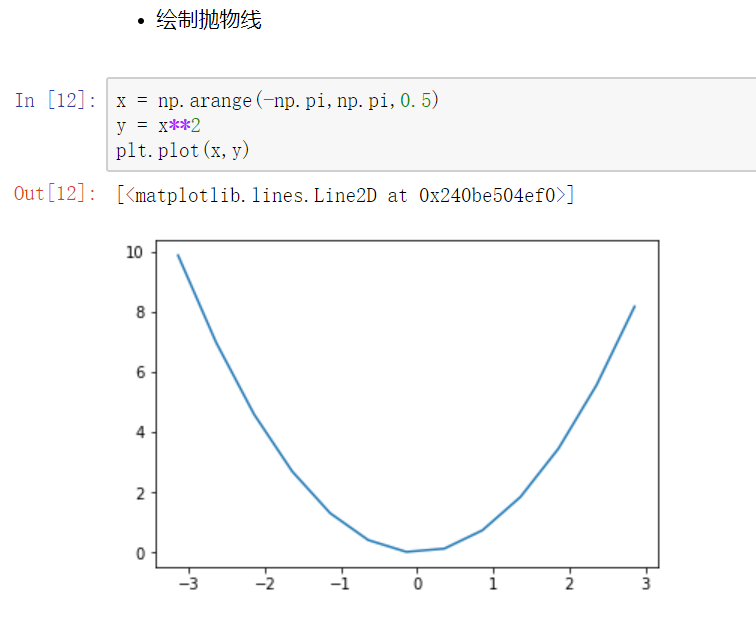
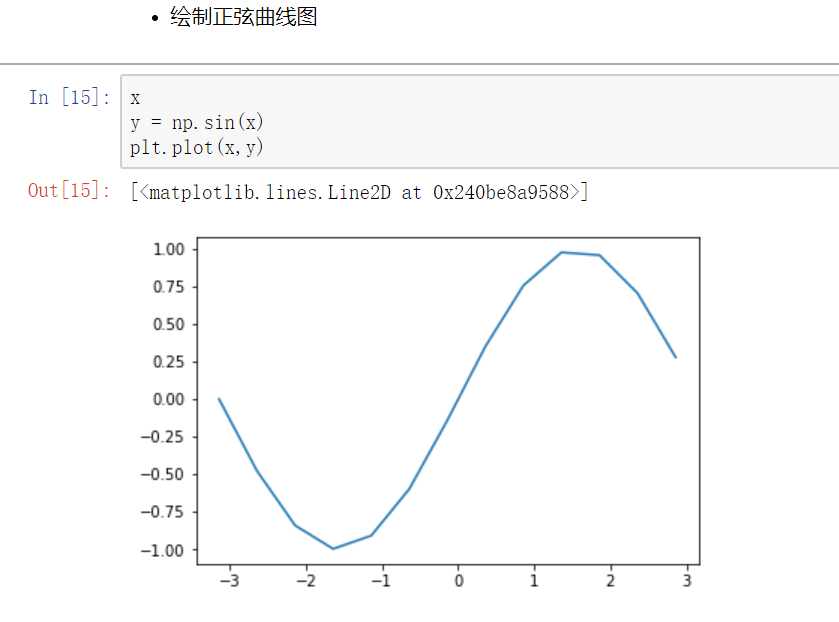
包含多个曲线的图

 1、连续调用多次plot函数

 

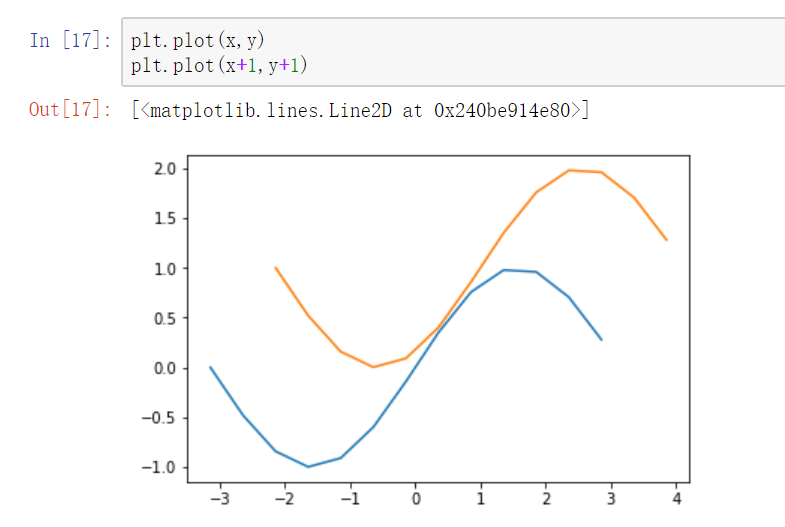
 2、也可以在一个plot函数中传入多对X,Y值，在一个图中绘制多个曲线

 

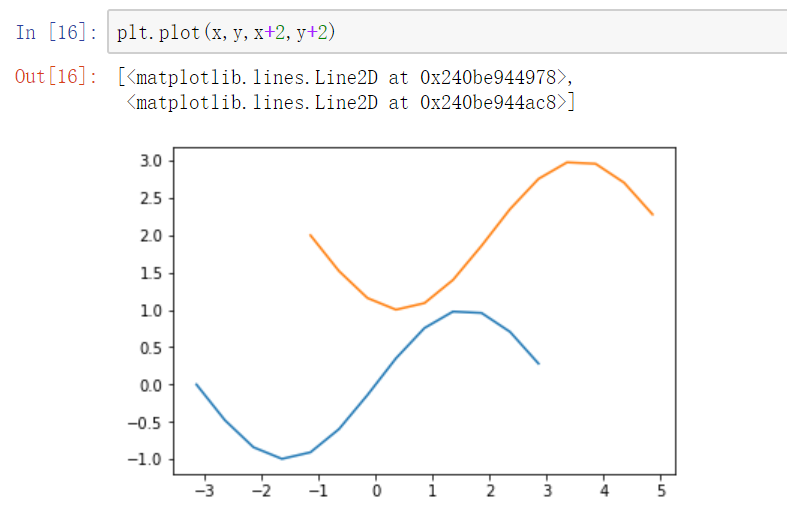
将多个曲线图绘制在一个table区域中：对象形式创建表图

• a=plt.subplot（row,col,loc） 创建曲线图
• a.plot(x,y) 绘制曲线图

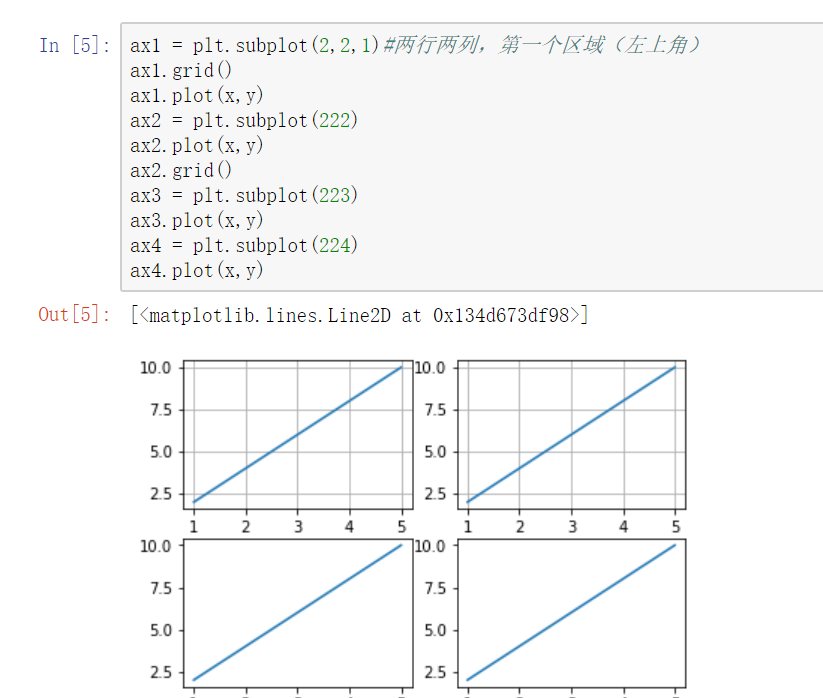
网格线 plt.gride(XXX)

参数：

- axis
- color:支持十六进制颜色
- linestyle: --  -.  :
- alpha

• 绘制一个正弦曲线图，并设置网格

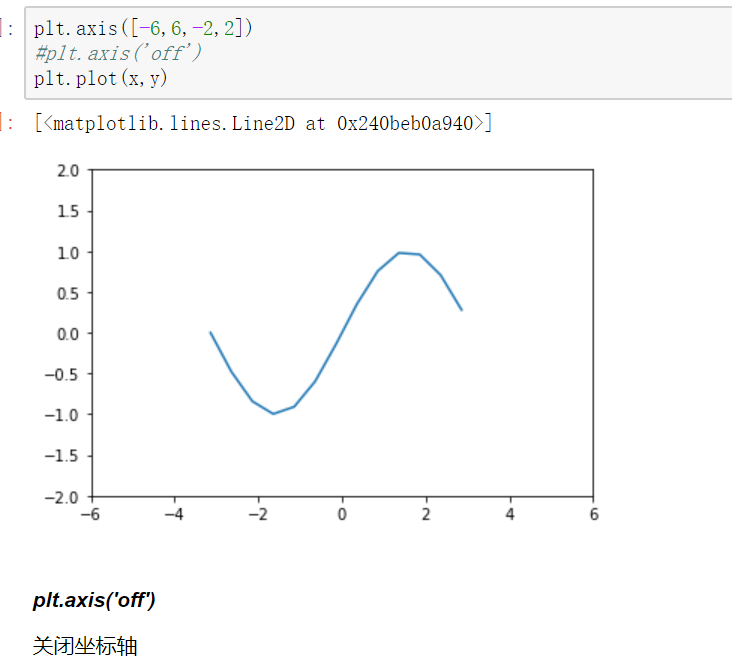
坐标轴界限

axis方法:设置x，y轴刻度值的范围

plt.axis([xmin,xmax,ymin,ymax])

 

 

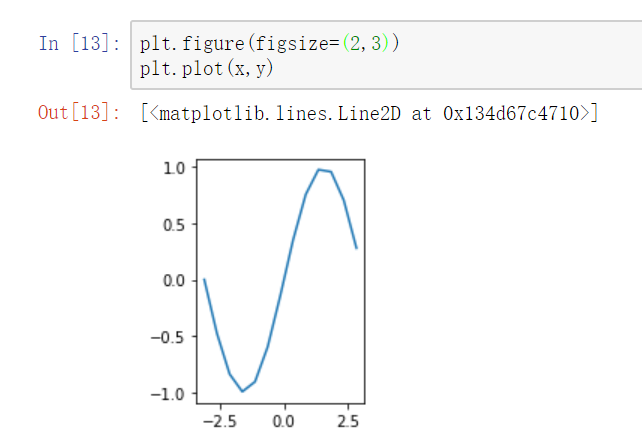
设置画布比例：plt.figure(figsize=(a,b)) a:x刻度比例 b：y刻度比例 （2:1）表示x刻度显示为y刻度显示的2倍

 

 

 

坐标轴标签

• s 标签内容
• color 标签颜色
• fontsize 字体大小
• rotation 旋转角度
• plt的xlabel方法和ylabel方法 title方法

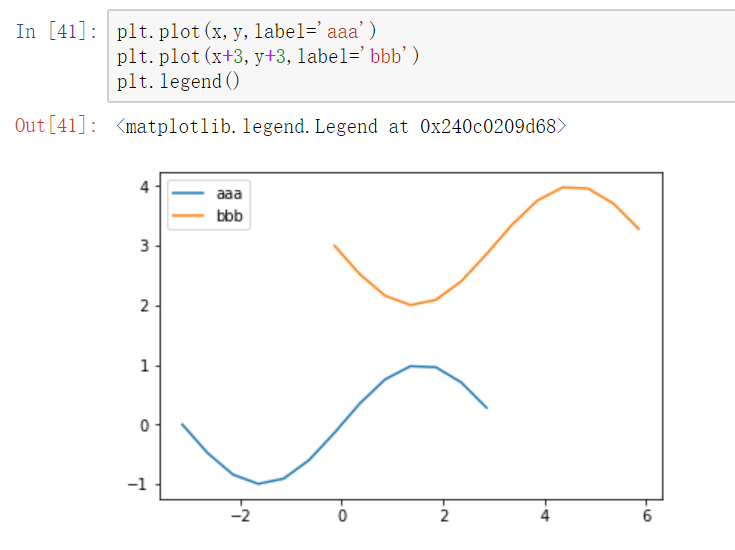
图例

legend方法

两种传参方法：

• 分别在plot函数中增加label参数,再调用plt.legend()方法显示
• 直接在legend方法中传入字符串列表

 

 

legend的参数

- loc参数

• loc参数用于设置图例标签的位置，一般在legend函数内
• matplotlib已经预定义好几种数字表示的位置

loc参数位置

 

 

 

 

 

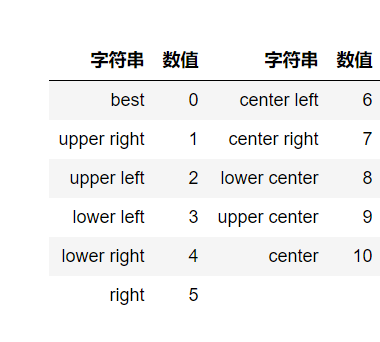
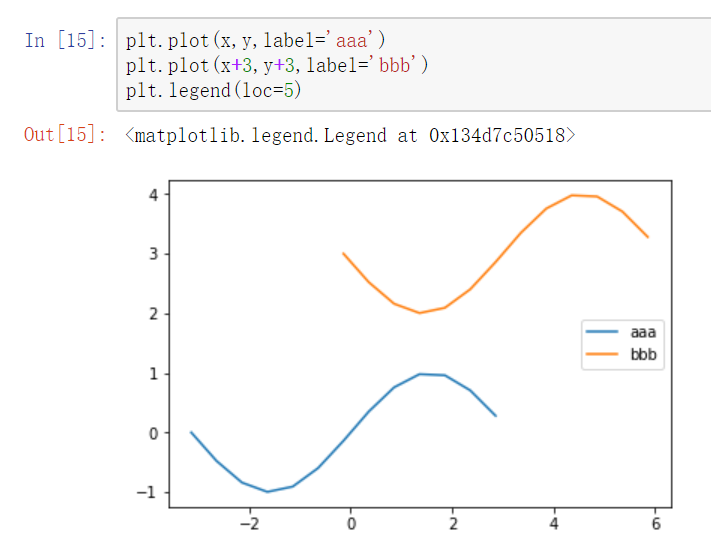
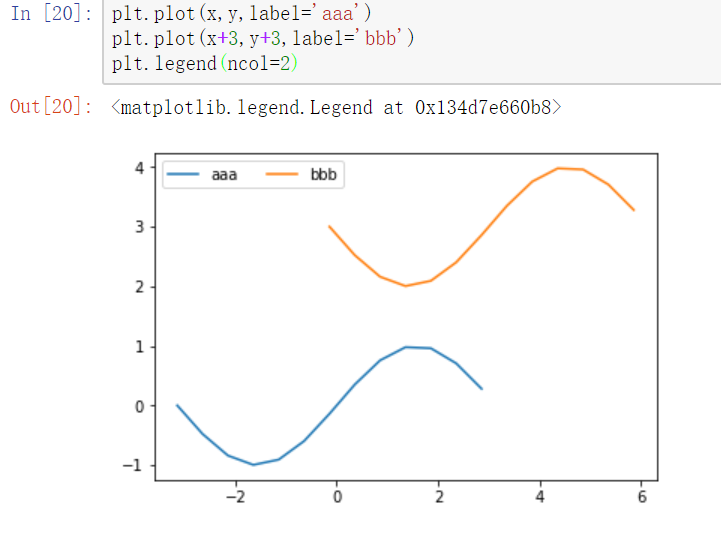
- ncol参数

ncol控制图例中有几列,在legend中设置ncol

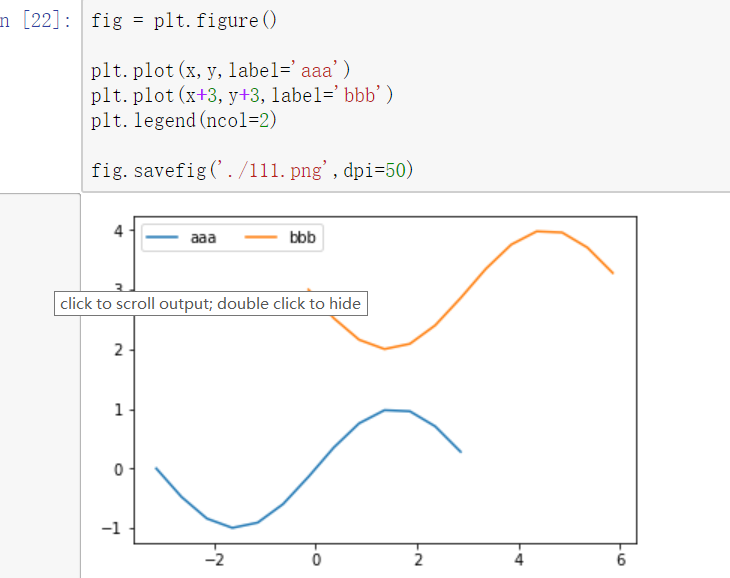
保存图片

使用figure对象的savefig函数来保存图片

fig = plt.figure()---必须放置在绘图操作之前

figure.savefig的参数选项

• filename
  含有文件路径的字符串或Python的文件型对象。图像格式由文件扩展名推断得出，例如，.pdf推断出PDF，.png推断出PNG （“png”、“pdf”、“svg”、“ps”、“eps”……）
• dpi
  图像分辨率（每英寸点数），默认为100
• facecolor ，打开保存图片查看 图像的背景色，默认为“w”（白色）

 

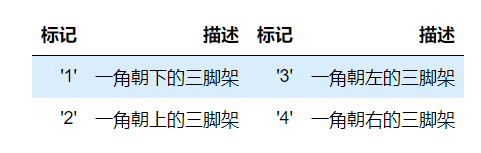
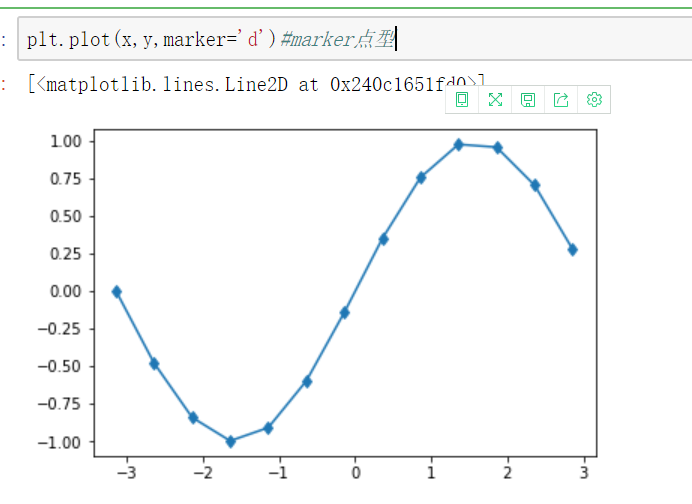
设置plot的风格和样式

plot语句中支持除X,Y以外的参数，以字符串形式存在，来控制颜色、线型、点型等要素，语法形式为：
plt.plot(X, Y, 'format', ...)

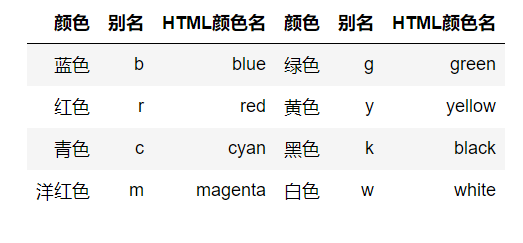
颜色

参数color或c

 

 

 

 

# 绘制线      plt.plot(x1,y1,x2,y2)
# 网格线      plt.grid(True)  axes.grid(color,ls,lw,alpha)
# 获取坐标系  plt.subplot(n1,n2,n3)
# 坐标轴标签  plt.xlabel() plt.ylabel()
# 坐标系标题  plt.title()
# 图例        plt.legend([names],ncol=2,loc=1)  plt.plot(label='name')
# 线风格      --  -. : None  step
# 图片保存    figure.savefig()
# 点的设置    marker markersize markerfacecolor markeredgecolor\width
# 坐标轴刻度  plt.xticks(刻度列表，刻度标签列表) plt.yticks()
#             axes.set_xticks(刻度列表) axes.set_xticklabels(刻度标签列表)

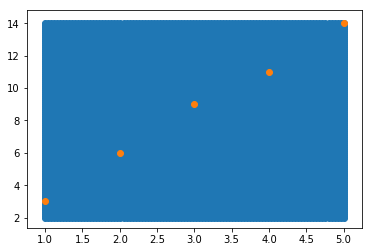
6、绘制散点图中的一个背景颜色

import numpy as np
import matplotlib .pyplot as plt 


# 设置足够多的连续的点
x = np.linspace(1,5,num=100)
y = np.linspace(2,14,num=100)

# 把所有点一一对应起来
xx,yy = np.meshgrid(x,y)

# 变形
xy = np.c_[xx.reshape(-1,1),yy.reshape(-1,1)]

# 画背景图
plt.scatter(xy[:,0],xy[:,1])

# 画散点图
a = [1,2,3,4,5]
b = [3,6,9,11,14]
plt.scatter(a,b)

三、2D图形

直方图

• 是一个特殊的柱状图，又叫做密度图。

【直方图的参数只有一个x！！！不像条形图需要传入x,y】

plt.hist()的参数

• bins
  直方图的柱数，可选项，默认为10
• color
  指定直方图的颜色。可以是单一颜色值或颜色的序列。如果指定了多个数据集合,例如DataFrame对象，颜色序列将会设置为相同的顺序。如果未指定，将会使用一个默认的线条颜色
• orientation
  通过设置orientation为horizontal创建水平直方图。默认值为vertical

 

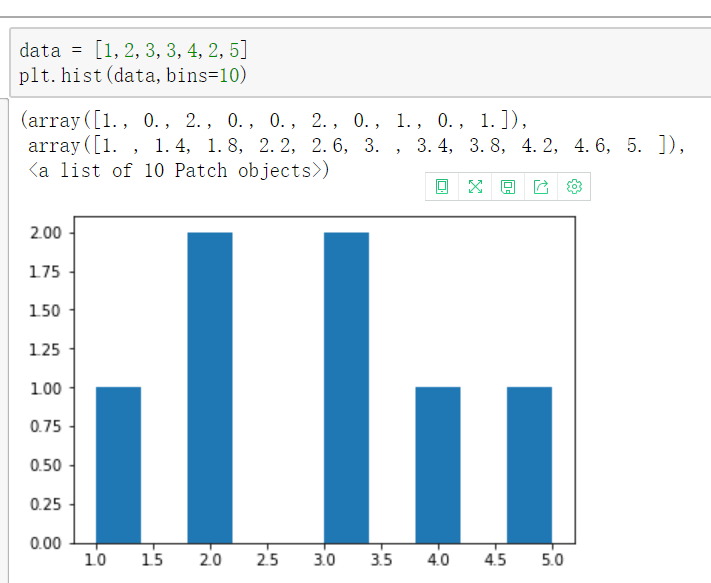
返回值 ：

1: 直方图向量，是否归一化由参数normed设定

2: 返回各个bin的区间范围

3: 返回每个bin里面包含的数据，是一个list

条形图：plt.bar()

• 参数：第一个参数是索引。第二个参数是数据值。第三个参数是条形的宽度

-【条形图有两个参数x,y】

• width 纵向设置条形宽度
• height 横向设置条形高度

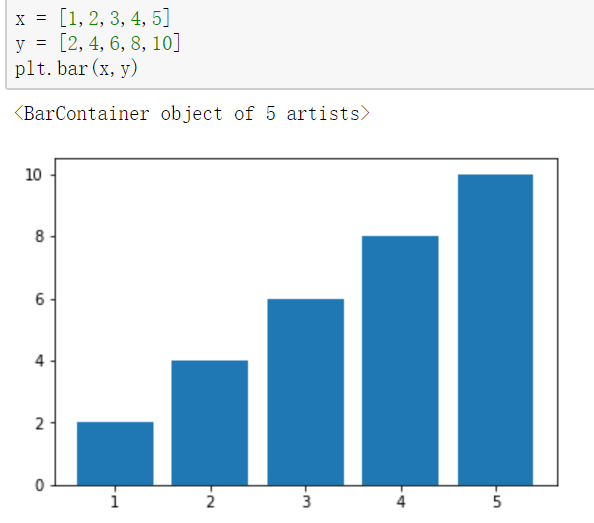
水平条形图

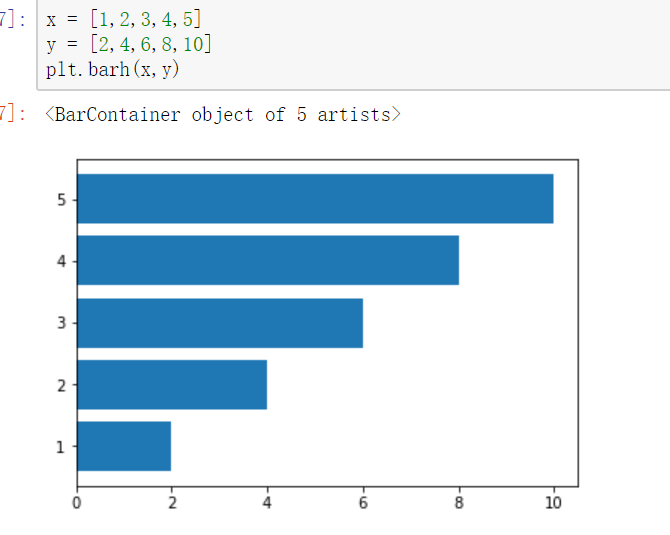
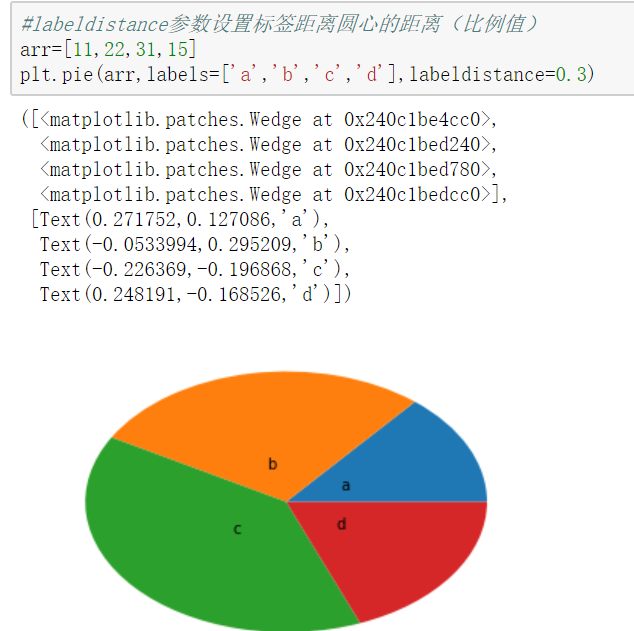
饼图

【饼图也只有一个参数x】

pie()
饼图适合展示各部分占总体的比例，条形图适合比较各部分的大小

 

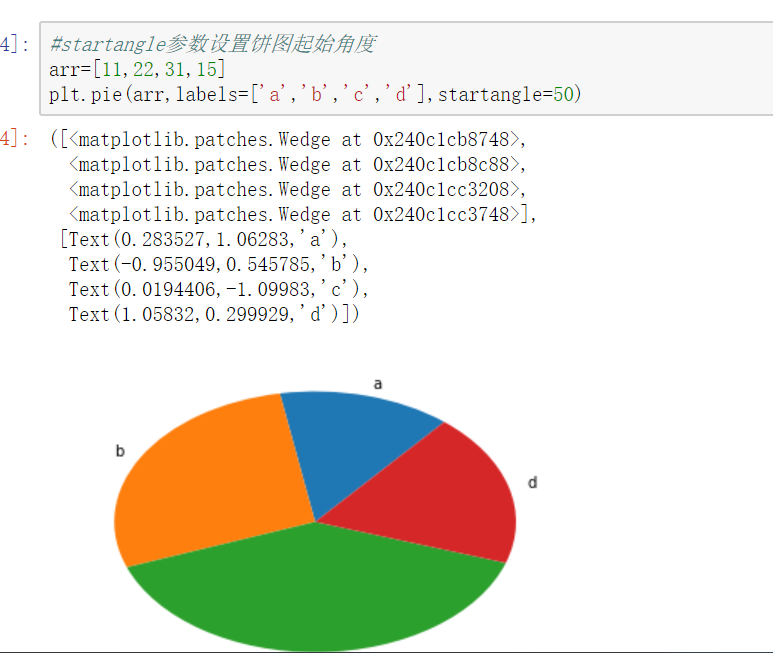
饼图阴影、分裂等属性设置

#labels参数设置每一块的标签；

#labeldistance参数设置标签距离圆心的距离（比例值）

#autopct参数设置比例值小数保留位(%.3f%%)； %m.nf m 占位 n 小数点后保留几位 f 是以float格式输出

#pctdistance参数设置比例值文字距离圆心的距离

#explode参数设置每一块顶点距圆心的长度（比例值,列表）；

#colors参数设置每一块的颜色（列表）；

#shadow参数为布尔值，设置是否绘制阴影

#startangle参数设置饼图起始角度

 

 

 

 

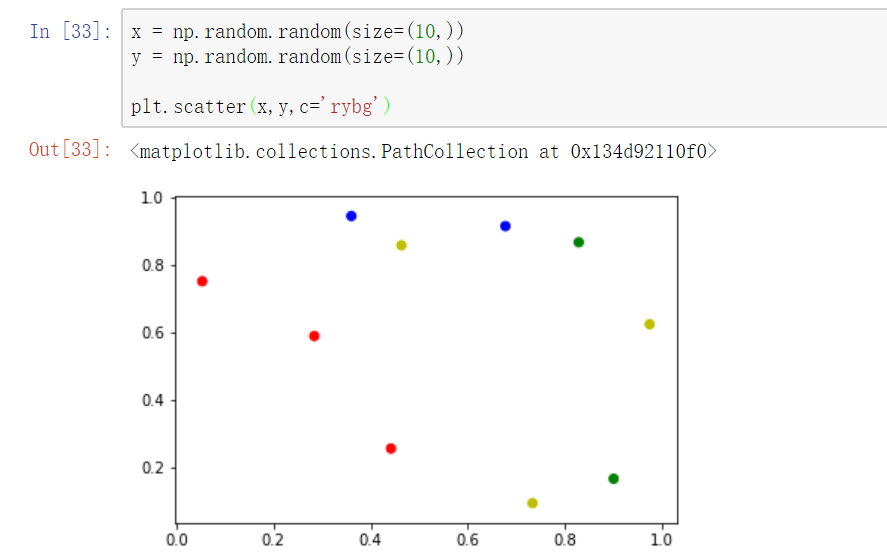
散点图：因变量随自变量而变化的大致趋势

散点图需要两个参数x,y，但此时x不是表示x轴的刻度，而是每个点的横坐标！

plt.scatter(x,y,marker='d',c="rbgy") 设置不同的散点颜色

 

案例分析：城市气候与海洋的关系研究

# 1.导入包
import numpy as np
import pandas as pd
from pandas import Series,DataFrame

import matplotlib.pyplot as plt
%matplotlib inline


from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题


# 2.导入数据各个海滨城市数据
# 导入并对每个城市的数据进行纵向级联匹配，生成10个DataFrame数据
ferrara1 = pd.read_csv('./ferrara_150715.csv')
ferrara2 = pd.read_csv('./ferrara_250715.csv')
ferrara3 = pd.read_csv('./ferrara_270615.csv')
ferrara=pd.concat([ferrara1,ferrara1,ferrara1],ignore_index=True)

torino1 = pd.read_csv('./torino_150715.csv')
torino2 = pd.read_csv('./torino_250715.csv')
torino3 = pd.read_csv('./torino_270615.csv')
torino = pd.concat([torino1,torino2,torino3],ignore_index=True) 

mantova1 = pd.read_csv('./mantova_150715.csv')
mantova2 = pd.read_csv('./mantova_250715.csv')
mantova3 = pd.read_csv('./mantova_270615.csv')
mantova = pd.concat([mantova1,mantova2,mantova3],ignore_index=True) 

milano1 = pd.read_csv('./milano_150715.csv')
milano2 = pd.read_csv('./milano_250715.csv')
milano3 = pd.read_csv('./milano_270615.csv')
milano = pd.concat([milano1,milano2,milano3],ignore_index=True) 

ravenna1 = pd.read_csv('./ravenna_150715.csv')
ravenna2 = pd.read_csv('./ravenna_250715.csv')
ravenna3 = pd.read_csv('./ravenna_270615.csv')
ravenna = pd.concat([ravenna1,ravenna2,ravenna3],ignore_index=True)

asti1 = pd.read_csv('./asti_150715.csv')
asti2 = pd.read_csv('./asti_250715.csv')
asti3 = pd.read_csv('./asti_270615.csv')
asti = pd.concat([asti1,asti2,asti3],ignore_index=True)

bologna1 = pd.read_csv('./bologna_150715.csv')
bologna2 = pd.read_csv('./bologna_250715.csv')
bologna3 = pd.read_csv('./bologna_270615.csv')
bologna = pd.concat([bologna1,bologna2,bologna3],ignore_index=True)

piacenza1 = pd.read_csv('./piacenza_150715.csv')
piacenza2 = pd.read_csv('./piacenza_250715.csv')
piacenza3 = pd.read_csv('./piacenza_270615.csv')
piacenza = pd.concat([piacenza1,piacenza2,piacenza3],ignore_index=True)

cesena1 = pd.read_csv('./cesena_150715.csv')
cesena2 = pd.read_csv('./cesena_250715.csv')
cesena3 = pd.read_csv('./cesena_270615.csv')
cesena = pd.concat([cesena1,cesena2,cesena3],ignore_index=True)

faenza1 = pd.read_csv('./faenza_150715.csv')
faenza2 = pd.read_csv('./faenza_250715.csv')
faenza3 = pd.read_csv('./faenza_270615.csv')
faenza = pd.concat([faenza1,faenza2,faenza3],ignore_index=True)


# 3.去除没用的列
cesena.head()  # 查看发现 Unnamed: 0 这一列是没用的数据

# 把每个df数据的 Unnamed: 0 这一列删除
city_list = [ferrara,torino,mantova,milano,ravenna,asti,bologna,piacenza,cesena,faenza]
for city in city_list:
    city.drop('Unnamed: 0',axis=1,inplace=True)


# 4.显示最高温度于离海远近的关系（观察多个城市）
city_max_temp = []  # 城市最高温度
city_dist = []  # 距海远近
for city in city_list:
    temp = city['temp'].max()
    dist = city['dist'].max()
    city_max_temp.append(temp)
    city_dist.append(dist)


# 5.绘制散点图
plt.scatter(city_dist,city_max_temp)
plt.xlabel('距离')
plt.ylabel('最高温度')
plt.title('距离和温度之间的关系')

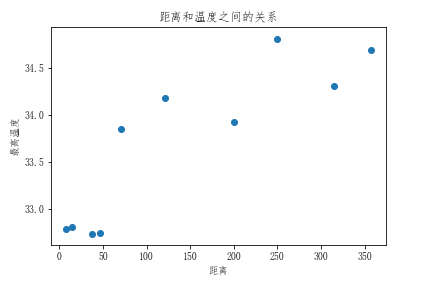
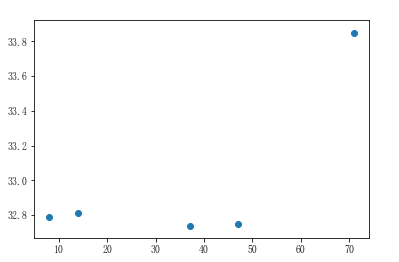
# 6.观察发现，离海近的可以形成一条直线，离海远的也能形成一条直线
# 分别以100公里和50公里为分界点，划分为离海近和离海远的两组数据(近海：小于100  远海：大于50)
city_dist = np.array(city_dist)  # 把python类型的数组转换成ndarray数组
city_max_temp = np.array(city_max_temp)

# 近海城市的温度和距离
condition = city_dist < 100
near_city_dist = city_dist[condition]
near_city_temp = city_max_temp[condition]

# 展示近海城市距离和温度的散点图
plt.scatter(near_city_dist,near_city_temp)

 

五、机器学习基础

•  样本数据：(df,np)
  　　特征数据：自变量(通常有多列，用二维数组展示)
  　　目标数据：因变量(通常只有一列，用一维数组展示)

• 算法模型：就是对象。在该对象中已经集成或者封装好了一种方程(还没有解的方程)，方程具有预测或者分类的功能
• 算法模型分类
  　　有监督学习：算法模型必须使用具有特征数据和目标数据的样本数据
  　　无监督学习：只需要特征数据的样本数据
         半监督学习：一部分需要特征数据和目标数据，一部分只需要特征数据

 样本数据和算法模型的关系：算法模型中的方程因没有数据所以是没有解的，想要解方程就需要样本提供的数据，解出来的结果就能够实现预测或者分类的功能

 python中算法模型都存在 sk_learn 这个模块中

 

 1、继续完善城市气候与海洋的关系研究的案例

1、继续完善城市气候与海洋的关系研究的案例

"""
代码是接着上面的案例
"""

# 1.导入sklearn，建立线性回归算法模型对象
from sklearn.linear_model import LinearRegression  # 导入线性回归算法模型
linner = LinearRegression()  # 实例化线性回归算法模型对象,即实例化了一个方程式：y=kx+b，此时没有数据，因此是无解的


# 2.训练模型：给模型提供数据，训练后的模型就已经有解了
# fit参数： X: 二维数组   y:一维数组
linner.fit(near_city_dist.reshape(-1,1),near_city_temp)
# 结果：LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)


# 3.给模型评分：查看这个模型的准确度
# 参数： X: 二维数组   y:一维数组
linner.score(near_city_dist.reshape(-1,1),near_city_temp)
# 结果：0.5549063263099332 代表有55%的几率预测成功


# 4.预测
# 模型已经有解了，用此方程进行预测
# 传入一个特征数据X(near_city_dist距离),返回一个预测到的结果(因变量)(near_city_temp温度)
linner.predict(60)  # 某个城市距离海洋60米，预测它的最高温度
# 结果：array([33.33408694]) 表示预测到这个城市的最高温度为33.33


# 5.批量预测
# 需要传入二维数组
linner.predict(np.array([60,70,75]).reshape(-1,1))
# 结果：array([33.33408694, 33.47477269, 33.54511557])

 

2、画出线性回归直线

# 画线性回归线
x = np.linspace(5,75,num=100)
y = linner.predict(x.reshape(-1,1))
plt.scatter(near_city_dist,near_city_temp)  # 近海城市的温度和距离
plt.scatter(x,y)  # 线性回归线

 

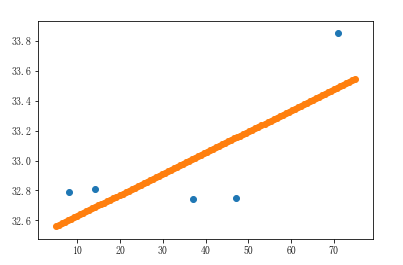
3、远海线性回归图

# 远海城市的温度和距离
far_condition = city_dist > 50
far_city_dist = city_dist[far_condition]
far_city_temp = city_max_temp[far_condition]

# 展示远海城市距离和温度的散点图
plt.scatter(far_city_dist,far_city_temp)

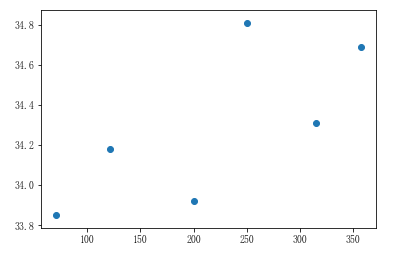
# 实例化线性回归算法模型对象,即实例化了一个方程式：y=kx+b，此时没有数据，因此是无解的
linner1 = LinearRegression()

# 训练模型：给模型提供数据，训练后的模型就已经有解了
# fit参数： X: 二维数组   y:一维数组
linner1.fit(far_city_dist.reshape(-1,1),far_city_temp)

# 给模型评分：查看这个模型的准确度
# 参数： X: 二维数组   y:一维数组
linner1.score(far_city_dist.reshape(-1,1),far_city_temp)
# 评分结果：0.5162479799447854

# 将远海城市的数据带入到散点图中进行展示，并且进行线性回归
x1 = np.linspace(50,400,100)
y1 = linner1.predict(x1.reshape(-1,1))
plt.scatter(far_city_dist,far_city_temp)
plt.scatter(x1,y1)

 

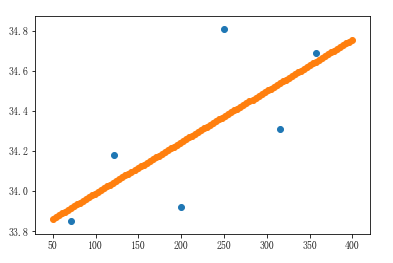
4、图例汇总

plt.scatter(city_dist,city_max_temp)  # 所有数据的散点图
plt.scatter(x,y)  # 近海的线性回归图
plt.scatter(x1,y1)  # 远海的线性回归图

 

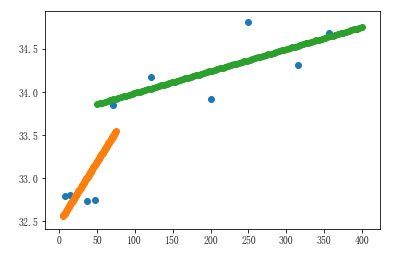
六、K-近邻算法（KNN）

众所周知，电影可以按照题材分类，然而题材本身是如何定义的?由谁来判定某部电影属于哪 个题材?也就是说同一题材的电影具有哪些公共特征?这些都是在进行电影分类时必须要考虑的问 题。没有哪个电影人会说自己制作的电影和以前的某部电影类似，但我们确实知道每部电影在风格 上的确有可能会和同题材的电影相近。那么动作片具有哪些共有特征，使得动作片之间非常类似， 而与爱情片存在着明显的差别呢？动作片中也会存在接吻镜头，爱情片中也会存在打斗场景，我们 不能单纯依靠是否存在打斗或者亲吻来判断影片的类型。但是爱情片中的亲吻镜头更多，动作片中 的打斗场景也更频繁，基于此类场景在某部电影中出现的次数可以用来进行电影分类。

这里介绍第一个机器学习算法：K-近邻算法，它非常有效而且易于掌握

 

简单地说，K-近邻算法采用测量不同特征值之间的距离方法进行分类。

• 优点：精度高(计算距离)、对异常值不敏感（单纯根据距离进行分类，会忽略特殊情况）、无数据输入假定（不会对数据预先进行判定）。
• 缺点：时间复杂度高、空间复杂度高。
• 适用数据范围：数值型和标称型。

 

1、工作原理

存在一个样本数据集合，也称作训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每一数据 与所属分类的对应关系。输入没有标签的新数据后，将新数据的每个特征与样本集中数据对应的 特征进行比较，然后算法提取样本集中特征最相似数据（最近邻）的分类标签。一般来说，我们 只选择样本数据集中前K个最相似的数据，这就是K-近邻算法中K的出处,通常K是不大于20的整数。 最后 ，选择K个最相似数据中出现次数最多的分类，作为新数据的分类。

 

回到前面电影分类的例子，使用K-近邻算法分类爱情片和动作片。有人曾经统计过很多电影的打斗镜头和接吻镜头，下图显示了6部电影的打斗和接吻次数。假如有一部未看过的电影，如何确定它是爱情片还是动作片呢？我们可以使用K-近邻算法来解决这个问题。

首先我们需要知道这个未知电影存在多少个打斗镜头和接吻镜头，上图中问号位置是该未知电影出现的镜头数图形化展示，具体数字参见下表

 

即使不知道未知电影属于哪种类型，我们也可以通过某种方法计算出来。首先计算未知电影与样本集中其他电影的距离，如图所示

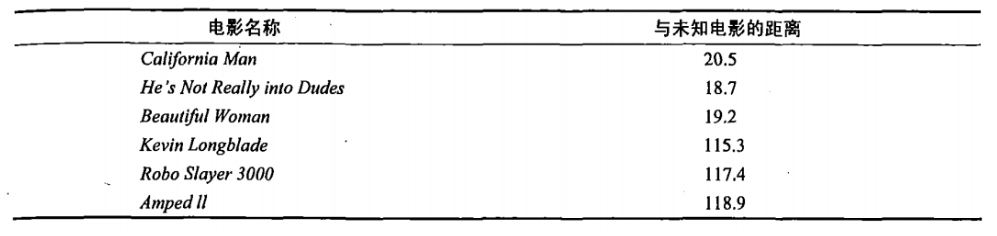
现在我们得到了样本集中所有电影与未知电影的距离，按照距离递增排序，可以找到K个距 离最近的电影。假定k=3，则三个最靠近的电影依次是California Man、He's Not Really into Dudes、Beautiful Woman。K-近邻算法按照距离最近的三部电影的类型，决定未知电影的类型，而这三部电影全是爱情片，因此我们判定未知电影是爱情片。

 

2、欧几里得距离(Euclidean Distance)

欧氏距离是最常见的距离度量，衡量的是多维空间中各个点之间的绝对距离。公式如下：

 

3、k-近邻算法案例

• 分类问题：from sklearn.neighbors import KNeighborsClassifier

1、一个最简单的例子

from pandas import DataFrame,Series
import numpy as np

dic = {
    '1身高':[160,175,177,165,180,163],
    '2体重':[50,70,72,67,76,51],
    '3鞋码':[37,41,41,40,43,38],
    '4性别':['女','男','男','男','男','女']
}

df = DataFrame(data=dic)

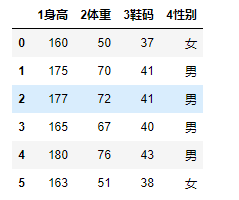
# 导入分类模型
from sklearn.neighbors import KNeighborsClassifier

# 实例化模型
knn = KNeighborsClassifier(n_neighbors=3)  # n_neighbors代表knn模型中的k值，也就是要取多少个邻近的数据

# 特征数据
feater = df.iloc[:,0:3]
targer = df.iloc[:,-1]
display(feater,targer)

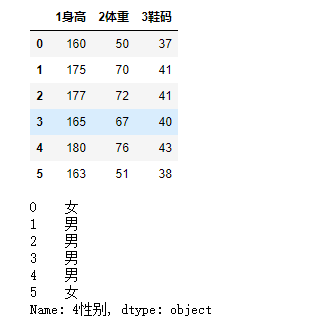
# 模型训练
knn.fit(feater,targer)

# 评分
knn.score(feater,targer)

# 预测
knn.predict(np.array([[160,55,37]]))
# 结果：array['女']

# 把原数据带进去预测
print('预测值：',knn.predict(feater))
print('真实值：',targer)

 

2、预测电影分类

from pandas import DataFrame,Series
import numpy as np
import pandas as pd

# 数据
df = pd.read_excel('../../my_films.xlsx')

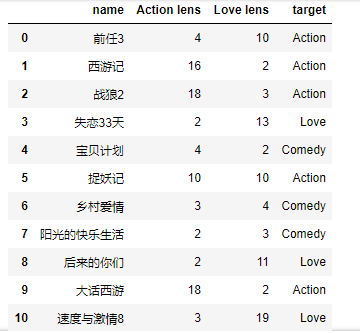
# 特征数据
feater = df.iloc[:,1:3]
targer = df.iloc[:,-1]

# 导入分类模型
from sklearn.neighbors import KNeighborsClassifier

# 实例化模型
knn = KNeighborsClassifier(n_neighbors=4)  # n_neighbors代表knn模型中的k值，也就是要取多少个邻近的数据

# 模型训练
knn.fit(feater,targer)

# 评分
knn.score(feater,targer)

# 预测
knn.predict(np.array([[60,45]]))
# 结果：array(['Action'], dtype=object)

 

七、sklearn的数据集-datasets

1、sklearn的数据集的介绍

sklearn.datasets模块主要提供了一些导入、在线下载及本地生成数据集的方法，主要有三种形式：load_<dataset_name>、fetch_<dataset_name>及make_<dataset_name>的方法。

1.datasets.load_<dataset_name>：sklearn包自带的小数据集

数据集文件在sklearn安装目录下datasets\data文件下

datasets.load_boston  # 波士顿房价数据集
datasets.load_breast_cancer  # 乳腺癌数据集
datasets.load_diabetes  # 糖尿病数据集
datasets.load_digits  # 手写体数字数据集
datasets.load_files
datasets.load_iris  # 鸢尾花数据集
datasets.load_lfw_pairs
datasets.load_lfw_people
datasets.load_linnerud  # 体能训练数据集
datasets.load_mlcomp
datasets.load_sample_image
datasets.load_sample_images
datasets.load_svmlight_file
datasets.load_svmlight_files

 

2.datasets.fetch_<dataset_name>：比较大的数据集，主要用于测试解决实际问题，支持在线下载

下载下来的数据，默认保存在~/scikit_learn_data文件夹下，可以通过设置环境变量SCIKIT_LEARN_DATA修改路径，datasets.get_data_home() 获取下载路径

datasets.fetch_20newsgroups
datasets.fetch_20newsgroups_vectorized
datasets.fetch_california_housing
datasets.fetch_covtype
datasets.fetch_kddcup99
datasets.fetch_lfw_pairs
datasets.fetch_lfw_people
datasets.fetch_mldata
datasets.fetch_olivetti_faces
datasets.fetch_rcv1
datasets.fetch_species_distributions

 

3.datasets.make_*?：构造数据集

datasets.make_biclusters
datasets.make_blobs
datasets.make_checkerboard
datasets.make_circles
datasets.make_classification
datasets.make_friedman1
datasets.make_friedman2
datasets.make_friedman3
datasets.make_gaussian_quantiles
datasets.make_hastie_10_2
datasets.make_low_rank_matrix
datasets.make_moons
datasets.make_multilabel_classification
datasets.make_regression
datasets.make_s_curve
datasets.make_sparse_coded_signal
datasets.make_sparse_spd_matrix
datasets.make_sparse_uncorrelated
datasets.make_spd_matrix
datasets.make_swiss_roll

 

2、基于datasets.load_iris鸢尾花数据集的案例

# 1.导入模块
import sklearn.datasets as datasets
import numpy as np
from sklearn.neighbors import KNeighborsClassifier

# 2.在sklearn.datasets数据集中获取数据
iris = datasets.load_iris()
iris  # 是一个大字典

# 3.提取样本数据
feature = iris['data']  # 特征数据
target = iris['target']  # 目标数据

# 4.将样本数据进行随机打乱
np.random.seed(10)
np.random.shuffle(feature)

np.random.seed(10)
np.random.shuffle(target)

# 5.查看数据的大小 
feature.shape  # (150, 4)
target.shape  # (150, )

# 6.获取训练样本数据和测试样本数据
# 前140条数据用做训练数据
x_train = feature[:140]
y_train = target[:140]

# 最后10条数据用做真实的测试数据
x_text = feature[-10:]
y_text = target[-10:]

# 7.实例化模型对象&训练模型
knn = KNeighborsClassifier(n_neighbors=15)
knn.fit(x_train,y_train)  # 训练数据

# 8.评分
knn.score(x_train,y_train)  # 0.9857142857142858

# 9.预测
print('预测分类结果：',knn.predict(x_text))
print('真实分类结果：',y_text)
# 预测分类结果： [0 1 0 2 2 2 1 0 2 0]
# 真实分类结果： [0 1 0 2 2 2 1 0 2 0]

 

八、手写数据识别案例

"""
图片数据在我的本地
"""

import numpy as np
import matplotlib .pyplot as plt 
from sklearn.neighbors import KNeighborsClassifier

# 1.查看单张图片的维度
img_arr = plt.imread('./data/3/3_3.bmp')
plt.imshow(img_arr)
img_arr.shape  # (28, 28)


# 2.导入本地数据，data和target都是5000个数据
feature = []
target = []
for i in range(10):
    for j in range(500):
        img_path = './data/'+str(i)+'/'+str(i)+'_'+str(j+1)+'.bmp'
        img_arr = plt.imread(img_path)
        feature.append(img_arr)
        target.append(i)

# 3.获得样本数据
feature = np.array(feature)  # 返回的是一个三维的数组
target = np.array(target)

# 4.将feature降成二维数组，才可以作为模型的特征数据
feature = feature.reshape(5000,-1)

# 5.打乱样本数据
np.random.seed(1)
np.random.shuffle(feature)
np.random.seed(1)
np.random.shuffle(target)

# 6.提取训练和测试数据
x_train = feature[:4950]  # 训练数据
y_train = target[:4950]

x_test = feature[-50:]  # 测试数据
y_test = target[-50:]


# 7.实例化模型，训练模型
knn = KNeighborsClassifier(n_neighbors=15)
knn.fit(x_train,y_train)
knn.score(x_train,y_train)  # 0.9357575757575758

# 8.测试
print('预测分类：',knn.predict(x_test))
print('真实分类：',y_test)

# 结果
预测分类： [0 7 5 2 3 6 3 0 5 9 9 7 2 2 1 9 8 0 1 5 5 2 7 5 8 2 2 3 7 7 1 6 5 1 9 9 0 5 5 8 7 6 5 8 0 5 5 1 7 0]
真实分类： [0 7 5 2 3 6 3 0 5 9 9 7 2 2 1 9 8 0 1 8 5 2 7 5 8 2 2 3 7 3 1 6 5 1 9 7 0 5 5 8 2 6 5 8 0 5 5 1 7 0]

 

用上面的模型，预测一张图里的数字

# 使用外部图片对模型进行测试
num_arr = plt.imread('./数字.jpg')
plt.imshow(num_arr)

# 切片，把数字 5 切出来
five = num_arr[90:150,85:130]
plt.imshow(five)

# 查看这张图片的维度
five.shape  # (60, 45, 3)，其中60、45是它的像素，3是颜色

# 降维
# 不能用reshape，因为我们需要的是(60,45)像素，而不是(60,45*3)
five = five.mean(axis=2)
five.shape  # (60, 45)

# 把降维后的图片压缩成28*28,因为我们模型的维度就是(28,28)
import scipy.ndimage as ndimage
five = ndimage.zoom(five,zoom=(28/60,28/45))
five.shape  # (28, 28)

# 查看特征数据的维度
feature.shape  # (5000, 784)

# 把要预测的二维数组变形成一致的形状进行预测
knn.predict(five.reshape(1,784))
# 结果
array([5])  正确预测出

 

 保存模型

# 保存模型
from sklearn.externals import joblib
joblib.dump(knn,'./digist_knn.m')  # dump(模型,路径)


# 要使用的时候直接导入模型
knn = joblib.load('./digist_knn.m')