【算法】贪心算法
一、算法理解
所谓贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,它所做出的仅是在某种意义上的局部最优解。也就是说在每一步中,选择目前最优的策略,而不考虑全局是不是最优的。
贪心算法的前提:
1、 原问题复杂度过高
2、 求全局最优解的数学模型难以建立
3、 求全局最优解的计算量过大;
4、 没有太大必要一定要求出全局最优解,“比较优”就可以。
贪心算法没有固定的算法框架,算法设计的关键是 贪心策略 的选择。必须注意的是,贪心算法不是对所有问题都能得到整体最优解,选择的贪心策略必须具备 无后效性,即 某个状态以后的过程不会影响以前的状态 ,只与当前状态有关。所以对所采用的贪心策略一定要仔细分析其是否满足无后效性。
贪心算法实现步骤:
- 建立数学模型来描述问题。
- 把求解的问题分成若干个子问题。
- 对每一子问题求解,得到子问题的局部最优解。
- 把子问题的解局部最优解合成原来解问题的一个解。
实现该算法的过程:
从问题的某一初始解出发;
while (能朝给定总目标前进一步)
{
利用可行的决策,求出可行解的一个解元素;
}
由所有解元素组合成问题的一个可行解;
贪心算法存在的问题
- 算法存在的问题 不能保证 求得的解是 整体最优 的;
- 不能用来求最大值或者最小值的问题;
- 只能求满足某些约束条件下的可行解的范围。
求解问题的分解方式
按串行任务分 时间串行的任务,按子任务来分解,即每一步都是在 前一步的基础上再选择当前的最优解 。 按规模递减分 规模较大的复杂问题,可以借助 递归思想,分解成一个规模小一点点的问题,循环解决,当最后一步的求解完成后 就得到了所谓的“全局最优解”。 按并行任务分 问题的任务不分先后,可能是并行的,可以分别求解后,再按一定的规则(比如某种配比公式)将其组合后得到最 终解。
适用场景
适用贪心算法的问题通常具备两个性质:
1、 贪心选择性质:所求问题的 整体最优解可以通过一系列局部最优的选择来得到。一般需要进行多步的贪心选 择。每经过一次贪心选择后,原问题变成一个规模更小的相似的问题,而后每一步都做当前最佳的选择,且每一个 选择都仅作一次。
2、 最优子结构性质:一个问题的最优解包含子问题的最优解,比如在部分背包问题中,第一次选择单位重量价值 最大的物品,它是第一个子问题的最优解,第二次选择剩下的物品中单位价值最大的物品,是第二个子问题的最优 解,依次类推。 贪心算法通常使用 自顶向下 的方式做出一系列贪心选择。典型的问题包括货币选择问题、部分背包问题、活动选择 问题、哈夫曼编码问题、最小生成树问题、单源最短路径问题、作业排序问题等
四、使用案例
1)背包问题
【算法描述】
使用贪心算法解决该类问题就是要将每次的物品放入看成一步,并且每一步都放入最优解,用x(i)表示第i个物体加入背包。
此问题的约束条件为所选物体放入背包后,重量不超过W,因此需要满足,物品重量(KG) 价值(元) 单位价值
1 18 36 2 2 15 45 3 3 10 40 4 此问题可选择的贪心维度有重量、价值、单位价值:
-
重量小优先
物品1:重量1KG,价值10元
物品2:重量2KG,价值50元
背包总重:2KG
根据策略,先取物品1,再取物品2中的1KG,总价值为10+25=35元。
如果先取物品2,总价值为50元>35元, 因此该策略不可用。 -
价值高优先
物品1:重量1KG,价值40元
物品2:重量2KG,价值50元
背包总重:2KG
根据策略,先取物品2,总价值为50元。
如果先取物品1,再物品2,总价值为40+25=65元>50元。
因此该策略不可用。 -
单位价值高优先
物品1:重量1KG,价值40元
物品2:重量2KG,价值50元
背包总重:2KG
物品1单位价值为40元,物品2单位价值为25元。
根据策略,先取物品1,再取物品2,总价值为40+25=65元,为最优解。
因此优先选择单位重量下价值最大的物品(贪心策略)。
算法说明:假设背包总重量为30KG,物品信息如下,
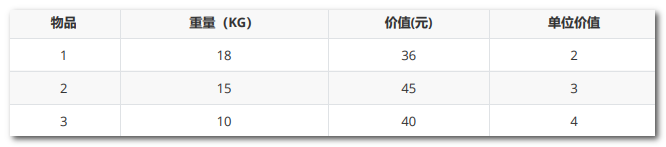
按照贪心策略,单位重量的价值排序为:物品3>物品2>物品1。 最终选择为物品3全部、物品2全部以及物品1中5KG。
3)[用最少数量的箭引爆气球]
力扣:https://leetcode-cn.com/problems/minimum-number-of-arrows-to-burst-balloons/
【思路】LeetCode
如果不将数组排序,讨论起来过于复杂。于是先按照 左值大小排序。
从第一个元素开始比较,如果后一个元素的左值小于等于前一个元素的右值则表示该求可以纳入一箭之中。
同时我们也注意到这样讨论存在局限性如:[1,3],[1,2],[3,4] 答案本因是2,却输出1,原因就是后一个元素应该与前面一箭的元素右值最小值比较(短板效应)而不是第一个元素,因此每次将一个气球收纳起来时应该将被比较值更新为前一箭右值最小者和该气球右值中的较小者。
具体思想:
- 第一个元素的右值设置为被比较值 kef
- 将待检测元素L的左值和右值分别记录为 right 和 left
- 当kef大于left表示这个气球可以被刺穿,同时比较right和kef的大小(短板效应)将二者中较小的一个设置为kef继续比较
class Solution
{
public:
int findMinArrowShots(vector<vector<int>>& points)
{
//排除这些乱七八糟的干扰
int size = points.size();
if (size <= 1)
return size;
//按照左值从小到大排序
sort(points.begin(), points.end());
//kef初始化为第一行右值
int kef = points[0][1];
int begin = 1;
int ssort = 0;
int left;
int right;
while (begin < size)
{
left = points[begin][0];
right = points[begin][1];
if (left > kef)
{
ssort++;
kef = right;
}
else
kef = (kef > right ? right : kef);
begin++;
}
//不管什么情况最后都有一只剑没有计算上去
ssort++;
return ssort;
}
};




