【算法】动态规划
一、算法理解
【基本概念】:
动态规划(dynamic programming),就是对原问题分解,分解成子问题,通过解决子问题从而解决原问题。动 态规划应用于 子问题重叠的情况(分而治之方法子问题独立不相交),即 不同子问题具有公共的子问题 。动态规 划通过对子子问题的求解然后保存求解结果,从而无需每次都对子子问题重新计算。 动态规划方法通常使用求解 最优化 问题。这类问题可以有很多可行的解,每个解都有一个值,我们希望寻找最优的 值如最小值或最大值的解,我们称这样的解为问题的一个最优解(an optimal solution),这里求解的只是最优解 (the optimal solution)中的一个,因为最优解可能有多个。
适用动态规划的问题必须满足最优化原理、无后效性和重叠性。
1)最优化原理(最优子结构性质):最优化原理可这样阐述:一个最优化策略具有这样的性质,不论过去状态和 决策如何,对前面的决策所形成的状态而言,余下的决策必须构成最优策略。简而言之,一个最优化策略的子策略 总是最优的。更通俗一些讲:如果一个问题的解是最优的,那么该问题分解出的子问题,子问题的解也是最优的。 一个问题满足最优化原理又称其具有最优子结构性质。
可以这样反证:一个问题x的最优解为f(x),f(x)由1到K个子问题组成(K>=1),假设各子问题x1 ~ xK各自的最优 解:f(x1) ~ f(xK)组成了x的最优解f(x),所有子问题都是最优的那么该问题f(x)一定是最优的 。
2)无后效性:将各阶段按照一定的 次序排列 好之后,对于某个给定的阶段状态,它 以前各阶段 的状态无法直接影响它未来的决策,而只能通过当前的这个状态。换句话说,每个状态都是过去历史的一个完整总结,不会影响后继状态 。这就是无后向性,又称为无后效性。
3)子问题的重叠性:一个问题可分解成子问题求解,如果该问题用递归方法求解,会反复求解相同子问题而不是一直生成新的子问题,那么就称该最优化问题具有重叠子问题的性质,即子问题的重叠性。 动态规划将原来具有指数级时间复杂度 的算法改进成了 具有多项式时间复杂度 的算法。其中的关键在于解决冗余即 不必要的重复计算,这是动态规划算法的根本目的。动态规划实质上是一种以 空间换时间 的算法,它在实现的过程中,不得不 存储过程中产生的各种状态 ,所以它的空间复杂度要大于其它的算法。所以如果一个问题的子问题 不具有重叠性,那么使用动态规划没有降低时间复杂度,反而提高了空间复杂度,为何要用它,或者说还能称为动态规划算法?
三、使用案例
0)0~1背包问题
下面以0-1背包问题来做讲解。 有N件物品和一个容量为V的背包。第i件物品的重量是 weight[i] ,价值是 value[i] 。求解将哪些物品装入背包可使价值总和最大。 这些物品各只有一件,要么选择放入背包要么选择不放,所以称为0-1背包。
一、前面解法:计算物品密度,按照密码从小到大逐个排序。
二、动态规划的思路
(1)自顶而下方法
我们假设最优解使用数学函数f(i, j)表示,其含义就是前i件物品装入容量为j的背包总价值最大值,其中变量i和j的取值范围:0<=i<=N,0<=j<=V。
对f(i, j)问题进行子问题分解:
- 子问题1:如果当前物品i不装入背包,由f(i, j)逆推子问题1:f(i-1, j),不装入背包的理由可能是j的空间装不下i,也可能是能装的下但是装入后的值不一定最优。
- 子问题2:如果当前物品i装入背包,由f(i, j)逆推子问题2:f(i-1, j-weight[i])。
- f(i, j)究竟取f(i-1, j)还是取f(i-1, j-weight[i])+value[i]则看这两个表达式谁最大。 所以有f(i, j) = max(f(i-1, j), f(i-1, j-weight[i])+value[i]),这个我们称之为0-1背包的状态方程。
- 再次:对f(i, j) 的i、j取值的边界进行细化处理:i = 0即没有物品装入背包,背包中物品价值为0;j = 0即背包容量 是0则背包物品价值为0,即f(0, j) = f(i, 0) = 0。
【源码参考】:
public int topDownZeroOnePackage(int[] weight, int[] value, int n, int packageWeight) {
// 物品数量为0,背包容量为0,价值为0
if (n == 0 || packageWeight <= 0) {
return 0;
}
else if (n > 0 && packageWeight < weight[n]) {
return topDownZeroOnePackage(weight, value, n-1, packageWeight);
}
else if (n > 0 && packageWeight >= weight[n]) {
int maxValue = max(topDownZeroOnePackage(weight, value, n-1, packageWeight), value[n]
+ topDownZeroOnePackage(weight, value, n-1, packageWeight-weight[n]));
return maxValue;
}
else {
return 0;
}
}
上述递归处理,每件物品处理时都会出现要么放入背包、要么不放入背包,所以每件物品的处理最多都有两种选择,所以对n件物品处理最多有2n种选择。所以T(n) = O(2n),一旦物品数n过大、会出现性能瓶颈。
逻辑简化后变成:
public int topDownZeroOnePackage(int[] weight(物品重量数组), int[] value(物品价值数组), int n(第n各商品), int packageWeight(剩余容量)) {
// 物品数量为0,背包容量为0,价值为0
if (n == 0 || packageWeight <= 0) {
return 0;
}
// 程序走到这里时已经能够确保n>0, packageWeight>0
int maxValue = topDownZeroOnePackage(weight,value,n-1,packageWeight);
if (packageWeight >= weight[n]) {
maxValue = max(maxValue, value[n]
+ topDownZeroOnePackage(weight, value, n-1, packageWeight-weight[n]));
}
return maxValue;
}
优化:带备忘录的递归实现
我们解决一个问题比如 f(i,j) , f(i,j) 的子问题是 f(i-1,j) , f(i-1,j-weight(i)) 以
此类推,问题的子问题可能存在重叠,而计算过程中没有保存子问题的求解的结果,导致重叠的子问题被反复求
解,浪费机器算力。所以通过保存子问题求解结果,一旦求解子问题,先搜索子问题求解结果,如果存在则不必求
解,直接获取保存的结果,可以优化掉重叠子问题的重复求解。
源码参考
// 数组大小定义为n和packageWeight,因为最终求的是f(n, packageWeight)。PS:f(0, ?)都为0,f(?, 0)都为0
int[][] m_memo = new int[n + 1][packageWeight + 1];
public int topDownZeroOnePackageWithMemoEnter(int[] weight,int[] value,int n,int packageWeight){
for (int i = 0; i <= n; i++) {
for(int j = 0;j <= packageWeight;j++) {
m_memo[i][j] = -1;
}
}
return topDownZeroOnePackageWithMemo(weight, value, n, packageWeight);
}
public int topDownZeroOnePackageWithMemo(int[] weight,int[] value,int n,int packageWeight) {
// 物品数量为0,背包容量为0,价值为0
if (n == 0 || packageWeight <= 0) {
return 0;
}
// 子问题已经被计算过就不需要再计算
if (m_memo[n][packageWeight] != -1) {
return m_memo[n][packageWeight];
}
// 程序走到这里时已经能够确保n>0, packageWeight>0
int maxValue = topDownZeroOnePackage(weight,value,n-1,packageWeight);
if (packageWeight >= weight[n]) {
maxValue = max(topDownZeroOnePackage(weight, value, n-1, packageWeight), value[n]
+ topDownZeroOnePackage(weight, value, n-1, packageWeight-weight[n]));
}
m_memo[n][packageWeight] = maxValue;
return maxValue;
}
(2)自底而上方法
对于0-1背包问题的状态方程为:
1) f(i,0) = f(0,j) = 0 条件: i = 0 或 j = 0 ,即背包容量是0或没有物品放入则最大价值是0。
2) f(i,j) = f(i-1, j) , j < weight(i) ,背包剩余容量 j 小于第 i 件物品的容量,第 i 件物品无法装入背
包。
3) f(i,j) = max(f(i-1,j), f(i-1,j-weight(i)) + value(i)) , i > 0,j >= weight(i) ,背包剩余容量j
大于物品i的容量。装入还是不装入看 f(i-1,j), f(i-1,j-weight(i)) + value(i) 哪个价值大。
通用状态方程为 f(i,j) = max(f(i-1,j), f(i-1,j-weight(i)) + value(i))。
f(i,j) 的最大值就是找到 f(i,j) 的子问题的最大值,而 f(i,j) 的变化有两个维度 i 和 j ,所以 f(i,j)
的子问题值可以展开使用二重循环来实现,T(n) = O(N x V),动态规划把可能的指数求解时间转换成多项式的时间。
- 对于外层循环(主循环)i 从1开始逐渐增大,即从小到大循环,这主要因为要先求出问题的子问题然后才能求出问题。
- 而对于内层循环则无所谓,不论内层循环j从大到小,还是从小到大都可以,当然内层循环从小到大更容易理解些,因为都是先求出子问题再求出问题。
而内层循环从大到小可以这样理解:外层循环每循环一次,内层循环结束后,计算的结果输出一行子问题解,外层循环下一次循环行时:
f[i]/[j] = max(f[i-1]/[j], f[i-1]/[j-weight[i]] + value[i]) 不论 f[i-1]/[j] 还是 f[i-1]/[j-weight[i]] 都是上一次外层循环计算出的子问题的结果,所以当前外层循环要计算的问题,依赖的上一次外层循环计算出各子问题,上次外层循环已经计算出了子问题的确定值,所以本次外层循环时,内层循环从大到小也可以计算出问题的确定值。
源码参考:
public int bottomUpZeroOnePackage(int[] weight, int[] value, int n, int packageWeight) {
// 初始化成0 如果初始化成-1, 时packageWeight = 0会得到-1的解
int[][] m_memo = new int[n + 1][packageWeight + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= packageWeight; j++) {
m_memo[i][j] = 0;
}
}
for (int i = 1; i<=n; i++) {
// 或者for(int j = packageWeight; j >= 1; j--) 内层循环从大到小循环也可以
for (int j = 1; j <= packageWeight; j++) {
m_memo[i][j] = m_memo[i - 1][j];
if (j >= weight[i]) {
m_memo[i][j] = max(m_memo[i - 1][j], value[i] + m_memo[i - 1][j - weight[i]]);
}
}
}
return m_memo[n][packageWeight];
}
优化:空间优化
对于所有子问题保存于 m_memo(n+1, packageWeight+1) 二维数组中,这个还可以进一步做空间优化,从状态方程f(i,j) = max(f(i-1, j) ,f(i-1,j-weight(i)) + value(i)) 可以看出,每个问题 f(i, j) 的计算只直接依赖于f(i-1, j) 或 f(i-1, j-weight(i)) + value(i) ,即只依赖上一次外层(j-1)循环计算出的子问题,所以每次只保存上一次外层循环计算的子问题的值就可以了,所以只要用一维数组 memo(packageWeight + 1) 就可以实现。不用像m_memo(n+1, packageWeight+1) 保存各个循环计算的所有子问题的值。
public int bottomUpSpaceOpsZeroOnePackage(int[] weight, int[] value, int n, int packageWeight) {
// 初始化成0 如果初始化成-1时packageWeight=0会得到-1的解
int[] memo = new int[packageWeight + 1];
for (int j = 0;j <= packageWeight;j++) {
memo[j] = 0;
}
for (int i = 1; i <=n; i++) {
for (int j = packageWeight; j >= 1; j--) {
if (j >= weight[i]) {
memo[j] = max(memo[j], value[i] + memo[j - weight[i]]);
}
}
}
return memo[packageWeight];
}
【初始值问题】
问题、子问题存储空间值的初始化问题:
上述背包问题,只是要求背包装不下为止,装入背包的物品价值之和最大。如果要求装入背包的物品,恰好装满背包,装入背包的物品价值之和最大,如何解?
- 看一下不要求恰好装满背包的状态方程:
1) f[i][0] = f[0][j] = 0 条件: i = 0 或 j = 0 。
2) f[i][j] = f[i-1][j] , j < weight[i] 。
3) f[i][j] = max(f[i-1][j], f[i-1][j-weight[i]] + value[i]) , i > 0,j >= weight[i]
不要求恰好装满背包,最终求出的结果可能两种情况:
1)背包恰好装满,问题分解出的子问题最终会分解到j == 0 :f[i-1][0]-->f[i][0+weight[i]]... -->f[n]/[packageWeight]即只要背包恰好能装满的,都是从f[i][0] 开始,最终能迭代到 f[n][packageWeight] 所以 f[i][0] 都初始化成0。
2)不能装满背包的,背包还有剩空间,问题分解出的子问题最终分解到 j != 0 f[i-1][j!=0]-->f[i-1][j+weight[i]]...-->f[n][packageWeight] 。(最终肯定有f[0][j!=0])
如果要求最终恰好装满背包,则对2)这类分解成的子问题全部排除在外。由于状态方程中使用max比较,为了让能分解到 j == 0 的子问题胜出, 所以对于分解到 j != 0 的这些子问题的初始值,初始化为一个非常小的值(程序中的价值都是大于0 的),如负无穷。
最后算法执行完返回前判断:
(1)f[n][packageWeight] < 0 表示这些物品组合不能刚好装满背包。
(2)否则,能刚好装满背包,返回 f[n][packageWeight]。
用没有优化前的代码做说明:
public int bottomUpZeroOnePackage(int[] weight,int[] value,int n,int packageWeight) {
// 初始化成0 如果初始化成-1时packageWeight=0会得到-1的解
int[][] m_memo = new int[n + 1][packageWeight + 1];
for (int i = 0; i <= n; i++) {
m_memo[i][0] = 0;
}
// 初始化一个最小负值,确保这个负值能够
for (int j = 1; j <= packageWeight; j++) {
m_memo[0][j] = -999999999;
}
for (int i = 1; i<=n; i++) {
// 或者for(int j = packageWeight; j >= 1; j--) 内层循环从大到小循环也可以
for (int j = 1; j <= packageWeight; j++) {
m_memo[i][j] = m_memo[i - 1][j];
if (j >= weight[i]) {
m_memo[i][j] = max(m_memo[i - 1][j], value[i] + m_memo[i - 1][j - weight[i]]);
}
}
}
// 装不满背包的比如返回-1
if (m_memo[n][packageWeight] < 0) {
return -1;
}
else {
return m_memo[n][packageWeight];
}
}
【扩展-回溯】
0-1背包问题还有些延伸问题,计算出的背包价值最大值,到底选取了哪些物品,这就涉及到0-1背包最优解回溯。
背包最优解回溯需要使用问题的 子问题的计算结果,所以:
1)对于做了空间优化的0-1背包问题,则无法实现回溯,因为做了空间优化的没有保存子问题的计算结果。
2)没有带备忘录的递归实现,也无法实现回溯,不带备忘录的递归没有保存子问题的计算结果。
回溯逻辑:
- f(i, j) == f(i-1, j) 时,说明没有选择第 i 个物品,则回到 f(i-1, j) ;
- f(i, j) == f(i-1, j-weight(i)) + value(i) 时,说明装了第 i 个物品,该物品是最优解组成的一部分,随后我们得回到装该物品之前,即回到 f(i-1, j-weight(i)) ;
一直遍历到 i == 1 结束为止,会找到被记录的解,注意是找到被记录解,因为 f(n, packageWeight) 的解可能有多个,这些解都满足价值最大。
// 根据保存子问题的求解结果(m_memo)回溯得到最优解,代码片段如下:
int j = packageWeight;
int i = n;
for (; i >= 1; i--) {
// i == 1如果m_memo[i][j] > 0说明第一个物品被选中
if(i == 1) {
if(m_memo[i][j] > 0) {
System.out.println("select:"+i);
}
}
else {
/* 1、从状态方程看m_memo[i][j]要么等于m_memo[i - 1][j]
要么等于m_memo[i-1][j - weight[i]] + value[i]*/
/* 2、m_memo[i][j] > m_memo[i - 1][j] 则表明m_memo[i][j]
等于m_memo[i-1][j - weight[i]] + value[i],即选中物品i加入了背包*/
if (m_memo[i][j] > m_memo[i - 1][j]) {
System.out.println("select:"+i);
j = j - weight[i];
}
}
}
【为何有多个最优解?】:
从上述程序处理过程: m_memo(i, j) = max(m_memo(i-1, j), value(i) + m_memo(i-1, j-weight(i))) ,如果m_memo(i-1, j) == value(i) + m_memo(i-1, j-weight(i)) 这种情况,这两个子问题的解都满足m_memo(i, j)的要求,但是程序只选取了其中一个子问题的解,记录并且继续执行下去,另外的最优解被丢弃,所以后继回溯得到的解也就是我们选中并且记录的那个子问题的解。
如果要求解出所有最优解,需要求解时考虑 m_memo(i-1, j) == value(i) + m_memo(i-1, j-weight(i)) 这种情况并且需要增加额外的空间来存储。
2)完全背包
有N种物品和一个容量为V的背包,每种物品都有无限件可用。第i种物品的价值是value(i),重量/容量是weight(i)。求解将哪些物品装入背包可使这些物品的重量总和不超过背包容量,且价值总和最大。
【完全背包问题分析思路】:
1)首先:完全背包问题中,最优解的结构:物品种类 和 背包容量 是变化量,是否把 物品的取数 也作为变化量?
不用作为单独的变化量,因为每种物品取几件不确定,所以物品数量的变化可作为物品种类的子问题。
我们假设最优解使用数学函数f(i, j)表示,其含义就是前i种物品装入容量为j的背包总价值最大值,其中变量i和j的取值范围:0<=i<=N(物品种类),0<=j<=V(背包容量)。
2)其次:对f(i, j)问题进行子问题分解:即f(i, j)他是怎么来的:由前i-1种类物品已处理装入背包和对当前种类物品i的选择而来:
(1)子问题1:如果当前种类物品i不装入背包,由f(i, j)逆推子问题1:f(i-1, j),不装入背包的理由可能是j的空间装不下i,也可能是能装的下,但是如果选择装入后的值不一定最优(在众子问题中不是最优的那个)。
(2)子问题2:如果当前种类物品i取1件装入背包,由f(i, j)逆推子问题2:f(i-1, j-weight(i))。
(3)子问题3:如果当前种类物品i取2件装入背包,由f(i, j)逆推子问题3:f(i-1, j-2*weight(i))。
......
循环条件是j-kweight(i)>=0
把上述子问题综合一下: f(i,j)=max{f(i-1,j-kweight(i))+kvalue(i)|0<=kweight(i)<=j},所以有:
- f(i,0) = f(0,j) = 0 条件: i = 0 或 j = 0 ,即背包容量是0或没有物品放入则最大价值是0。
- f(i,j) = f(i-1,j) , j < weight(i) ,背包剩余容量 j 小于第 i 种类物品的容量,第 i 种类物品无法装入背包。
- f(i,j) = f(i-1,j-kweight(i)) + kvalue(i)) , i > 0,j >= kweight(i),k >= 0
或写成这样: f(i,j) = max(f(i-1,j), f(i-1,j-kweight(i)) + kvalue(i)) , i > 0,j >= kweight(i),k>=1 ,背包剩余容量j大于物品种类i的容量,满足装入条件但是:可以不选、也可以选择几个装入。f(i-1, j) 大则表示第i种类物品满足装入条件但是没有装入背包;如果 f(i-1,j-kweight(i)) + kvalue(i) 大则表示第 i 种类物品被选中了k件装入了背包。
代码参考:
......
for (int i = 1; i<=n; i++) {
// 或者for(int j = packageWeight;j>=1;j--) 内层循环从大到小循环也可以
for (int j = 1; j <= packageWeight; j++) {
m_memo[i][j] = m_memo[i - 1][j];
if (j >= weight[i]){
// 加 k*weight[i] !=0防止出现weight[i] == 0出现死循环
for (int k = 1; j >= k * weight[i] && k * weight[i] != 0; k++){
m_memo[i][j] = max(m_memo[i][j], k*value[i] + m_memo[i - 1][j - k * weight[i]]);
}
}
}
}
return m_memo[n][packageWeight];
......
3)多重背包
多重背包: 有N种物品和一个容量为V的背包,每种物品都有 有限个 可选择。第i种物品的价值是value[i],重量/容量是 weight[i],可选数量m[i]。
求解将哪些物品装入背包可使这些物品的重量总和不超过背包容量,且价值总和最大。
分析思路如完全背包。
f(i,j)=max{ f( i-1, j-k*weight[i] ) + k*value[i] |0<=k<=m[i] 且0<= k*weight[i] <=j }
和完全背包相比,k取值多了一个0<=k<=m[i]限制。程序段以及最优解回溯大家自行实现。 关于背包问题还有许多扩展问题,如混合背包,二维费用背包等等请大家自行了解。
4)凑零钱问题
凑零钱问题:有K种面值零钱,c[1],c[2],...c[k],各种面值零钱数量不限,给定一个总金额为M。问最少要多少张这些面值零钱能凑齐总额为M的金额?如果这些面值的零钱中没有可以组合成M的返回-1。
分析如下:
- 首先:最优解的结构:零钱面值,总金额M。用函数f(i,j)来表述所需零钱的张数最小,0<=i<=K,0<=j<=M。
- 其次:f(i, j)的子问题可分解为:
- 子问题1:如果面值i的零钱不选,由f(i, j)逆推子问题1:f(i-1, j)。
- 子问题2:如果面值i的零钱取1张,由f(i, j)逆推子问题2:f(i-1, j-c[i])。
- 子问题3:如果面值i的零钱取2张,由f(i, j)逆推子问题3:f(i-1, j-2 * c[i])。
...... 循环条件是j-k*c[i]>=0。 综合一下: f(i,j) = min
再次:处理一下边界问题:金额为0的f(i,0) = 0 所以有:
1) f[i][0] = 0 条件: j = 0 ,金额为0是表示0张。
2) f[i][j] = f[i-1][j] j < c[i] 如果j小于c[i]面值,则不能选择。
3) f[i][j] = min(f[i-1][j], f[i-1][j-k*c[i]] + k) i > 0 j >= k*c[i] && k*c[i] != 0 k>=1
这
这里还有一个隐含问题,凑零钱必须正好凑齐M,否则k种面值无法组成M金额,这里就涉及到m_memo值初始化问题,恰好凑齐M,所以由前边背包问题中,问题和子问题求解结果保存空间值初始化已做了分析。
代码参考:
int coinChange(int[] coins, int amount) {
if (amount < 0) {
return -1;
}
// m_memo[i][0]初始化成0
int[][] m_memo = new int[coins.length][amount + 1];
for (int i = 0; i < coins.length; i++) {
m_memo[i][0] = 0;
}
// 初始值初始化为 amount + 1
// 主要因为求最小值,所以把问题和子问题的解初始化成amount + 1,因为面值最小单位都是1
// 所以amount大小需要的面值张数不会超过amount
for (int j = 1; j <= amount; j++) {
m_memo[0][j] = amount + 1; //表示还有余额度,作为大值用于后续判断
}
for (int i = 1; i< coins.size(); i++) {
for (int j = 1; j <= amount; j++) {
// j<coins[i]不拿该硬币
m_memo[i][j] = m_memo[i - 1][j];
// j>=coins[i]拿该硬币,拿几个
// m_memo[i - 1][j]也是子问题所以参与min比较,min中m_memo[i][j]初值为m_memo[i - 1][j]
// 相当于满足拿的条件,但是拿还是不拿该面值币看是否满足子问题中最小
if (j >= coins[i]) {
// 所有子问题中取最小, k*coins[i] != 0防止有面值是0出现死循环
for (int k = 1; j >= k * coins[i] && k * coins[i] != 0; k++) {
m_memo[i][j] = min(m_memo[i][j], k + m_memo[i - 1][j - k * coins[i]]);
}
}
}
}
// 计算出结果如果大于amount表明没有这种组合
if (m_memo[coins.length-1][amount] > amount) {
return -1;
}
else {
return m_memo[coins.length-1][amount];
}
}
5)打家劫舍(力扣)(动态规划解法)
有一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈,这意味着第一个房屋和最后一个房屋是紧挨着的。
同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
【分析思路】:
假设i个房间,其内的金钱为money[i]。
则可偷到的最多钱f(i):
1)可能1:i房间不偷,i-1家偷的最多。
2)可能2:i房间偷,i-1家不偷,值最大。
此题是 198. 打家劫舍 的拓展版:唯一的区别是此题中的房间是环状排列的(即首尾相接),而 198.198. 题中的房间是单排排列的;而这也是此题的难点。环状排列意味着第一个房子和最后一个房子中只能选择一个偷窃,因此可以把此环状排列房间 问题约化为两个 单排排列房间 子问题:
- 在不偷窃第一个房子的情况下(即 nums[1:]),最大金额是 p_1p
- 窃最后一个房子的情况下(即 nums[:n-1]),最大金额是 p_2p
所以,可以把原始队列分成两个队列[0][n-1]、[1][n] (房子index是0~n)
为了提醒效率,使用cache。
代码参考:
public int rob(int[] nums) {
int[] cache1 = new int[nums.length];
Arrays.fill(cache1, -1);
if(nums.length >= 2 ) {
int[] nums1 = new int[nums.length - 1];
int[] nums2 = new int[nums.length - 1];
int[] cache2 = new int[nums.length];
Arrays.fill(cache2, -1);
System.arraycopy(nums, 0, nums1, 0, nums.length - 1);
System.arraycopy(nums, 1, nums2, 0, nums.length - 1);
return Math.max(max(nums1, nums1.length - 1, cache1), max(nums2, nums2.length - 1, cache2));
}
else{
return max(nums, nums.length - 1, cache1);
}
}
public int max(int[] nums, int i, int[] cache) {
if(i < 0){
return 0;
}
if(i == 0) {
return nums[i];
}
if(cache[i] != -1) {
return cache[i];
}
int maxNum = Math.max(max(nums, i - 1, cache), nums[i] + max(nums, i-2, cache));
cache[i] = maxNum;
return maxNum;
}
6)分割数组以得到最大和
给出整数数组 A,将该数组分隔为长度最多为 K 的几个(连续) 子数组。 分隔完成后,每个子数组的中的值都会变为该 子数组中的 最大值。
返回给定数组完成分隔后的最大和。
示例:
输入:A = [1,15,7,9,2,5,10], K = 3
输出:84
解释:A 变为 [15,15,15, 9, 10,10,10]
提示:
1 <= K <= A.length <= 500
0 <= A[i] <= 10^6
【解题思路】:

代码参考:
class Solution {
int[] cacheArray = null;
public int maxSumAfterPartitioning(int[] arr, int k) {
cacheArray = new int[arr.length];
Arrays.fill(cacheArray, -1);
return maxSumN(arr, arr.length-1, k);
}
public int maxSumN(int[] A, int index, int K) {
if (index < 0) {
return 0;
}
if (cacheArray[index] != -1) {
return cacheArray[index];
}
int maxNode = 0;
int maxSum = 0;
int left = index, right = index;
// 分割1个元素,计算剩余序列最大值.....分割k个元素,计算剩余序列最大值。
for (; right - left <= K - 1 && left >=0 ; left--) {
// 获取left和right间之间的最大数
for (int m = right; m >= left; m--) {
maxNode = Math.max(maxNode, A[m]);
}
maxSum = Math.max(maxSum, maxSumN(A, left - 1 , K) + (right - left + 1) * maxNode);
}
cacheArray[index] = maxSum;
return maxSum;
}
}
7)分割等和子集(力扣)
给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
注意:
- 每个数组中的元素不会超过 100
- 数组的大小不会超过 200
示例 1:
输入: [1, 5, 11, 5]
输出: true
解释: 数组可以分割成 [1, 5, 5] 和 [11].
示例 2:
输入: [1, 2, 3, 5]
输出: false
解释: 数组不能分割成两个元素和相等的子集.
【思路】:
架设序列和为SUM,本题目本质上是求是否存在子序列、其和=SUM/2
- 求f(n, SUM/2)
- 第n个元素不选择,求f(n - 1, Sum/2); 第n个元素选择,则求f(n-1, SUM/2 - List[n])。 汇总公式为:f(n, SUM/2) = f(n - 1, Sum/2) || f(n-1, SUM/2 - list[n]);
- 采用cache作为缓存。其中:f(n,0) = true;f(0, x) = false (x != 0 && x != List[0])(剩余有值,表示没有刚好=SUM/2)
8)买卖股票的最佳时机
8.1)只买卖一次,求最大利润(非动态规划,但目的和8..4作为一类问题放在一起)
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的 最大利润。你最多可以完成 一笔 交易。
【思路】:
代码参考:
public int maxProfit(int[] prices) {
int maxProfit = 0;
int minPrice = Integer.MAX_VALUE;
for(int i = 0; i < prices.length; i++) {
// 找到已遍历天数的最低价
minPrice = Math.min(minPrice, prices[i]);
// 已遍历天数最低价,和当天价值的价差即为当天卖出的最大利润。计算所有天数作为卖出天的可能最大利润。
maxProfit = Math.max(maxProfit, prices[i] - minPrice);
}
return maxProfit;
}
8.2)不限买卖次数,求最大利润(非动态规划,采用差分。但目的和8..4作为一类问题放在一起)
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的 最大利润。不限制交易笔数。
【思路】:什么时候会有利润,即:比前一天涨价。So,获取当天和前一天的价差(差分),所有涨价天均交易,相当于获得所有价差
代码参考:
public int maxProfit(int[] prices) {
int maxProfit = 0;
for(int i = 1; i < prices.length; i++) {
int tempPriceBalance = prices[i] - prices[i - 1];
if (tempPriceBalance > 0) {
maxProfit += tempPriceBalance;
}
}
return maxProfit;
}
8.3)类似的一个库存问题,包含库存租金支出(非动态规划,采用差分。但目的和8..4作为一类问题放在一起)
将该商品在连续的K天内的价格记录在了数组price中 。在某天(设为i)决定购入某商品,将它们存入仓库。并在另外一天(设为j),将商品卖出(i <= j),同时他还需要付给该仓库j - i元的租金(每天租金为1)。
设计一个算法来计算你所能获取的 最大利润。为了简化实现,整个过程只买卖一次。
输入:price = [2,1,5]
输出:3
解释:最优策略是第二天买入,第三天卖出,租金为1,利润为5 - 1 - 1 = 3
输入:price = [7,6,5]
输出:0
解释:最优策略是任意一天买入,当天卖出,利润为0
限制:
• 1 <= K <= 50000
• 1 <= price[i] <= 300
注:请考虑程序的性能。
【解法一】:采用滑窗暴力解法。注意滑窗最大长度是300,否则 租金 > 价格,肯定无利可图。
【解法二】:
public int transaction(int[] price) {
int maxProfit = 0;
int minCost = price[0]; //以首日买入价格作为初始成本
for (int i = 1; i < price.length; i++) {
// minCost刷新后,通过+1累加minCost成本
minCost = Math.min(price[i], minCost + 1);
maxProfit = Math.max(maxProfit, price[i] - minCost);
}
return maxProfit;
}
8.4)两次交易(困难)
(困难)(力扣)
https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iii/
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的 最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
限制:(遇到这种大范围的限制,就要考虑for循环超时、内存超限、递归栈慢等问题)

方法一:暴力解法
找到一个中间的点,把序列分成2部分。即在每个子序列中交易一次,求两次交易的最大值:
- 第一个序列的终点、第二个序列的起点重合。如:同一天先卖、再买的场景。
- 第一个序列可以是长度可以是0,此时就表示就交易一次。
代码参考如下。(提示超时)
class solution {
public int maxProfit(int[] prices) {
int maxProfit = 0;
for(int mid = 0; mid < prices.length; mid++) {
maxProfit = Math.max(maxProfit, getMaxprofit(prices, 0, mid) + getMaxprofit(prices, mid, prices.length-1));
}
return maxProfit;
}
public int getMaxprofit(int[] prices, int start, int end) {
int maxProfit = 0;
for(int i = start; i < end; i++){
for(int j = i + 1; j <= end; j++) {
maxProfit = Math.max(maxProfit, prices[j] - prices[i]);
}
}
return maxProfit;
}
}
优化:通过[i]/[j]二维数字记录之间最大元素。(提示内存超限制)
class Solution {
//定义一个[n][n]数组,其中[i][j]之间的最大值
int[][] max = null;
public int maxProfit(int[] prices) {
max = new int[prices.length][prices.length];
for(int i = 0; i < prices.length; i++){
int tmpMax = 0;
// 以i为起点,找其后i-j区间内最高价格
for(int j = i; j < prices.length; j++) {
tmpMax = Math.max(tmpMax, prices[j]);
max[i][j] = tmpMax;
}
}
int maxProfit = 0;
for(int mid = 0; mid < prices.length; mid++) {
maxProfit = Math.max(maxProfit, getMaxprofit(prices, 0, mid) + getMaxprofit(prices, mid, prices.length-1));
}
return maxProfit;
}
public int getMaxprofit(int[] prices, int start, int end) {
int maxProfit = 0;
for(int i = start; i <= end; i++){
//直接取i之后最大值-i。
maxProfit = Math.max(maxProfit, max[i][end] - prices[i]);
}
return maxProfit;
}
}
方法一:动态规划(力扣)(困难??)
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
int buy1 = -prices[0], sell1 = 0;
int buy2 = -prices[0], sell2 = 0;
for (int i = 1; i < n; ++i) {
buy1 = Math.max(buy1, -prices[i]);
sell1 = Math.max(sell1, buy1 + prices[i]);
buy2 = Math.max(buy2, sell1 - prices[i]);
sell2 = Math.max(sell2, buy2 + prices[i]);
}
return sell2;
}
}
9)不同路径
【题目】:
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
【分析】:
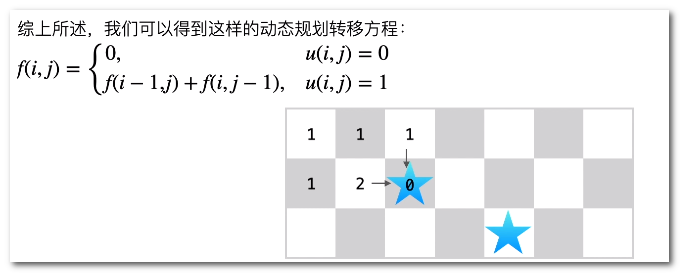
如上分析中:u(i , j)=0,表示位置是石头。
【代码参考】:
自己写的易于理解的:
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int rowNum = obstacleGrid.length, colNum = obstacleGrid[0].length;
int[][] f = new int[rowNum][colNum];
f[0][0] = obstacleGrid[0][0] == 1? 0 : 1;
for (int i = 0; i < rowNum; ++i) {
for (int j = 0; j < colNum; ++j) {
if(i == 0 && j > 0)
f[i][j] = obstacleGrid[i][j] == 1? 0:f[i][j-1];
if(i > 0 && j == 0)
f[i][j] = obstacleGrid[i][j] == 1? 0:f[i-1][j];
if(i>0 && j>0)
f[i][j] = obstacleGrid[i][j] == 1? 0:f[i-1][j] + f[i][j-1];
}
}
return f[rowNum -1][colNum -1];
}
}
力扣内存优化的:
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int rowNum = obstacleGrid.length;
int colNum = obstacleGrid[0].length;
int[] f = new int[colNum];
f[0] = obstacleGrid[0][0] == 0 ? 1 : 0;
for (int i = 0; i < rowNum; ++i) {
for (int j = 0; j < colNum; ++j) {
if (obstacleGrid[i][j] == 1) {
f[j] = 0;
continue;
}
if (j - 1 >= 0 && obstacleGrid[i][j - 1] == 0) {
f[j] += f[j - 1];
}
}
}
return f[m - 1];
}
}
10)串联字符串最大长度
力扣:https://leetcode-cn.com/problems/maximum-length-of-a-concatenated-string-with-unique-characters/
给定一个字符串数组 arr,字符串 s 是将 arr 某一子序列字符串连接所得的字符串,如果 s 中的每一个字符都只出现过一次,那么它就是一个可行解。
请返回所有可行解 s 中最长长度。
示例 1:
输入:arr = ["un","iq","ue"]
输出:4
解释:所有可能的串联组合是 "","un","iq","ue","uniq" 和 "ique",最大长度为 4。
示例 2:
输入:arr = ["cha","r","act","ers"]
输出:6
解释:可能的解答有 "chaers" 和 "acters"。
示例 3:
输入:arr = ["abcdefghijklmnopqrstuvwxyz"]
输出:26
提示:
1 <= arr.length <= 16
1 <= arr[i].length <= 26
arr[i] 中只含有小写英文字母
【思路】:
地域字符集中第i个元素:
1)拼接字符串选择第i个元素,求i+1后的子序列的最大长度。(求i+1后的子序列的最大长度,需要排除掉包含第i元素中字符的元素)
2)拼接字符串不选择第i个元素,求i+1后的子序列的最大长度。
So,两个关键元素:i--字符串序列中起始字符串Index;exceptSet--记录需要排除的字符(即已拼接元素包含的字符)
换算公式即:f(i, exception) = Max((1), (2))
- (1)不使用当前字符串:f(i+1, exception)
- (2)使用当前字符串串:f(i+1, exception.add(dictionary[i])) + dictionary[i].length)
代码参考:
public int maxLength(List<String> arr) {
Set<Character> exception = new HashSet<>();
/* 递归是相关元素: f(i, exception) = Max((1), (2)) --i:字典下标,exception:已使用过的字符
* (1)不使用当前字符串:f(i+1, exception)
* (2)使用当前字符串串:f(i+1, exception.add(dictionary[i])) + dictionary[i].length)
*
备忘录:下标索引对应dictionary的索引,值为是Set(exception)
*/
Map<Pair<Integer, Set<Character>>, Integer> cache = new HashMap<>();
return dfsLen(arr, 0, 0, exception, cache);
}
public int dfsLen(List<String> arr, int index, int len, Set<Character> exception,
Map<Pair<Integer, Set<Character>>, Integer> cache) {
if (index == arr.size()) {
return len;
}
Pair<Integer, Set<Character>> key = new Pair<>(index, exception);
if (cache.containsKey(key)) {
return cache.get(key);
}
int len1 = dfsLen(arr, index + 1, len, exception, cache);
int len2 = 0;
if (strCanbeUsed(arr.get(index), exception)) {
// 使用临时Set结构,为了递归返回后方便还原现场
Set<Character> tmpException = new HashSet<>(exception);
addStr2Exception(arr.get(index), tmpException);
len2 = dfsLen(arr, index + 1, len + arr.get(index).length(), tmpException, cache);
}
int retLen = Math.max(len1, len2);
cache.put(key, retLen);
return retLen;
}
public boolean strCanbeUsed(String str, Set<Character> exception) {
Set<Character> charSet = new HashSet<>();
for (int i = 0; i < str.length(); i++) {
// 字符串是否包含被排除字符
if (exception.contains(str.charAt(i))) {
return false;
}
// 字符串自身是否包含重复字符
if (charSet.contains(str.charAt(i))) {
return false;
} else {
charSet.add(str.charAt(i));
}
}
return true;
}
public void addStr2Exception(String str, Set<Character> exception) {
for (int i = 0; i < str.length(); i++) {
if (!exception.contains(str.charAt(i))) {
exception.add(str.charAt(i));
}
}
return;
}
11)四键键盘(困难 ??)
https://www.cnblogs.com/labuladong/p/12320268.html
12)轰炸敌人
https://blog.csdn.net/qq_43765535/article/details/111084182
【解题思路一】:炸弹位置是四个方向前缀和之和。
【解题思路二】:Up[i]/[j]表示[i]/[j]位置炸弹,能向上炸死最多人数;Down[i]/[j]表示[i]/[j]位置炸弹,能向上炸死最多人数;Left[i]/[j]表示[i]/[j]位置炸弹,能向上炸死最多人数;right[i]/[j]表示[i]/[j]位置炸弹,能向上炸死最多人数;四个方向分别DP。
13)校园自行车分配(??)
参考:https://blog.csdn.net/malimingwq/article/details/89365249
按照:这个题我们首先得到所有的(工人索引,自行车索引,曼哈顿距离)作为存储对象,然后以曼哈顿距离为主,工人索引次之,自行车索引方式再次之的方式将这些对象按升序排列,最后按顺序遍历三元组给工人分配自行车即可。
14)抛掷硬币
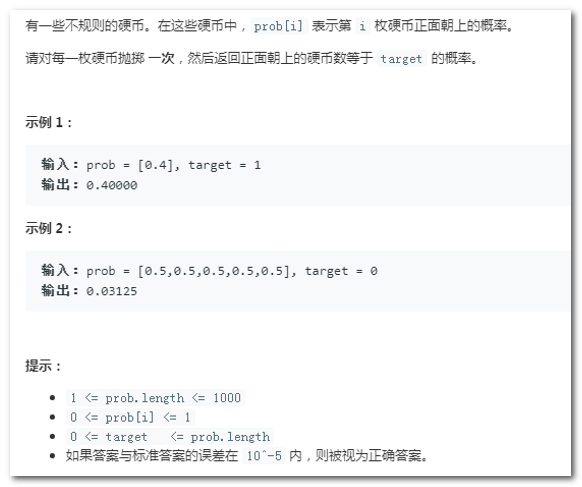
此题用动态规划,状态方程:
arr[i][0] = arr[i-1][0] * (1-prob[i])
arr[i][j] = arr[i-1][j] * (1-prob[i]) + dp[i-1]/[j-1] * prob[i] (target=>j>0)
arr[i][0]代表抛掷第i枚硬币中出现0次正面的次数
arr[i][j]代表抛掷第i枚硬币中出现j次正面的次数




