【算法】广度优先算法BFS
一、算法理解
广度优先搜索算法(Breadth-First-Search,BFS),又称宽度优先搜索。作为最简便的图的搜索算法之一,是很多重要图算法的基本原型,如Dijkstra最短路径算法和Prime最小生成树算法。其核心思想是:
- 从初始节点开始,应 用产生式规则生成第一层节点,检查目标节点是否在这些后继节点中。
- 若没有,则再用产生式规则将第一层所有节点逐一扩展,得到第二层节点,并逐一检查第二层节点中是否包含目标节点。
- 若没有,则继续扩展第二层的节点。
- 如此类推,直至发现目标节点为止。
广度优先搜索是一种分层的查找过程,每向前走一步可能访问一批顶点,不像深度优先搜索那样有往回退的情况,因此它不是一个递归的算法。为了实现逐层的访问,算法必须借助一个辅助队列,以记录正在访问的顶点的下一层 顶点。
【样例便于理解】:
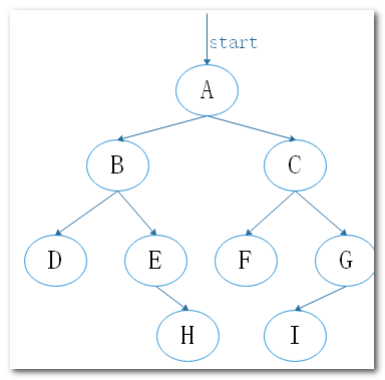
- 首先从顶点A开始,将 A 入队列Queue , visited[A]=true ,表示顶点A已被访问;
- 此时队列 Queue 非空,取出队头元素A,将其相邻的未被访问的顶点(B,C)依次访问,并插入队列 Queue ;
- 队列非空,取出队头元素B,将其将其相邻的未被访问的顶点(D,E)依次访问,并插入队列 Queue ;
- 队列非空,取出队头元素C,将其将其相邻的未被访问的顶点(F,G)依次访问,并插入队列 Queue ;
- 取出队头元素D,无相邻未被访问顶点;
- 取出队头元素E,将其将其相邻的未被访问的顶点(H)依次访问,并插入队列 Queue ;
- 取出队头元素F,无相邻未被访问顶点;
- 取出队头元素G,将其将其相邻的未被访问的顶点(I)依次访问,并插入队列 Queue ;
- 取出队头元素H,无相邻未被访问顶点;
- 取出队头元素I,无相邻未被访问顶点;
- 队列为空,循环跳出,遍历结果为: A->B->C->D->E->F->G->H->I ;
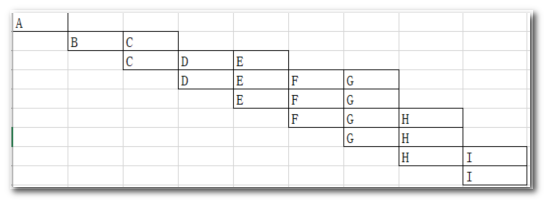
伪码参考:
void BFS() {
1. 初始化:遍历需要的队列Q、标志节点是否访问过visited
2. 起始节点入队列:Q.push(startNode)
3. 标志起始节点已经在队列当中了: visited[startNode] = true
while (!Q.empty()) {//队列非空
node = Q.poll() //需要遍历的节点出队列
nearList = getNearList(node) //获取node节点的邻接节点集合
for (nearNode : nearList) { //对每一个邻接点,执行
if (visited[nearNode] != true) {//如果邻接点没有被访问
Q.add(nearNode) //把邻接点加入队列,等待访问
visited[nearNode] = true //标志邻接点已经在队列当中了:
二、适用场景
广度优先搜索算法可以用来解决两类问题:
- 从节点A出发,有前往节点B的路径吗?(迷宫问题)
- 从节点A出发,前往节点B的哪条路径 最短?(最短路径问题)
三、注意事项
【核心数据结构】:
- 一个数据结构记录无向图(主要图中连线关系)。
- 一个数据结构记录节点 是否被访问过 避免重复访问)。
- 一个 先进先出队列,记录遍历过程。如果需要返回深度,队列每个元素同时 节点 在无向图中层级。
四、使用案例
1)单词接龙☆☆☆
字典 wordList 中从单词 beginWord 和 endWord 的转换序列是一个按下述规格形成的序列:
- 序列中第一个单词是 beginWord 。
- 序列中最后一个单词是 endWord 。
- 每次转换只能改变一个字母。
- 转换过程中的中间单词必须是字典 wordList 中的单词。
给你两个单词 beginWord 和 endWord 和一个字典 wordList ,找到从 beginWord 到 endWord的最短转换序列中的单词数目 。如果不存在这样的转换序列,返回 0。
示例 1:
输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出:5
解释:一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。
示例 2:
输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
输出:0
解释:endWord "cog" 不在字典中,所以无法进行转换。
提示:
1 <= beginWord.length <= 10
endWord.length == beginWord.length
1 <= wordList.length <= 5000
wordList[i].length == beginWord.length
beginWord、endWord 和 wordList[i] 由小写英文字母组成
beginWord != endWord
wordList 中的所有字符串 互不相同
【问题分析】:
根据题目意思,我们可以抽象地认为这是一个图的最短路径问题,初始节点为 beginWord ,目标节点为 endWord ,
中间节点为 wordList 给定的单词,现在我们已经明确了开始节点和目标节点,但是中间节点的邻接关系我们还没有确定,根据题目中每次转换只能改变一个字母这一条件,明确只有一个字母差距的单词可以连上一条边,构成邻接关系。因此,可以将示例1的输入构成构成一个无向图,如下(图片来源LeetCode):
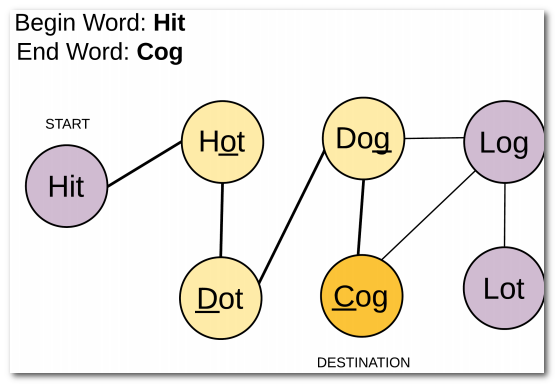
至此,题目变成了一个寻找目标节点的最短路径问题,因此可以使用 “广度优先算法” 求解。
这道题的重点在于如何建立邻接关系,根据每次转换只能改变一个字母,可以先对wordList中的单词进行预处
理,将单词中的某个字母用"_"替换,这个预处理可以帮助我们构造一个单词变换的通用状态,例如: Hit->H_t<-
Hot 。
问题实现:
- 对给定的 wordList 做预处理,找出所有的通用状态。将通用状态记录在字典中,键是通用状态,值是所有
具有通用状态的单词; - 将包含 (beginWord, 1) 的元组放入队列中,beginWord 为初始节点,1表示初始节点的层数。我们需要返
回 endWord 的层次也就是从 beginWord 出发的最短距离;
数据结构:
- 定义HashMap<String, ArrayList
>,记录节点之间无向树关系。
注意:对于hot,来说,满足_ot、h_t、ho_都是其相邻节点。为了后续检索效率,分别作为不同的key,保存如HashMap。 - 定义ArrayQueue<Pair<String, Integer>>记录节点遍历队列。String记录节点值,Integer记录节点所在层级。
- 定义HashSet
记录节点是否已遍历过,String记录节点值,
样例代码:
public static int ladderLength(String beginWord, String endWord, List<String> wordList) {
//wordList转换成记录的无向树
HashMap<String, ArrayList<String>> tree = new HashMap<String, ArrayList<String>>();
for(int i = 0; i < wordList.size(); i++) {
String word = wordList.get(i);
int length = word.length();
for (int j = 0; j < length; j++) {
String tmpStr = word.substring(0,j) + "_" + word.substring(j + 1, length);
if(!tree.containsKey(tmpStr)) {
tree.put(tmpStr, new ArrayList<String>(Collections.singletonList(word)));
}
else {
tree.get(tmpStr).add(word);
}
}
}
//创建遍历队列:
ArrayDeque<Pair<String,Integer>> queue = new ArrayDeque<Pair<String,Integer>>();
HashSet<String> tags = new HashSet<String>();
queue.addLast(new Pair<>(beginWord, 1));
tags.add(beginWord);
while(!queue.isEmpty()) {
Pair<String, Integer> tmpPair = queue.pollFirst();
String tmpWord = tmpPair.getKey();
if (tmpWord.equals(endWord)) {
return tmpPair.getValue();
}
for (int k = 0; k < tmpWord.length(); k++) {
String tmpStr2 = tmpWord.substring(0, k) + "_" + tmpWord.substring(k + 1, tmpWord.length());
ArrayList<String> tmpList = tree.get(tmpStr2);
if (tmpList != null) {
for (String str : tmpList) {
if (str.equals(endWord)) {
return tmpPair.getValue() + 1;
} else if (!tags.contains(str)) {
queue.addLast(new Pair(str, tmpPair.getValue() + 1));
tags.add(str);
}
}
}
}
}
return 0;
}
2)被围绕的区域
https://leetcode-cn.com/problems/surrounded-regions
给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' ,找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
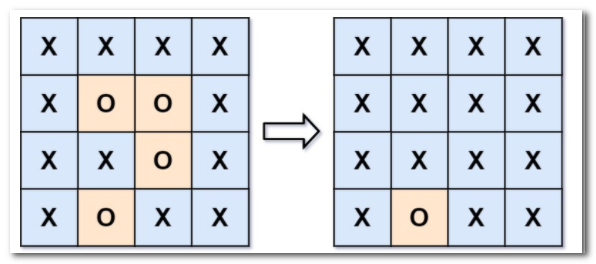
示例 1:
输入:board = [
["X","X","X","X"],
["X","O","O","X"],
["X","X","O","X"],
["X","O","X","X"]]
输出:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释:被围绕的区间不会存在于边界上,换句话说,任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上,或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
示例 2:
输入:board = [["X"]]
输出:[["X"]]
提示:
m == board.length
n == board[i].length
1 <= m, n <= 200
board[i]/[j] 为 'X' 或 'O'
【思路分析】--暴力解发:
- 遍历二维数组中元素,如果是0,则以其为启动,向上下左右找1,直到最终所有方向都找到1,则刷新为。(并不行,每个0都需要上下左右)
- 基础处理下一元素。
【思路分析】:
把0节点按照上下左右组成树关系,如果最终所有叶子节点都是1,则说明是合围的。(边缘节点章节算叶子节点)

- DFS优先检索的,就是上下左右。
- 为了加快消息,增加一个序列。记录DFS过程中遇到的0位置,如果树中所有0是合围的,所有0节点全部置为1节点。
代码参考:
public static void solve(char[][] board) {
if(board.length == 0 || board[0].length == 0) {
return;
}
for(int i = 0; i<board.length; i++) {
for(int j=0; j <board[0].length; j++) {
if(board[i][j] == 'O') {
judgeNodeIsTrue(board, i, j);
}
}
}
}
public static void judgeNodeIsTrue(char[][] board, int rowIndex, int colIndex) {
//定义队列
ArrayDeque<Pair<Integer, Integer>> queue = new ArrayDeque<Pair<Integer, Integer>>();
//定义标志数组,找过的,不需要重复找。避免两个相邻的0节点互相找
HashSet<Pair<Integer, Integer>> flags = new HashSet<Pair<Integer, Integer>>();
//记录过程中遇到的0节点
ArrayDeque<Pair<Integer, Integer>> zeroNodes = new ArrayDeque<Pair<Integer, Integer>>();
int[][] direct = new int[][]{{0, -1}, {0 ,1}, {-1, 0}, {1, 0}};
queue.addLast(new Pair<>(rowIndex, colIndex));
flags.add(new Pair<>(rowIndex, colIndex));
zeroNodes.addLast(new Pair<>(rowIndex, colIndex));
while(!queue.isEmpty()) {
Pair<Integer, Integer> node = queue.pollFirst();
int row = node.getKey();
int col = node.getValue();
if(row == 0 || row == board.length - 1 || col == 0 || col == board[0].length - 1) {
return;
}
for(int k = 0; k < direct.length; k++) {
int newRow = row + direct[k][0];
int newCol = col + direct[k][1];
if(board[newRow][newCol]=='O' && !flags.contains(new Pair<>(newRow, newCol))) {
queue.addLast(new Pair<>(newRow, newCol));
flags.add(new Pair<>(newRow, newCol));
zeroNodes.addLast(new Pair<>(newRow, newCol));
}
}
}
while(!zeroNodes.isEmpty()) {
Pair<Integer, Integer> node2 = zeroNodes.pollFirst();
board[node2.getKey()][node2.getValue()] = 'X';
}
return;
}
3)离建筑最近距离

【解题思路】:
可以考虑分别以三个建筑(三个为1的点),分别BFS方式查找到所有空地0的深度。三次BFS后,获得:
- 每个空地 与建筑物 [0,0]、[0, 4]、[2,2]的距离。总中找到到三个建筑物距离和最小的点。
public static int solve(int[][] board) {
if(board.length == 0 || board[0].length == 0) {
return 0;
}
int[][] distForZreo = new int[board.length][board[0].length];
//遍历每个1节点,计算其他0节点到其的距离,距离值累加入distForZreo中保存
for(int i = 0; i<board.length; i++) {
for(int j=0; j <board[0].length; j++) {
if(board[i][j] == 1) {
bfsFineZero(board, i, j, distForZreo);
}
}
}
//遍历distForZreo中记录的所有0节点到三个1节点的累加值,找最小值
int minDistance = Integer.MAX_VALUE;
for(int k = 0; k<board.length; k++) {
for (int l = 0; l < board[0].length; l++) {
if (distForZreo[k][l] != 0) {
minDistance = Math.min(minDistance, distForZreo[k][l]);
}
}
}
return minDistance;
}
public static void bfsFineZero(int[][] board, int rowIndex, int colIndex, int[][] distForZreo) {
//定义queue节点结构,记录为0的二威数组单元所以、及其到根节点1的距离
class queueNode {
int rowIdx;
int colIdx;
int distance;
public queueNode(int row, int col, int distance) {
this.rowIdx = row;
this.colIdx = col;
this.distance = distance;
}
};
//定义队列,需要查找距离,搜易需要记录遍历的节点的深度
ArrayDeque<queueNode> queue = new ArrayDeque<queueNode>();
//定义标志数组,找过的,不需要重复找。避免两个相邻的0节点互相找
HashSet<Pair<Integer, Integer>> flags = new HashSet<Pair<Integer, Integer>>();
//定义数组root关联节点的方向
int[][] direct = new int[][]{{0, -1}, {0 ,1}, {-1, 0}, {1, 0}};
queue.addLast(new queueNode(rowIndex,colIndex,0));
flags.add(new Pair<>(rowIndex, colIndex));
//{1,0,2,0,1},
//{0,0,0,0,0},
//{0,0,1,0,0}
while(!queue.isEmpty()) {
queueNode node = queue.pollFirst();
int row = node.rowIdx;
int col = node.colIdx;
//如果是0节点,保存其到root(1节点)的距离
if(board[row][col] == 0) {
distForZreo[row][col] += node.distance;
}
//遍历4个方向,如果是0节点,则入栈,因为是可达的。1/2接线不可通过,不需再向下找
for(int k = 0; k < direct.length; k++) {
int newRow = row + direct[k][0];
int newCol = col + direct[k][1];
if(newRow >=0 && newRow < board.length && newCol >=0 && newCol < board[0].length
&& board[newRow][newCol] == 0 && !flags.contains(new Pair<>(newRow, newCol))) {
queue.addLast(new queueNode(newRow,newCol,node.distance + 1));
flags.add(new Pair<>(newRow, newCol));
}
}
}
}
4)迷宫(力扣)☆☆☆☆☆
在迷宫中有一个球,里面有空的空间和墙壁。球可以通过滚上,下,左或右移动,
给定球的起始位置,目的地和迷宫,找出让球停到目的地的最短距离。距离为求从起始位置到目标位置经过的空地个数。
迷宫由二维数组表示。1表示墙和0表示空的空间。你可以假设迷宫的边界都是墙。开始和目标坐标用行和列索引表示。
输入:
map =
[
[0,0,1,0,0],
[0,0,0,0,0],
[0,0,0,1,0],
[1,1,0,1,1],
[0,0,0,0,0]
]
start = [0,4]
end = [3,2]
输出:6
【思路分析】:
以起点为根,BFS方式找目标节点:
- 找到,返回前一节点Distance + 1。
- 循环完毕,找不到,返回-1 。
代码参考:
public static int solve(int[][] board, int startRow, int startCol, int endRow, int endCol) {
if(board.length == 0 || board[0].length == 0
|| startRow < 0 || startCol < 0
|| startCol >= board.length || endCol >= board.length) {
return 0;
}
//定义queue节点结构,记录为0的二威数组单元所以、及其到根节点1的距离
class queueNode {
int rowIdx;
int colIdx;
int distance;
public queueNode(int row, int col, int distance) {
this.rowIdx = row;
this.colIdx = col;
this.distance = distance;
}
};
//定义队列,需要查找距离,搜易需要记录遍历的节点的深度
ArrayDeque<queueNode> queue = new ArrayDeque<queueNode>();
//定义标志数组,找过的,不需要重复找。避免两个相邻的0节点互相找
HashSet<Pair<Integer, Integer>> flags = new HashSet<Pair<Integer, Integer>>();
//定义数组root关联节点的方向
int[][] direct = new int[][]{{0, -1}, {0 ,1}, {-1, 0}, {1, 0}};
queue.addLast(new queueNode(startRow,startCol,0));
flags.add(new Pair<>(startRow, startCol));
while(!queue.isEmpty()) {
queueNode node = queue.pollFirst();
int row = node.rowIdx;
int col = node.colIdx;
//遍历4个方向,如果是0节点,则入栈,因为是可达的。1/2接线不可通过,不需再向下找
for(int k = 0; k < direct.length; k++) {
int newRow = row + direct[k][0];
int newCol = col + direct[k][1];
if(newRow >=0 && newRow < board.length && newCol >=0 && newCol < board[0].length) {
if(newRow == endRow && newCol == endCol) {
return node.distance + 1;
}
if(board[newRow][newCol] == 0 && !flags.contains(new Pair<>(newRow, newCol))) {
queue.addLast(new queueNode(newRow, newCol, node.distance + 1));
flags.add(new Pair<>(newRow, newCol));
}
}
}
}
return -1;
}
5)扫雷游戏
让我们一起来玩扫雷游戏!
给定一个代表游戏板的二维字符矩阵。 'M' 代表一个未挖出的地雷,'E' 代表一个未挖出的空方块,'B' 代表没有相邻(上,下,左,右,和所有4个对角线)地雷的已挖出的空白方块,数字('1' 到 '8')表示有多少地雷与这块已挖出的方块相邻,'X' 则表示一个已挖出的地雷。
现在给出在所有未挖出的方块中('M'或者'E')的下一个点击位置(行和列索引),根据以下规则,返回相应位置被点击后对应的面板:
如果一个地雷('M')被挖出,游戏就结束了- 把它改为 'X'。
如果一个没有相邻地雷的空方块('E')被挖出,修改它为('B'),并且所有和其相邻的未挖出方块都应该被递归地揭露。
如果一个至少与一个地雷相邻的空方块('E')被挖出,修改它为数字('1'到'8'),表示相邻地雷的数量。
如果在此次点击中,若无更多方块可被揭露,则返回面板。
示例 1:
输入:
[['E', 'E', 'E', 'E', 'E'],
['E', 'E', 'M', 'E', 'E'],
['E', 'E', 'E', 'E', 'E'],
['E', 'E', 'E', 'E', 'E']]
Click : [3,0]
输出:
[['B', '1', 'E', '1', 'B'],
['B', '1', 'M', '1', 'B'],
['B', '1', '1', '1', 'B'],
['B', 'B', 'B', 'B', 'B']]
示例 2:
输入:
[['B', '1', 'E', '1', 'B'],
['B', '1', 'M', '1', 'B'],
['B', '1', '1', '1', 'B'],
['B', 'B', 'B', 'B', 'B']]
Click : [1,2]
输出:
[['B', '1', 'E', '1', 'B'],
['B', '1', 'X', '1', 'B'],
['B', '1', '1', '1', 'B'],
['B', 'B', 'B', 'B', 'B']]
注意:
输入矩阵的宽和高的范围为 [1,50]。
点击的位置只能是未被挖出的方块 ('M' 或者 'E'),这也意味着面板至少包含一个可点击的方块。
输入面板不会是游戏结束的状态(即有地雷已被挖出)。
简单起见,未提及的规则在这个问题中可被忽略。例如,当游戏结束时你不需要挖出所有地雷,考虑所有你可能赢得游戏或标记方块的情况。
【分析思路】:
- 起始坐标是M,直接设置X,返回。
- 起始坐标不是M,根据指定点BFS递归
- 单开当前节点,遍历周边八个方向节点设置后的值,
- 如果周边全非M,则点开的值为B;B周边节点不可能是炸弹,可以继续加入队列点开。
- 如果周边存在M,则点开的值为炸点数量;炸弹数量周边的节点不知道具体哪个是炸点,不敢点开,不加入队里
- 单开当前节点,遍历周边八个方向节点设置后的值,
public static void solve(char[][] board, int startRow, int startCol) {
if(board.length == 0 || board[0].length == 0
|| startRow < 0 || startRow >= board.length
|| startCol < 0 || startCol >= board[0].length) {
return;
}
if(board[startRow][startCol] == 'M') {
board[startRow][startCol] = 'X';
return;
}
//定义队列,需要查找距离,搜易需要记录遍历的节点的深度
ArrayDeque<Pair<Integer, Integer>> queue = new ArrayDeque<Pair<Integer, Integer>>();
//定义标志数组,找过的,不需要重复找。避免两个相邻的0节点互相找
HashSet<Pair<Integer, Integer>> flags = new HashSet<Pair<Integer, Integer>>();
//定义数组root关联节点的方向
int[][] direct = new int[][]{{0, -1}, {0 ,1}, {-1, 0}, {1, 0}, {-1, -1},{-1, 1} ,{1, -1} ,{1, 1}};
queue.addLast(new Pair<>(startRow,startCol));
flags.add(new Pair<>(startRow, startCol));
while(!queue.isEmpty()) {
Pair node = queue.pollFirst();
int row = (Integer)node.getKey();
int col = (Integer)node.getValue();
HashSet<Pair<Integer,Integer>> tempSet = new HashSet<Pair<Integer,Integer>>();
int minesNum = 0;
//遍历8个方向,如果是0节点,则入栈,因为是可达的。1/2接线不可通过,不需再向下找
for(int k = 0; k < direct.length; k++) {
int newRow = row + direct[k][0];
int newCol = col + direct[k][1];
if(newRow >=0 && newRow < board.length && newCol >=0 && newCol < board[0].length) {
if (board[newRow][newCol] == 'M') {
minesNum++;
break;
}
else if(!flags.contains(new Pair<>(newRow, newCol))) {
tempSet.add(new Pair<>(newRow, newCol));
}
}
}
if(minesNum == 0) {
board[row][col] = 'B';
queue.addAll(tempSet);
flags.addAll (tempSet);
tempSet.clear();
}
else {
board[row][col] = (char) (minesNum + '0');
}
}
return;
}
6)推箱子
「推箱子」是一款风靡全球的益智小游戏,玩家需要将箱子推到仓库中的目标位置。
游戏地图用大小为 n * m 的网格 grid 表示,其中每个元素可以是墙、地板或者是箱子。
现在你将作为玩家参与游戏,按规则将箱子 'B' 移动到目标位置 'T' :
玩家用字符 'S' 表示,只要他在地板上,就可以在网格中向上、下、左、右四个方向移动。
地板用字符 '.' 表示,意味着可以自由行走。
墙用字符 '#' 表示,意味着障碍物,不能通行。
箱子仅有一个,用字符 'B' 表示。相应地,网格上有一个目标位置 'T'。
玩家需要站在箱子旁边,然后沿着箱子的方向进行移动,此时箱子会被移动到相邻的地板单元格。记作一次「推动」。
玩家无法越过箱子。
返回将箱子推到目标位置的最小 推动 次数,如果无法做到,请返回 -1。
示例 1:
输入:grid = [["#","#","#","#","#","#"],
["#","T","#","#","#","#"],
["#",".",".","B",".","#"],
["#",".","#","#",".","#"],
["#",".",".",".","S","#"],
["#","#","#","#","#","#"]]
输出:3
解释:我们只需要返回推箱子的次数。
示例 2:
输入:grid = [["#","#","#","#","#","#"],
["#","T","#","#","#","#"],
["#",".",".","B",".","#"],
["#","#","#","#",".","#"],
["#",".",".",".","S","#"],
["#","#","#","#","#","#"]]
输出:-1
示例 3:
输入:grid = [["#","#","#","#","#","#"],
["#","T",".",".","#","#"],
["#",".","#","B",".","#"],
["#",".",".",".",".","#"],
["#",".",".",".","S","#"],
["#","#","#","#","#","#"]]
输出:5
解释:向下、向左、向左、向上再向上。
示例 4:
输入:grid = [["#","#","#","#","#","#","#"],
["#","S","#",".","B","T","#"],
["#","#","#","#","#","#","#"]]
输出:-1
提示:
1 <= grid.length <= 20
1 <= grid[i].length <= 20
grid 仅包含字符 '.', '#', 'S' , 'T', 以及 'B'。
grid 中 'S', 'B' 和 'T' 各只能出现一个。
【思路】:
- 箱子B能到目标T。
- 人S 能到B的周边位置。
So,两次BFS:
-
第一次BFS,计算人能到的位置全集(包含T、B所在位置),记录下来。
-
第二次BFS,计算B能到F的可行路径:
此时在逐层遍历中,箱子可达下层节点的条件是:
- 目标节点非墙,目标节点的对称节点人能达到。
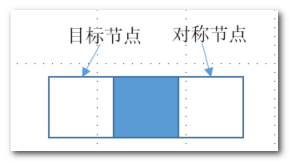
- 为了避免如下情况,判断对称节点可达时:除了判断对称节点在人可达集中外,同时判断外围的三个节点至少一个在人可达集合内。
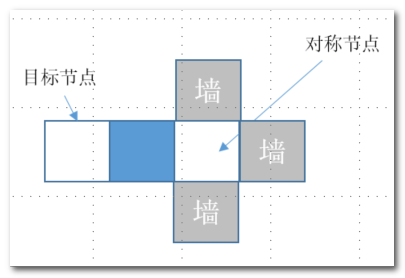
- 目标节点非墙,目标节点的对称节点人能达到。
代码参考:
public static int bfs(char[][] board, int[] box, int[] persion, int[] dest) {
//记录人可达集合
class Node {
int rowIndex;
int colIndex;
int dest;
public Node(int row, int col, int dest) {
this.rowIndex = row;
this.colIndex = col;
this.dest = dest;
}
}
//定义队列,需要查找距离,搜易需要记录遍历的节点的深度
ArrayDeque<Node> queue = new ArrayDeque<Node>();
//定义标志数组,找过的,不需要重复找。避免两个相邻的0节点互相找
HashSet<Pair<Integer, Integer>> arrivedNodes = new HashSet<Pair<Integer, Integer>>();
//定义数组root关联节点的方向
int[][] direct = new int[][]{{0, -1}, {0 ,1}, {-1, 0}, {1, 0}};
queue.addLast(new Node(persion[0], persion[1], 0));
arrivedNodes.add(new Pair<>(persion[0], persion[1]));
while(!queue.isEmpty()) {
Node node = queue.pollFirst();
int row = node.rowIndex;
int col = node.colIndex;
//遍历4个方向,如果是0节点,则入栈,因为是可达的。1/2接线不可通过,不需再向下找
for(int k = 0; k < direct.length; k++) {
int newRow = row + direct[k][0];
int newCol = col + direct[k][1];
if(newRow >=0 && newRow < board.length && newCol >=0 && newCol < board[0].length) {
if ((board[newRow][newCol] == '.' || board[newRow][newCol] == 'T' || board[newRow][newCol] == 'B') && !arrivedNodes.contains(new Pair<>(newRow, newCol))) {
queue.addLast(new Node(newRow, newCol, 0));
arrivedNodes.add(new Pair<>(newRow, newCol));
}
}
}
}
//请空queue,用于下一步记录箱子
queue.clear();
//定义标志数组,找过的,不需要重复找。避免两个相邻的0节点互相找
HashSet<Pair<Integer, Integer>> flags = new HashSet<Pair<Integer, Integer>>();
queue.addLast(new Node(box[0], box[1], 0));
flags.add(new Pair<>(box[0], box[1]));
while(!queue.isEmpty()) {
Node node = queue.pollFirst();
int row1 = node.rowIndex;
int col1 = node.colIndex;
if (row1 == dest[0] && col1 == dest[1]) {
return node.dest;
}
int leftNodeRow = row1;
int leftNodeCol = col1-1;
int rightNodeRow = row1;
int rightNodeCol = col1+1;
int upNodeRow = row1-1;
int upNodeCol = col1;
int downNodeRow = row1+1;
int downNodeCol = col1;
if(arrivedNodes.contains(new Pair<>(leftNodeRow, leftNodeCol)) && arrivedNodes.contains(new Pair<>(rightNodeRow, rightNodeCol))) {
if((arrivedNodes.contains(new Pair<>(leftNodeRow-1, leftNodeCol))
|| arrivedNodes.contains(new Pair<>(leftNodeRow+1, leftNodeCol))
|| arrivedNodes.contains(new Pair<>(leftNodeRow, leftNodeCol-1)))
&& !flags.contains(new Pair<>(rightNodeRow, rightNodeCol))) {
queue.addLast(new Node(rightNodeRow, rightNodeCol, node.dest +1));
flags.add(new Pair<>(rightNodeRow, rightNodeCol));
}
if((arrivedNodes.contains(new Pair<>(rightNodeRow-1, rightNodeCol))
|| arrivedNodes.contains(new Pair<>(rightNodeRow+1, rightNodeCol))
|| arrivedNodes.contains(new Pair<>(rightNodeRow, rightNodeCol+1)))
&& !flags.contains(new Pair<>(leftNodeRow, leftNodeCol))) {
queue.addLast(new Node(leftNodeRow, leftNodeCol, node.dest +1));
flags.add(new Pair<>(leftNodeRow, leftNodeCol));
}
}
if(arrivedNodes.contains(new Pair<>(upNodeRow, upNodeCol)) && arrivedNodes.contains(new Pair<>(downNodeRow, downNodeCol))) {
if((arrivedNodes.contains(new Pair<>(upNodeRow-1, upNodeCol))
|| arrivedNodes.contains(new Pair<>(upNodeRow, upNodeCol-1))
|| arrivedNodes.contains(new Pair<>(upNodeRow, upNodeCol+1)))
&& !flags.contains(new Pair<>(downNodeRow, downNodeCol))) {
queue.addLast(new Node(downNodeRow, downNodeCol, node.dest +1));
flags.add(new Pair<>(downNodeRow, downNodeCol));
}
if((arrivedNodes.contains(new Pair<>(downNodeRow-1, downNodeCol))
|| arrivedNodes.contains(new Pair<>(downNodeRow, downNodeCol-1))
|| arrivedNodes.contains(new Pair<>(downNodeRow, downNodeCol+1)))
&& !flags.contains(new Pair<>(upNodeRow, upNodeCol))) {
queue.addLast(new Node(upNodeRow, upNodeCol, node.dest +1));
flags.add(new Pair<>(upNodeRow, upNodeCol));
}
}
}
return -1;
}
结果,其他都对,如下情况下:
返回了5,预期结果是7:
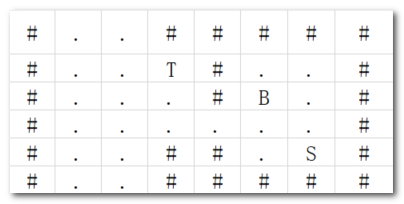
原因是箱子在红点时,人过不去了,要先把箱子推出去。
So,人的可达点是变化的,不能采用如上先遍历所有可达点、缓存的方式。
【优化】:每次根据箱子预期位置,动态计算人是否可达
public static boolean persionArrived(char[][] board, int[]cur, int[] dest) {
//定义队列,需要查找距离,搜易需要记录遍历的节点的深度
ArrayDeque<Pair<Integer, Integer>> queue = new ArrayDeque<Pair<Integer, Integer>>();
//定义标志数组,找过的,不需要重复找。避免两个相邻的0节点互相找
HashSet<Pair<Integer, Integer>> flags = new HashSet<Pair<Integer, Integer>>();
//定义数组root关联节点的方向
int[][] direct = new int[][]{{0, -1}, {0 ,1}, {-1, 0}, {1, 0}};
//Pair tmpPair = new Pair<>(cur[0],cur[1]);
queue.addLast(new Pair<>(cur[0],cur[1]));
flags.add(new Pair<>(cur[0],cur[1]));
while(!queue.isEmpty()) {
Pair node = queue.pollFirst();
int row = (Integer)node.getKey();
int col = (Integer)node.getValue();
if(row == dest[0] && col == dest[1])
{
return true;
}
//遍历4个方向,如果是0节点,则入栈,因为是可达的。1/2接线不可通过,不需再向下找
for(int k = 0; k < direct.length; k++) {
int newRow = row + direct[k][0];
int newCol = col + direct[k][1];
if(newRow >=0 && newRow < board.length
&& newCol >=0 && newCol < board[0].length) {
if ((board[newRow][newCol] == '.' || board[newRow][newCol] == 'T') && !flags.contains(new Pair<>(newRow, newCol))) {
queue.addLast(new Pair<>(newRow, newCol));
flags.add(new Pair<>(newRow, newCol));
}
}
}
}
return false;
}
public static int bfs(char[][] board, int[] box, int[] persion, int[] dest) {
//记录人可达集合
class Node {
int rowIndex;
int colIndex;
int dest;
public Node(int row, int col, int dest) {
this.rowIndex = row;
this.colIndex = col;
this.dest = dest;
}
}
//定义队列,需要查找距离,搜易需要记录遍历的节点的深度
ArrayDeque<Node> queue = new ArrayDeque<Node>();
//定义标志数组,找过的,不需要重复找。避免两个相邻的0节点互相找
HashSet<Pair<Integer, Integer>> flags = new HashSet<Pair<Integer, Integer>>();
//定义数组root关联节点的方向,互为相反方向
int[][] direct = new int[][]{{0, -1}, {0 ,1}, {-1, 0}, {1, 0}};
int[][] directX = new int[][]{{0, 1}, {0 ,-1}, {1, 0}, {-1, 0}};
queue.addLast(new Node(box[0], box[1], 0));
flags.add(new Pair<>(box[0], box[1]));
while(!queue.isEmpty()) {
Node node = queue.pollFirst();
int row1 = node.rowIndex;
int col1 = node.colIndex;
if (row1 == dest[0] && col1 == dest[1]) {
return node.dest;
}
//推导箱子在此位置
board[row1][col1] = 'B';
for(int i = 0; i < direct.length; i++) {
int newRow = row1 + direct[i][0];
int newCol = col1 + direct[i][1];
int persionRow = row1 + directX[i][0];
int persionCol = col1 + directX[i][1];
if(newRow >0 && newRow < board.length
&& newCol >0 && newRow < board[0].length
&& persionRow >0 && persionRow < board.length
&& persionCol >0 && persionCol < board[0].length) {
int[] dst = new int[]{persionRow, persionCol};
if((board[newRow][newCol] == '.' || board[newRow][newCol] == 'T' )
&& persionArrived(board, persion, dst)
&& !flags.contains(new Pair<>(newRow, newCol))) {
queue.addLast(new Node(newRow, newCol, node.dest +1));
flags.add(new Pair<>(newRow, newCol));
}
}
}
//清空推导中临时的箱子位置
board[row1][col1] = '.';
}
return -1;
}
结果:
如下问题,绿色点需要走两次,但是通过flags标识后,导致[4]/[4]->[3]/[5]无法走。
- 如果不打标签,会导致死循环。
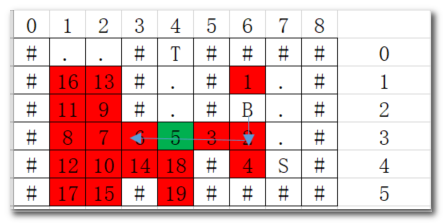
【优化】:
标签中加入经过一个Node的方向,同一方向不允许重复。
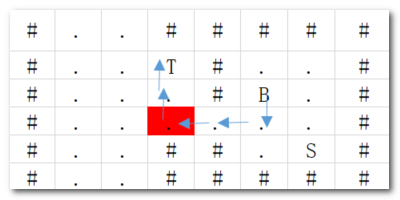
仍然报错,如下:当箱子在绿点,S位置到紫点不可达,导致[2]/[4]位置无效,所以要记录上次Persion的位置。
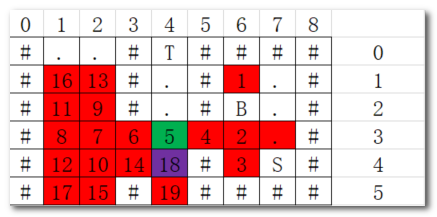
public static int bfs(char[][] board, int[] box, int[] persion, int[] dest) {
//记录人可达集合
class Node {
int rowIndex;
int colIndex;
int dest;
public Node(int row, int col, int dest) {
this.rowIndex = row;
this.colIndex = col;
this.dest = dest;
}
}
//定义队列,需要查找距离,搜易需要记录遍历的节点的深度
ArrayDeque<Node> queue = new ArrayDeque<Node>();
//定义数组root关联节点的方向,互为相反方向
int[][] direct = new int[][]{ {-1, 0}, {1, 0},{0, -1}, {0 ,1},};
int[][] directX = new int[][]{{1, 0}, {-1, 0},{0, 1}, {0 ,-1},};
int[][] count = new int[board.length][board[0].length];
//定义标志数组,找过的,不需要重复找。避免两个相邻的0节点互相找
//HashSet<Pair<Integer, Integer>> flags = new HashSet<Pair<Integer, Integer>>();
boolean[][][] flags = new boolean[direct.length][board.length][board[0].length];
queue.addLast(new Node(box[0], box[1], 0));
//flags.add(new Pair<>(box[0], box[1]));
flags[0][box[0]][box[1]] = true;
flags[1][box[0]][box[1]] = true;
flags[2][box[0]][box[1]] = true;
flags[3][box[0]][box[1]] = true;
while(!queue.isEmpty()) {
Node node = queue.pollFirst();
int row1 = node.rowIndex;
int col1 = node.colIndex;
if (row1 == dest[0] && col1 == dest[1]) {
return node.dest;
}
//推导箱子在此位置
board[row1][col1] = 'B';
if(row1 ==3 && col1 ==4) {
row1 =3;
}
if(row1 ==3 && col1 ==3) {
row1 =3;
}
for(int i = 0; i < direct.length; i++) {
int newRow = row1 + direct[i][0];
int newCol = col1 + direct[i][1];
int persionRow = row1 + directX[i][0];
int persionCol = col1 + directX[i][1];
if(newRow >0 && newRow < board.length
&& newCol >0 && newRow < board[0].length
&& persionRow >0 && persionRow < board.length
&& persionCol >0 && persionCol < board[0].length) {
int[] dst = new int[]{persionRow, persionCol};
if((board[newRow][newCol] == '.' || board[newRow][newCol] == 'T')
&& persionArrived(board, persion, dst)
&& flags[i][newRow][newCol] != true) {
queue.addLast(new Node(newRow, newCol, node.dest +1));
flags[i][newRow][newCol] = true;
}
}
}
//清空推导中临时的箱子位置
board[row1][col1] = '.';
}
return -1;
}
【优化】:入队列,除了记录节点,还需要记录当前Persion所在位置。
public static boolean persionArrived(char[][] board, int curPersonRow, int curPersonCol, int destRow, int destCol) {
//定义队列,需要查找距离,搜易需要记录遍历的节点的深度
ArrayDeque<Pair<Integer, Integer>> queue = new ArrayDeque<Pair<Integer, Integer>>();
//定义标志数组,找过的,不需要重复找。避免两个相邻的0节点互相找
HashSet<Pair<Integer, Integer>> flags = new HashSet<Pair<Integer, Integer>>();
//定义数组root关联节点的方向
int[][] direct = new int[][]{{0, -1}, {0 ,1}, {-1, 0}, {1, 0}};
//Pair tmpPair = new Pair<>(cur[0],cur[1]);
queue.addLast(new Pair<>(curPersonRow,curPersonCol));
flags.add(new Pair<>(curPersonRow,curPersonCol));
while(!queue.isEmpty()) {
Pair node = queue.pollFirst();
int row = (Integer)node.getKey();
int col = (Integer)node.getValue();
if(row == destRow && col == destCol)
{
return true;
}
//遍历4个方向,如果是0节点,则入栈,因为是可达的。1/2接线不可通过,不需再向下找
for(int k = 0; k < direct.length; k++) {
int newRow = row + direct[k][0];
int newCol = col + direct[k][1];
if(newRow >=0 && newRow < board.length
&& newCol >=0 && newCol < board[0].length) {
if (board[newRow][newCol] != '#' && board[newRow][newCol] != 'B' && !flags.contains(new Pair<>(newRow, newCol))) {
queue.addLast(new Pair<>(newRow, newCol));
flags.add(new Pair<>(newRow, newCol));
}
}
}
}
return false;
}
public static int bfs(char[][] board, int[] box, int[] persion, int[] dest) {
//记录人可达集合
class Node {
int rowIndex;
int colIndex;
int dest;
int curPersonRow;
int curPersonCol;
public Node(int row, int col, int dest, int curPersonRow, int curPersonCol) {
this.rowIndex = row;
this.colIndex = col;
this.dest = dest;
this.curPersonRow = curPersonRow;
this.curPersonCol = curPersonCol;
}
}
//定义队列,需要查找距离,搜易需要记录遍历的节点的深度
ArrayDeque<Node> queue = new ArrayDeque<Node>();
//定义数组root关联节点的方向,互为相反方向
int[][] direct = new int[][]{ {-1, 0}, {1, 0},{0, -1}, {0 ,1},};
int[][] directX = new int[][]{{1, 0}, {-1, 0},{0, 1}, {0 ,-1},};
//定义标志数组,找过的,不需要重复找。避免两个相邻的0节点互相找
boolean[][][] flags = new boolean[direct.length][board.length][board[0].length];
queue.addLast(new Node(box[0], box[1], 0, persion[0], persion[1]));
flags[0][box[0]][box[1]] = true;
flags[1][box[0]][box[1]] = true;
flags[2][box[0]][box[1]] = true;
flags[3][box[0]][box[1]] = true;
while(!queue.isEmpty()) {
Node node = queue.pollFirst();
int row1 = node.rowIndex;
int col1 = node.colIndex;
int curPersonRow = node.curPersonRow;
int curPersonCol = node.curPersonCol;
if (row1 == dest[0] && col1 == dest[1]) {
return node.dest;
}
//推导箱子在此位置
board[row1][col1] = 'B';
for(int i = 0; i < direct.length; i++) {
int newRow = row1 + direct[i][0];
int newCol = col1 + direct[i][1];
int personRow = row1 + directX[i][0];
int personCol = col1 + directX[i][1];
if(newRow >=0 && newRow < board.length
&& newCol >=0 && newCol < board[0].length
&& personRow >=0 && personRow < board.length
&& personCol >=0 && personCol < board[0].length) {
if(board[newRow][newCol] != '#'
&& persionArrived(board, curPersonRow, curPersonCol, personRow, personCol)
&& flags[i][newRow][newCol] != true) {
queue.addLast(new Node(newRow, newCol, node.dest +1, row1, col1));
flags[i][newRow][newCol] = true;
}
}
}
//清空推导中临时的箱子位置
board[row1][col1] = '.';
}
return -1;
}
7)进击的骑士(力扣)
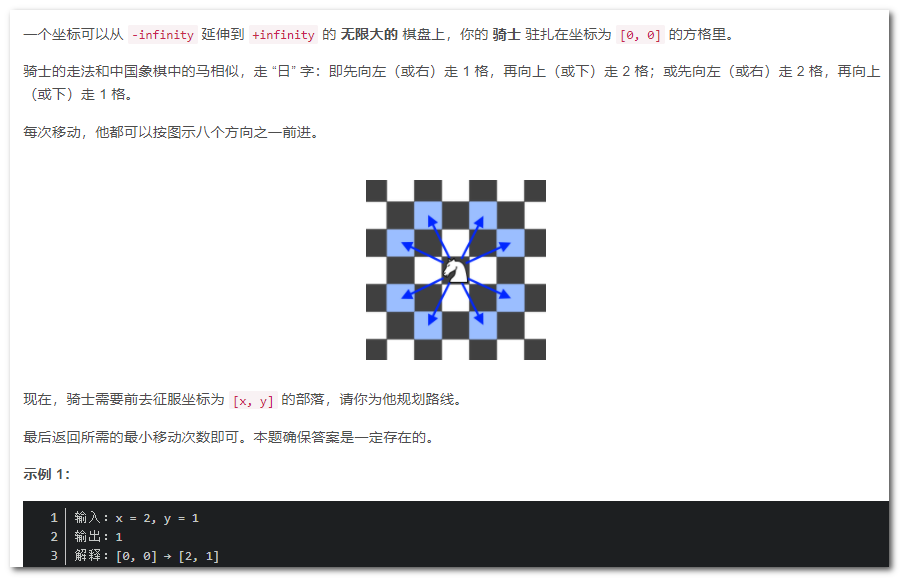
提示:
|x| + |y| <= 300
【分析】:
本地是的典型的BFS,从启动找终点最短路径:、
- 找下一级搜索节点,有8种类型[-1. -2]、[-1,+2]、[-2, -1]、[-2, +1]、[+1. -2]、[+1,+2]、[+2, -1]、[+2, +1]
- 原点是[0, 0],输入是目标节点。
- 如x=2或-2,则包含x节点的最小矩阵横坐标为-2/-1/0/1/2。推算:
收到x、y,定义矩阵大小为[2abs(x)+1] | [2abs(y)+1]。
输入的坐标全部按照横坐标+|x|,纵坐标+|y| 换算:骑士原点|x||y|、目标点x+|x|、y+|y|
8)公交路线
题目描述:
我们有一系列公交路线。每一条路线 routes[i] 上都有一辆公交车在上面循环行驶。例如,有一条路线 routes[0] = [1, 5, 7],表示第一辆 (下标为0) 公交车会一直按照 1->5->7->1->5->7->1->... 的车站路线行驶。
假设我们从 S 车站开始(初始时不在公交车上),要去往 T 站。 期间仅可乘坐公交车,求出最少乘坐的公交车数量。返回 -1 表示不可能到达终点车站。
【分析】
通过例子分析,假设有四辆公交:{{1,5,7}, {2,5,6}, {2,3,4}, {9,7,8},需要从7站点到4站点,可能得检索树为:
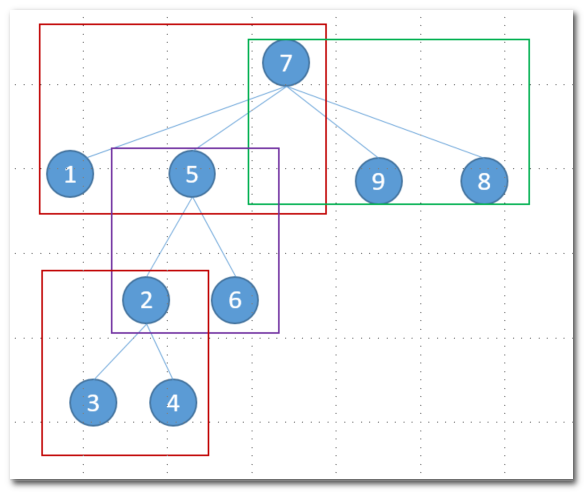
可以分析得出:
- 组成站点树
- BFS的下一层的检索关系,是经过当前站点的公交所经由的所有站点。
- 检索的换栈个数,就是树的检索深度。(root的深度是0)
输入是公交序列,如何快速的根据站点找到经过站点的公交序列呢?

源码参考:
public static int numBusesToDestination(int[][] routes, int source, int target) {
if(routes.length ==0 || routes[0].length ==0) {
return -1;
}
HashMap<Integer, ArrayList<Integer>> map = new HashMap<Integer, ArrayList<Integer>>();
for(int i=0; i < routes.length; i++) {
for(int j=0; j< routes[i].length;j++) {
if(!map.containsKey(routes[i][j])) {
map.put(routes[i][j], new ArrayList<>(Arrays.asList(i)));
}
else {
map.get(routes[i][j]).add(i);
}
}
}
if(!map.containsKey(source) || !map.containsKey(target)) {
return -1;
}
ArrayDeque<Pair<Integer, Integer>> queue = new ArrayDeque<Pair<Integer, Integer>>();
HashSet<Integer> flags = new HashSet<Integer>();
queue.addLast(new Pair<>(source, 0));
flags.add(source);
while(!queue.isEmpty()) {
Pair node = queue.pollFirst();
if((Integer) node.getKey() == target) {
return (Integer)node.getValue();
}
ArrayList<Integer> list = map.get(node.getKey());
if(list == null) {
continue;
}
for(Integer index: list) {
if(index < routes.length) {
for(int k =0; k< routes[index].length; k++) {
if(!flags.contains(routes[index][k])) {
queue.add(new Pair<>(routes[index][k], (Integer)node.getValue()+1));
flags.add(routes[index][k]);
}
}
}
}
}
return -1;
}
9)最短的桥
在给定的二维二进制数组 A 中,存在两座岛。(岛是由四面相连的 1 形成的一个最大组。)
现在,我们可以将 0 变为 1,以使两座岛连接起来,变成一座岛。
返回必须翻转的 0 的最小数目。(可以保证答案至少是 1 。)
示例 1:
输入:A = [[0,1],[1,0]]
输出:1
示例 2:
输入:A = [[0,1,0],[0,0,0],[0,0,1]]
输出:2
示例 3:
输入:A = [[1,1,1,1,1],[1,0,0,0,1],[1,0,1,0,1],[1,0,0,0,1],[1,1,1,1,1]]
输出:1
提示:
2 <= A.length == A[0].length <= 100
A[i][j] == 0 或 A[i][j] == 1
【思路】
我们通过对数组 A 中的 1 进行搜索,可以得到两座岛的位置集合,分别为 source 和 target。随后我们从 source 中的所有位置开始进行广度优先搜索,当它们到达了target中的任意一个位置时,搜索的层数就是答案。
So:
- 合并集,找打两个岛屿集合。
- 从一个集合“所有节点”开发BFS,知道目标节点在集合2中
注意:
- 设计到频繁检索,注意集合的深度问题。
- 初始如队列,可把Source岛屿的所有节点初始都加入到队列,Dept为0。找到的第一个另外岛屿节点,则Dept就最小。
力扣官方代码参考:
class Solution {
public int shortestBridge(int[][] A) {
int R = A.length, C = A[0].length;
int[][] colors = getComponents(A);
Queue<Node> queue = new LinkedList();
Set<Integer> target = new HashSet();
//集合1所有节点入BFS队里,集合2所有几点入Target集合。
for (int r = 0; r < R; ++r)
for (int c = 0; c < C; ++c) {
if (colors[r][c] == 1) {
queue.add(new Node(r, c, 0));
} else if (colors[r][c] == 2) {
target.add(r * C + c);
}
}
}
while (!queue.isEmpty()) {
Node node = queue.poll();
if (target.contains(node.r * C + node.c))
return node.depth - 1;
for (int nei: neighbors(A, node.r, node.c)) {
int nr = nei / C, nc = nei % C;
if (colors[nr][nc] != 1) {
queue.add(new Node(nr, nc, node.depth + 1));
colors[nr][nc] = 1;
}
}
}
throw null;
}
//遍历连个集合,第一个集合设置为1,第二个集合设置为2。
public int[][] getComponents(int[][] A) {
int R = A.length, C = A[0].length;
int[][] colors = new int[R][C];
int t = 0;
for (int r0 = 0; r0 < R; ++r0)
for (int c0 = 0; c0 < C; ++c0)
if (colors[r0][c0] == 0 && A[r0][c0] == 1) {
// Start dfs
Stack<Integer> stack = new Stack();
stack.push(r0 * C + c0);
colors[r0][c0] = ++t;
//上下左右,向外扩散,相连的设置t值 (第一个集合为1,第二个集合为2)
while (!stack.isEmpty()) {
int node = stack.pop();
int r = node / C, c = node % C;
for (int nei: neighbors(A, r, c)) {
int nr = nei / C, nc = nei % C;
if (A[nr][nc] == 1 && colors[nr][nc] == 0) {
colors[nr][nc] = t;
stack.push(nr * C + nc);
}
}
}
}
return colors;
}
public List<Integer> neighbors(int[][] A, int r, int c) {
int R = A.length, C = A[0].length;
List<Integer> ans = new ArrayList();
if (0 <= r-1) ans.add((r-1) * R + c);
if (0 <= c-1) ans.add(r * R + (c-1));
if (r+1 < R) ans.add((r+1) * R + c);
if (c+1 < C) ans.add(r * R + (c+1));
return ans;
}
}
10)腐烂的橘子
在给定的网格中,每个单元格可以有以下三个值之一:
值 0 代表空单元格;
值 1 代表新鲜橘子;
值 2 代表腐烂的橘子。
每分钟,任何与腐烂的橘子(在 4 个正方向上)相邻的新鲜橘子都会腐烂。
返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1。
示例 1:
输入:[[2,1,1],[1,1,0],[0,1,1]]
输出:4
【思路】---容易
BFS,以2为起点Node找橘子,找到了就腐烂,继续扩散寻找
- 以2为起点Node。
- 找Node的上、下、左、右;为1,则设置其值为2,并入队列;为0,则跳过。
- 直到队里处理完毕。
- 由于如果有橘子不会腐烂,返回-1。So,可以先遍历好的橘子总述,最终腐烂数和总数比较。




