【算法】前缀和

一、算法理解

前缀和概念：

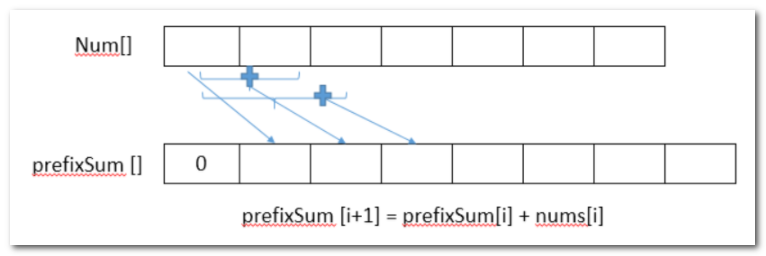
前缀和可以推导出两个变换公式：
两个变换公式：
（1）nums[某一项] = 两个相邻前缀和之差：nums[x] = prefixSum[x] - prefixSum[x - 1]
（2）从left 到 right的元素和等于 prefixSum[right+1] – prefix[left];

二、适用场景

求和为xxx的子数组。

四、使用案例

1）求和为k的子数组

给定一个整数数组和一个整数 k，你需要找到该数组中和为 k 的连续的子数组的 <个数>。
示例 1 :
输入:nums = [1,1,1], k = 2
输出: 2 , [1,1] 与 [1,1] 为两种不同的情况。

说明 :
数组的长度为 [1, 20,000]。
数组中元素的范围是 [-1000, 1000] ，且整数 k 的范围是 [-1e7, 1e7]。
代码实现提供三种算法，避免学习算法过程中思维被限制。

【思路1】
可以用滑窗。

    public int subarraySum(int[] nums, int k) {
        if(nums.length == 0) {
            return 0;
        }

        int tmpSum = 0;
        int subArrayNum = 0;

        for(int left = 0; left < nums.length; left++) {
            for(int right =left ; right < nums.length; right++) {
                tmpSum += nums[right];
                if(tmpSum == k) {
                    subArrayNum++;
                }
            }
            tmpSum = 0;
        }

        return subArrayNum;
    }

【思路2】：用前缀和。

计算前缀和
在前缀和上遍历i，j，使prefixNum[j] - prefixNum[i] = k。

    public int subarraySum(int[] nums, int k) {
        if(nums.length == 0) {
            return 0;
        }


        int[] prefixNum = new int[nums.length + 1];
        prefixNum[0] = 0;
        for(int i = 0; i< nums.length;i++) {
            prefixNum[i+1] = prefixNum[i] + nums[i];
        }

        int tmpSum = 0;
        int subArrayNum = 0;

        for(int left = 0; left < prefixNum.length; left++) {
            for(int right = left + 1 ; right < prefixNum.length; right++) {
                if(prefixNum[right] - prefixNum[left] == k) {
                    subArrayNum++;
                }
            }
        }

        return subArrayNum;
    }

2) 连续子数组和

给定一个包含 非负数 的数组和一个目标整数 k，编写一个函数来判断该数组是否含有连续的子数组，其大小至少为 2，总和为 k 的倍数，即总和为 n*k，其中 n 也是一个整数。

示例 1:
输入: [23,2,4,6,7], k = 6
输出: True
解释: [2,4] 是一个大小为 2 的子数组，并且和为6。

示例 2:
输入: [23,2,6,4,7], k = 6
输出: True
解释: [23,2,6,4,7]是大小为 5 的子数组，并且和为 42。

说明:
数组的长度不会超过10,000。
你可以认为所有数字总和在 32 位有符号整数范围内。

【思路1】：同上题，用滑窗
【思路2】：同上题，用前缀和

3) 可被 K 整除的子数组