【算法】差分

一、算法理解

差分，是一种和前缀和相对的策略。
如果有一数列 a[1],a[2],.…a[n]
且令 b[i]=a[i]-a[i-1], b[1]=a[1]

那么就有：
a[i] = b[1]+b[2]+.…+b[i] = a[1]+a[2]-a[1]+a[3]-a[2]+.…+a[i]-a[i-1]
此时b数组称作a数组的差分数组。

换句话来说a数组就是b数组的前缀和数组例：
原始数组a：9 3 6 2 6 8
差分数组b：9 -6 3 -4 4 2
可以看到a数组是b的前缀和

通过查分数组，在每一个点上记录变化数值，因为有增加有减少，通过求和判断 是否超过指定容量 的情况发生，超过则代表无法满足要求。

对于数组array[N]中的某一段进行增减操作，通过差分可在O（n）时间内完成。如
trips = [[2,1,5],[3,3,7]]；[2,1,5]表示第2个站点上车1个人、其在第5个站点下车
第一步：更新array[1] = 2, array[5] = -2;第一个站点上车2人占用两个座位，第5个站点下车2人，空出两个座位。
第二步：更新array[3] = 3, array[7] = -3;
第三步：进行求和,得到结果array[] = {0,2,2,5,5,3,3,0};

二、适用场景

线性上有增有减，通过求和 判断容量。比如：班车路线是否可容纳所有站点上下人需求。

三、注意事项

注意 差分数组下标 和 原始数组下标 的对应关系，比前缀和难理解一点。（B[i+1] = A[i+1]-A[i] ）。

四、使用案例

1）拼车

假设你是一位顺风车司机，车上最初有 capacity 个空座位可以用来载客。由于道路的限制，车只能向一个方向行驶
这儿有一份乘客行程计划表 trips[][]，其中 trips[i] = [num_passengers, start_location, end_location] 包含了第 i 组乘客的行程信息：

必须接送的乘客数量；
乘客的上车地点；
以及乘客的下车地点。
这些给出的地点位置是从你的初始出发位置向前行驶到这些地点所需的距离（它们一定在你的行驶方向上）。

请你根据给出的行程计划表和车子的座位数，来判断你的车是否可以顺利完成接送所有乘客的任务（当且仅当你可以在所有给定的行程中接送所有乘客时，返回 true，否则请返回 false）。
示例 1：
输入：trips = [[2,1,5],[3,3,7]], capacity = 4
输出：false
示例 2：

输入：trips = [[2,1,5],[3,3,7]], capacity = 5
输出：true
提示：

你可以假设乘客会自觉遵守 “先下后上” 的良好素质
trips.length <= 1000
trips[i].length == 3
1 <= trips[i]/[0] <= 100
0 <= trips[i]/[1] < trips[i]/[2] <= 1000
1 <= capacity <= 100000

【思路分析】：

每个站点就是原始序列。
每个站点上下人总数，就是差分序列。（这个题目，差分序列不是从原始序列计算得知，而是根据站点上下人得知）

代码样例：

    public static boolean carPooling(int[][] trips, int capacity){
        (trips.length == 0  || trips[0].length != 3 || capacity > 100000 || capacity < 0) {
            return false;
        }
        final int MAX_LOCATION = 1001;

        int[] Gaps = new int[MAX_LOCATION];
        for(int i = 0; i< trips.length; i++) {
            int person = trips[i][0];
            int startLocation = trips[i][1];
            int EndLocation = trips[i][2];

            if(startLocation < MAX_LOCATION && EndLocation < MAX_LOCATION) {
                Gaps[startLocation] += person;
                Gaps[EndLocation] -= person;
            }
        }

        int sum = 0;
        for(int j=0; j<MAX_LOCATION; j++) {
            sum += Gaps[j];
            if(sum > capacity)
                return false;
        }

        return true;
    }

2）航班预定

这里有 n 个航班，它们分别从 1 到 n 进行编号。
有一份航班预订表 bookings ，表中第 i 条预订记录 bookings[i] = [firsti, lasti, seatsi] 意味着在从 firsti 到 lasti （包含 firsti 和 lasti ）的每个航班上预订了 seatsi 个座位。

请你返回一个长度为 n 的数组 answer，其中 answer[i] 是航班 i 上预订的座位总数。
示例 1：

输入：bookings = [[1,2,10],[2,3,20],[2,5,25]], n = 5
输出：[10,55,45,25,25]
解释：
航班编号 1 2 3 4 5
预订记录 1 ： 10 10
预订记录 2 ： 20 20
预订记录 3 ： 25 25 25 25
总座位数： 10 55 45 25 25
因此，answer = [10,55,45,25,25]

public static int[] corpFlightBookings(int[][] bookings, int n){
    if(bookings.length == 0  || bookings[0].length != 3 || n <= 0) {
        return new int[0];
    }

    int[] Fights = new int[n];
    for(int i = 0; i< bookings.length; i++) {
        int startFlight = bookings[i][0];
        int endFlight = bookings[i][1];
        if(startFlight > 0 && startFlight <= 5 && endFlight > 0 && endFlight <= 5 ) {
            for(int j = startFlight - 1; j < endFlight; j++) {
                Fights[j] += bookings[i][2];
            }
        }
    }

    return Fights;
}

3）★★★★买卖股票的时机（超时）

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择某一天买入这只股票，并选择在未来的某一个不同的日子卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：
输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：
输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

【分析】：

获取差分
从差分中通过滑窗计算合值最大的连续片段。（滑窗）

代码参考：

    public int maxProfit(int[] prices) {
        if(prices.length == 0) {
            return 0;
        }

        int[] tt = new int[prices.length];
        tt[0] = 0; //prices[0];
        for(int i = 1; i<prices.length;i++ ) {
            tt[i] = prices[i] - prices[i-1];
        }

        int maxProfit = 0;
        int sum = 0;
        for(int start = 0; start< tt.length; start++) {            
            sum = 0;
            if(tt[start] <= 0 || (start > 0 && tt[start-1] > 0)){
                continue;
            }

            for(int end = start; end< tt.length; end++) {
                sum += tt[end];
                maxProfit = Math.max(maxProfit, sum);
            }
        }

        return maxProfit;
    }

如上计算超过时间限制。

【分析】：
1.简单的说：遍历，记录遍历过的最低点，求最低点和遍历点差值的最大数。

public static int maxProfit(int[] prices){
        if(prices.length == 0) {
            return 0;
        }
        
        int minprice = Integer.MAX_VALUE;
        int maxprofit = 0;
        for (int i = 0; i < prices.length; i++) {
            //刷新最低点
            if (prices[i] < minprice) {
                minprice = prices[i];
            }
            //随着遍历，计算后续节点与已知最低点差值
            if(prices[i] > minprice) {
                maxprofit = Math.max(maxprofit, prices[i] - minprice);
            }
        }
        return maxprofit;
    }

4）买卖股票最佳时机

分析：
不能同时参与多笔交易的意思就是：
比如：[7,1,5,3,6,4] 第2天买、第4天买，第5天卖，则是[5]-[4] + [5]-[2]，不允许这样，这样是不符合差分的。
要求的是：如第1天买、第3天卖、第4天再买、第6天卖，则是[3] - [1] + [6] -[4]。

【思路】

按照原始序列，形成差分
因为允许多次买卖，所以差分中是正数的两天都买卖一次购票，赚取所有正的差值。

代码参考

    public static int maxProfit(int[] prices){
        if(prices.length == 0) {
            return 0;
        }

        int[] tt = new int[prices.length];
        tt[0] = 0; //prices[0];
        for(int i = 1; i<prices.length;i++ ) {
            tt[i] = prices[i] - prices[i-1];
        }

        int maxProfit = 0;
        for(int start = 0; start< tt.length; start++) {
            if(tt[start] > 0) {
                maxProfit +=tt[start];
            }
        }

        return maxProfit;
    }

6）★会议室

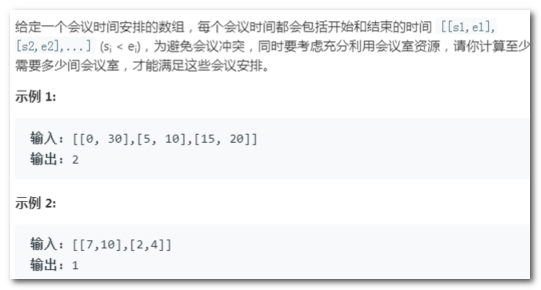
【思路】：

典型的差分（同上下车），计算最大值。
没有给出时间范围，建议可以用<time，会议室数量>结构保存，time为key，最大限度减少内存。