【算法】并查集
一、算法理解
并查集:给定一组元素,及其元素之间的关系,把存在直接、间接关系的元素组成一个集合。常用于解决如下类的问题:
(1)存在几个集合?
(2)最大集合容积?
(3)判断A、B是否在一个集合内?
样例场景【朋友圈】:一个班级有56名学生,存在直接好友关系(A、B是好友关系)、间接好友关系(A、B是好友,B、C是好友,则A、C是间接好友)的同学形成一个朋友圈。问:这个班级一共有几个朋友圈?
并查集主要有3个基本操作:
- makeSet(size):建立一个管理并查集的空间,包含 size 个集合元素。该操作通常比较隐晦,常用数组句int[] parent = new int[size] 直接替代makeSet。
- unionSet(x, y):把元素 x 和 y 所在“集合”合并成一个"集合",要求 x 和 y 所在原集合不相交,如果相交则不合并。
- find(x):找到元素x所在的集合的“代表”(通常在“集合”中选一个根元素作为代表)。
- 该操作也可以用于判断两个元素是否在同一个集合,两个元素所在集合的“代表”是同一个,就表示在一个集合。
- find(x)有两种实现方法:一种是 递归,一种是 非递归形式。
【并查集的实现算法]:
- 常用int[] parent = new int[size]的 数组 来管理“并查集”结果。
- 每个“集合”都需要一个“代表”,集合中其他元素关联到这个 “代表”。
- 通常选择集合中某个元素来“代表”这个集合,该元素称为集合的"代表元"。
- 一个集合内所有元素组织成以 “代表元”为根 的树形结构。对于每一个元素x来说,parent[x]指向x在树形结构上的父亲节点,如果x是 根节点 则令 parent[x]指向自己,即parent[x] = x 。
- 对于find(x)操作,可以沿着parent[x]不断在树形结构中向上移动,直到到达根节点(parent[x]=x的节点)。
通过图示展示采用数组管理的并查集结构:
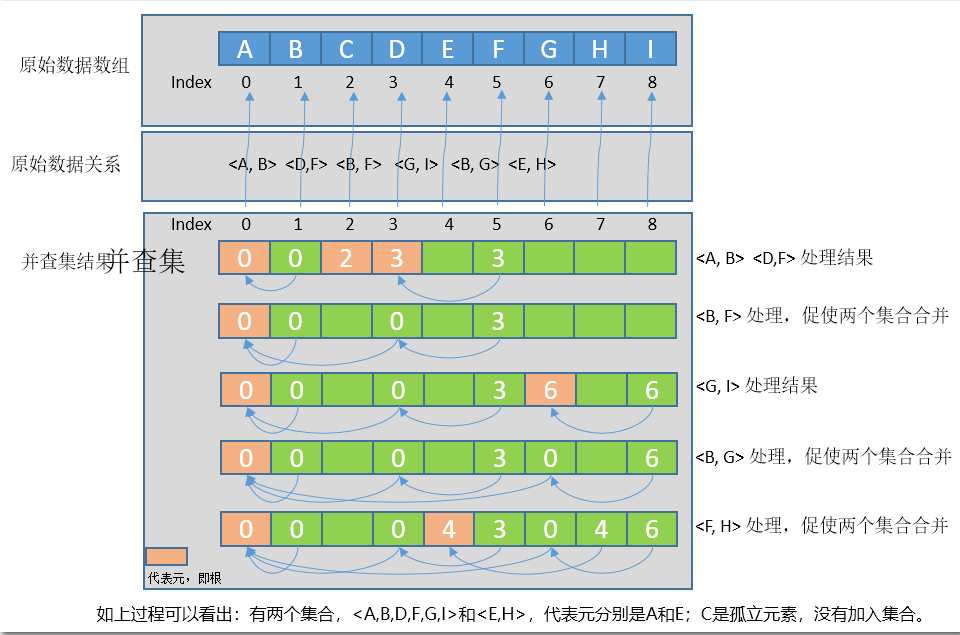
【注意】如上:
- 并查集数组中值 表示的是集合树关系。通过并查集数组下标<—>原始数据下标隐式表达结果 和 原始数据元素映射关系。
- 合并时,把集合2的“根节点” 变更成 指向 集合1“根节点”,即把集合2 挂到 集合1的根上。
【集合树均衡策略】
因为创建的集合树可能会严重不平衡,并查集可以用两种优化策略:
-
按秩合并 Union by Rank
“按秩合并”,即总是将更小的树连接至更大的树上。在这个算法中,术语“秩”替代了“深度”,因为同时应用了路径压缩时秩将不会与高度相同。 -
路径压缩 Path Compression
路径压缩:为了加快查找速度,查找时将x到根节点路径上的所有点的parent设为根节点,该优化方法称为压缩路径。
【并查集算法用途】:
- 维护无向图的连通性。支持判断两个点是否在同一连通块(集合)内。
- 判断增加一条边是否会产生环:用在求解最小生成树的Kruskal算法里。
二、注意事项
- 确认 孤立元素 是否 按照一个集合计算。此影响并查集 初始值 设置。如:
- 孤立元素作为一个集合。初始值可设置为-1,代表元也是值为-1的元素。孤立元素也是自身集合的代表元。
- 孤立元素不作为一个集合。初始值可设置为-1,代表元可设置为Index自身(u[index]==index)。
- 如果是求集合内元素个数,集合并完毕后,需遍历集合内元素,为统计效率需进行路径压缩(find时所有点的parent设为根节点)
三、使用案例
1. 【第一类】找集合个数
1)朋友圈
班上有N名学生。其中有些人是朋友,有些则不是。他们的友谊具有传递性。如果已知 A 是 B 的朋友,B 是 C 的朋友,那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈,是指所有朋友的集合。
给定一个 N * N 的矩阵 M,表示班级中学生之间的朋友关系。如果M/[i]/[j] = 1,表示已知第 i 个和 j 个学生互为朋友关系,否则为不知道。你必须输出所有学生中的已知的朋友圈总数。
示例 1:
输入: [[1,1,0],
[1,1,0],
[0,0,1]]
输出: 2
【思路分析】:
- 数组array[N]存放并查集分析结果。
- 单独一个学生也算一个朋友圈,所以数组初始值全部为-1,代表元也是值为-1。
- 遍历二维数组,如果M/[i]/[j] = 1,则Union(i, j)。
- 如果array[i]、array[j]都是-1,说明两个元素都没在任何集合,则合并为一个新集合:array[j]=i;
- 如果其中1个有集合,把无集合元素 挂到 已有集合根节点。
- 如果2个都有集合,则把array[j]的“根节点” 挂到 array[i]所在集合根节点(代表元)。
- 遍历array[],统计array[x] = -1的数量。
代码参考:
public static int findCircleNum ( int[][] matrix){
if (matrix.length == 0 || matrix[0].length == 0 || matrix.length != matrix[0].length) {
return 0;
}
int maxNum = matrix.length;
int[] retArray = new int[maxNum];
Arrays.fill(retArray, -1);
for (int i = 0; i < maxNum; i++) {
for (int j = 0; j < maxNum; j++) {
if (matrix[i][j] == 1 && i != j) {
union(retArray, i, j);
}
}
}
int retNum = 0;
for (int k = 0; k < maxNum; k++) {
if (retArray[k] == -1) {
retNum++;
}
}
return retNum;
}
public static void union (int[] retArray, int i, int j){
int iParent = findRoot(retArray, i);
int jParent = findRoot(retArray, j);
if(iParent != jParent) {
retArray[jParent] = iParent;
}
}
public static int findRoot(int[] retArray, int i) {
if(i < 0 || i > retArray.length) {
return -1;
}
int index = i;
while(retArray[index] != -1) {
index = retArray[index];
}
return index;
}
【扩展】如果不统计孤立元素,那么数组初始值-1,代表元为retArray[index]=index。如此:最终孤立元素值为-1,不会统计为集合。
代码差异点主要在:
- findRoot判断逻辑:find到的孤立元素,设置retArray[index]=index。
- 统计集合数条件。
public static int findCircleNum ( int[][] matrix){
if (matrix.length == 0 || matrix[0].length == 0 || matrix.length != matrix[0].length) {
return 0;
}
int maxNum = matrix.length;
int[] retArray = new int[maxNum];
Arrays.fill(retArray, -1);
for (int i = 0; i < maxNum; i++) {
for (int j = 0; j < maxNum; j++) {
if (matrix[i][j] == 1 && i != j) {
union(retArray, i, j);
}
}
}
int retNum = 0;
for (int k = 0; k < maxNum; k++) {
if (retArray[k] == k) {
retNum++;
}
}
return retNum;
}
public static void union (int[] retArray, int i, int j){
int iParent = findRoot(retArray, i);
int jParent = findRoot(retArray, j);
if(iParent != jParent) {
retArray[jParent] = iParent;
}
}
public static int findRoot(int[] retArray, int i) {
if(i < 0 || i > retArray.length) {
return -1;
}
//如果是孤立节点,需要刷新其值我index
if(retArray[index] == -1) {
retArray[index] = index;
}
int index = i;
while(retArray[index] != index) {
index = retArray[index];
}
return index;
}
2)冗余连接
输入一个图,该图由一个有着N个节点(节点值不重复1, 2, ..., N)的树及一条附加的边构成。附加的边的两个顶点包含在1到N中间,这条附加的边不属于树中已存在的边。
结果图是一个以边组成的二维数组。每一个边的元素是一对[u, v] ,满足u < v,表示连接顶点u 和v的无向图的边。
返回一条可以删去的边,使得结果图是一个有着N个节点的树。如果有多个答案,则返回二维数组中最后出现的边。答案边 [u, v] 应满足相同的格式 u < v。
样例:
输入: [[1,2], [1,3], [2,3]]
无向图为:
1
/ \
2 - 3
输出: [2,3]
【题目分析】:
- 本题目可以考虑:存在边关系的节点,加入并查集。如果遍历到某条边[x,y],发现x、y节点已经在一个集合中,则这个边就是多余的。
- “如果有多个答案,则返回二维数组中最后出现的边”,上例中,[1,2], [1,3], [2,3]中任何一个边当做多余边,都是可以的,但是要求给出最后出现的边。So,对输入的处理过程是从前->后。
源码参考:
public static int[] findCircleNum ( int[][] edges){
if (edges.length == 0 || edges[0].length != 2) {
return null;
}
int maxNum = edges.length * edges[0].length;
int[] retArray = new int[maxNum];
Arrays.fill(retArray, -1);
for (int i = 0; i < edges.length; i++) {
if (true == union(retArray, edges[i][0], edges[i][1])) {
return edges[i];
}
}
return null;
}
public static boolean union (int[] retArray, int i, int j){
int iRoot = findRoot(retArray, i);
int jRoot = findRoot(retArray, j);
if(iRoot != jRoot) {
retArray[jRoot] = iRoot;
return false;
}
return true;
}
public static int findRoot(int[] retArray, int i) {
if(i < 0 || i > retArray.length) {
return -1;
}
int index = i;
while(retArray[index] != -1) {
index = retArray[index];
}
return index;
}
3)岛屿数量
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1
【分析】:
- 这是个典型求集合个数的问题。
- 矩阵中每个点都是一个单独元素,用一个rowLength x colLenght长度的数组管理并查集。
- 孤立元素(0)的元素不做统计,代表元 和 孤立元素采用不同值。
- 合并条件是,[i][j]为1,并且上、左是1([i-1][j]/[i][j-1])。因为是从上到下、从做到右遍历,不需要判断下、右元素是否为1,后续会遍历到。
【注意】:
- 输入是"1"会转换成'1'字符比较,判断中用了数字1,导致未出结果。
- 自己处理中漏了一个场景,孤立的[1]点,这个时要设置arr[i] = i;但是不union;
- 自己和上、左元素比较时,选择了if-else if,“上”='1',则不再比较“左”,导致如下情况没处理
arr[2][1]和arr[1][1]比较了,arr[2][1]和arr[2][0]未比较,导致漏掉了arr[2][0]
[["1","1","0","0","0"],
["0","1","0","0","0"],
["1","1","1","0","0"],
["0","0","0","1","1"]]
代码参考:
public static int numIslands(char[][] grid) {
if (grid.length == 0) {
return 0;
}
int rowNum = grid.length;
int colNum = grid[0].length;
int maxNum = rowNum * colNum;
int[] retArray = new int[maxNum];
Arrays.fill(retArray, -1);
for (int i = 0; i < rowNum; i++) {
for(int j=0; j < colNum; j++) {
if(grid[i][j] == '1') {
int retIndex = i*colNum + j;
//先设置本节点为单点元素代表元,避免单点元素与无效元素混淆。
if(retArray[retIndex] == -1) {
retArray[retIndex] = retIndex;
}
//Here,上面,左边元素都需要比较
if(i > 0 && grid[i-1][j] == '1') {
union(retArray, (i-1)*colNum + j,retIndex);
}
if(j > 0 && grid[i][j-1] == '1') {
union(retArray, i*colNum + j -1, retIndex);
}
}
}
}
int sum = 0;
for(int k = 0; k < maxNum; k++) {
if(retArray[k] == k) {
sum += 1;
}
}
return sum;
}
public static void union (int[] retArray, int i, int j){
int iRoot = findRoot(retArray, i);
int jRoot = findRoot(retArray, j);
if(iRoot != jRoot) {
retArray[jRoot] = iRoot;
}
}
public static int findRoot(int[] retArray, int i) {
if(i < 0 || i > retArray.length) {
return -1;
}
int index = i;
while(retArray[index] != index && retArray[index] != -1) {
index = retArray[index];
}
return index;
}
4)句子相似性

【分析】:
- 把Pairs转换成并查集。
- 2个句子长度一致,否则不相似
- 对比两个句子中同一位置的单词,属于同一并查集(pairs中代表元相同),相似;否则(单词不在pairs中,或 两者不在同一并查集),不相似。
代码参考:
public static boolean numIslands(String[] words1, String[] words2, String[][] pairs) {
if(words1.length != words2.length) {
return false;
}
if(words1.length == 0) {
return true;
}
if(pairs.length == 0 || pairs[0].length == 0) {
return false;
}
int[] retArrays = new int[2 * pairs.length];
Arrays.fill(retArrays, -1);
ArrayList<String> allPairsWords = new ArrayList<String>();
for(int i=0;i < pairs.length; i++) {
if(allPairsWords.indexOf(pairs[i][0]) == -1) {
allPairsWords.add(pairs[i][0]);
}
if(allPairsWords.indexOf(pairs[i][1]) == -1) {
allPairsWords.add(pairs[i][1]);
}
union(retArrays, allPairsWords.indexOf(pairs[i][0]), allPairsWords.indexOf(pairs[i][1]));
}
for(int k=0;k < words1.length; k++) {
int rootIndex1 = allPairsWords.indexOf(words1[k]);
int rootIndex2 = allPairsWords.indexOf(words2[k]);
if(findRoot(retArrays, rootIndex1) != findRoot(retArrays, rootIndex2))
return false;
}
return true;
}
public static void union (int[] retArray, int i, int j){
int iRoot = findRoot(retArray, i);
int jRoot = findRoot(retArray, j);
if(iRoot != jRoot) {
retArray[jRoot] = iRoot;
}
}
public static int findRoot(int[] retArray, int i) {
if(i < 0 || i > retArray.length) {
return -1;
}
int index = i;
while(retArray[index] != index && retArray[index] != -1) {
index = retArray[index];
}
return index;
}
3.基于集合找路径中最小元素(力扣)
1) ★★★得分最高路径
【题目描述】:给你一个 R 行 C 列的整数矩阵 A。矩阵上的路径从 [0,0] 开始,在 [R-1,C-1] 结束。 路径沿四个基本方向(上、下、左、右)展开,从一个已访问单元格移动到任一相邻的未访问单元格。路径的得分是该路径上的最小值。例如,路径 8 → 4 → 5 → 9 的值为 4 。
找出所有路径中得分最高的那条路径,返回其得分。
【思路】:
使用一个同样大小的集合[n]/[m]来标注路径寻找过程。
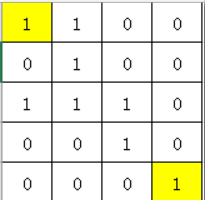
- 首先把[0]/[0]和[n]/[m]标注为1。
- 按照原始矩阵中各单元数值大小,从值 最大 的单元开始,逐个标准为1;(因为找的是最高分,所以从最大到小标准元素,只到[0]/[0]和[n]/[m]连通,其包含的元素值一定是所有路径中最大的)
- 标注过程中,如果存在上、下、左、右单元同样为1,则把这些同时为1的元素合并集。
- 直到[0]/[0]和[n]/[m]两个单元在一个集合中,找到这个路径(集合)中的最小元素。
【数据结构】:
- 需要一个包含n x m个元素的队列,记录元素在原始矩阵中的位置,然后根据矩阵中的值从小到大排序。用于后续从最大元素开始标注1。可以考虑采用数组,每个单元内容为原始矩阵的下标:
![image]()
- 一个新的[n]/[m]矩阵,里面元素的值只能是0、或1,默认全部是0,按照原始矩阵单元值,从大到小逐个标注为1,用于根据上、下、左、右是否为1,决定是否合并集。
- 一包含n x m个元素的队列,用于记录并查集树。其元素索引 和 原始[n][m]矩阵的关系是,其index = i*n+j。
代码实现如下:
//按照单个元素不选集合,需要统计最大集合数量书写逻辑
public static int findMinNum(int[][] lists) {
if(lists.length == 0 || lists[0].length == 0) {
return -1;
}
int rowNum = lists.length;
int colNum = lists[0].length;
//定义一个n*m元素的数组NodesList,每个单元值是原始矩阵中单元的坐标,通过原始矩阵中单元的值从大到小,对nodeLists进行排序,用于后续根据值大小在标注矩阵中逐个标注
Integer[] nodesList = new Integer[rowNum*colNum];
for(int j = 0; j < nodesList.length; j++) {
nodesList[j] = j; //j的下标,刚好是原始[n][m]矩阵坐标的i*cloNum + j
}
//按照其在原始矩阵中值按照从大到小排序
Arrays.sort(nodesList, (i, j) -> ((Integer)lists[j/colNum][j%colNum]).compareTo((Integer)lists[i/colNum][i%colNum]));
//创建Tags(标注)矩阵,默认值都是0,需查找的起点和终点是1
int[][] tags = new int[rowNum][colNum];
for(int i = 0; i < rowNum; i++) {
Arrays.fill(tags[i], 0);
}
tags[0][0] = 1;
tags[rowNum-1][colNum-1] = 1;
//创建合并集管理集合,默认值都是-1
int[] nodesTree = new int[rowNum*colNum];
Arrays.fill(nodesTree, -1);
//开始根据NodesList中顺序,按照原始矩阵中单元内值的从大到小,逐个在Tag[][]矩阵标注1,并把相邻的1单元合并集,直到[0][0]、[n-1][m-1]在同一集合
int tmpRowIdx = 0;
int tmpColIdx = 0;
int tmpRowDirIdx = 0;
int tmpColDirIdx = 0;
int rootNode1 = 0;
int rootNode2 = 0;
//定义一个上、下、左、右集合index计算的数组,用于下面for循环查找
int[][] dirs = new int[][]{{-1,0},{1,0},{0,-1},{0,1}};
int minNum = Math.min(lists[0][0], lists[rowNum-1][colNum-1]);
for(int l=0; l<nodesList.length;l++) {
//从大到小遍历到的节点标注1
tmpRowIdx = nodesList[l]/colNum;
tmpColIdx = nodesList[l]%colNum;
tags[tmpRowIdx][tmpColIdx] = 1;
//遍历当前节点上、下、左、右,看是否合并集
for(int m=0; m<dirs.length; m++) {
tmpRowDirIdx = tmpRowIdx + dirs[m][0];
tmpColDirIdx = tmpColIdx + dirs[m][1];
if(tmpRowDirIdx >= 0 && tmpRowDirIdx < rowNum
&& tmpColDirIdx >= 0 && tmpColDirIdx < colNum
&& tags[tmpRowDirIdx][tmpColDirIdx] == 1) {
union(nodesTree, nodesList[l],tmpRowDirIdx*colNum + tmpColDirIdx);
//每合并完一次,都检查是否联通
rootNode1 = findRoot(nodesTree, 0);
rootNode2 = findRoot(nodesTree, rowNum*colNum - 1);
//如果连通,直接找集合中最小路径
if(rootNode1 == rootNode2) {
for(int g=0; g<nodesTree.length; g++) {
if(findRoot(nodesTree, g) == rootNode1) {
minNum = Math.min(minNum, lists[g/colNum][g%colNum]);
}
}
return minNum;
}
}
}
}
return -1;
}
public static void union(int[] retArray, int i, int j){
int iRoot = findRoot(retArray, i);
int jRoot = findRoot(retArray, j);
if(iRoot != jRoot) {
retArray[jRoot] = iRoot;
}
}
public static int findRoot(int[] retArray, int i) {
if(i < 0 || i > retArray.length) {
return -1;
}
if(retArray[i] == -1) {
return i;
}
//【重点】刷新所有节点都挂载到根节点下,加快后续遍历并查集速度。
retArray[i] = findRoot(retArray, retArray[i]);
return retArray[i];
}
2)连通所有城市最小代价(力扣)
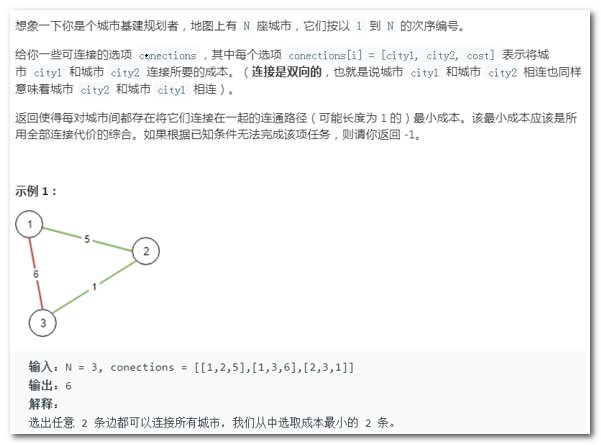
【思路】:
按照提供的路径代价从小到大排序,然后基于此顺序遍历输入的所有路径,直到所有城市成为1个集合。
注意点:
- 遍历某条路径时,如果发现两个城市已在1个合并集,忽略此多余路径。
- 数据结构:
输入:u[m][3]
中间数据结构:
(1)Integer[m],用于路径代价排序。
(2)cityList, 记录所有城市列表,建议用ArrayList。
(3)cityTree[],记录城市的并查集树,下标对应城市在cityList索引位置。
(4)int sumCort 累加联通代价。 - 过程
可以遍历原始数据过程中,边向cityList[]中添加记录,边进行cityTree合并集。
3)以图辨树(力扣)

【分析】
本质上就是根据edgs进行合并集,最终判断是否所有节点都在一个集合中。
注意:
- 最终要遍历所有节点的root相同,为了减低复杂度,find时要尽量减少树的深度(把所有节点的parent都刷新为root)。
4)最小等级字符(力扣)
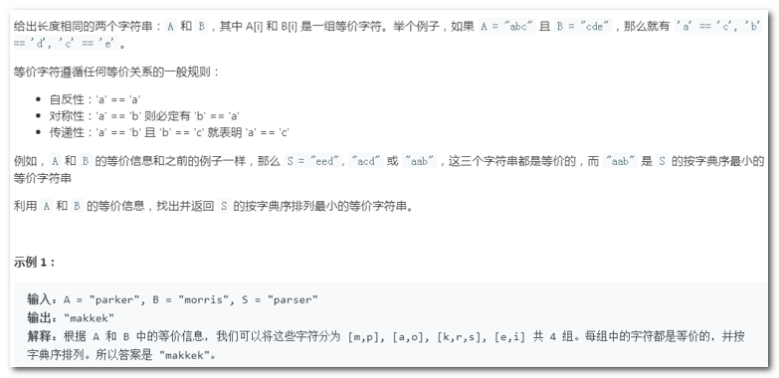
【思路】
- 遍历A、B字符串,把字符串中字符解析成多个合并集。
- 遍历合并集,把root节点调整为本合并集中最小元素。
- 把S字符串中每个字符替换为所在并查集的root。
5)无向图连通分量数目
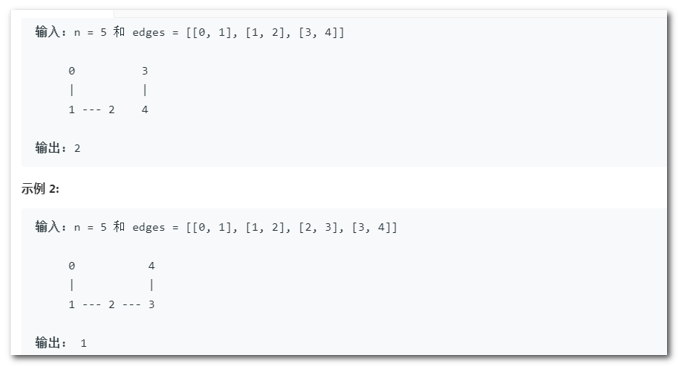
【分析】:
本质就上找最终合并集数目。
6)减少恶意软件传播

【分析】:
- 遍历initial中元素
- 把graph中对应元素位置置0,然后合并并查集,最终查询initial中剩余元素对应并查集大小。
- 重复1,找并查集最小的时刻。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号