软件工程第三次作业
一、问题描述
问题: 给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为: Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-2,11,-4,13,-5,-2)时,最大子段和为20。
求解:关于求最大子段和的问题,本次运用暴力求解、暴力求解的优化、
分治算法、遍历算法四种方法进行求解。
二、程序算法
public class getMaxpd {
/*
* 暴力求解法
*
* 列举出所有的字段和、选出最大字段和
*
* Run Time O(N^3)
*/
public static int getMaxpd1(int[] arr){
int maxSum = 0;
for(int i = 0; i < arr.length;i++) {
for(int j = i; j < arr.length;j++) {
int sum = 0;
for(int k = i; k <= j;k++) {
sum += arr[k];
}
if(sum > maxSum) {
maxSum = sum;
}
}
}
return maxSum;
}
/*
* 暴力求解法的改进
*
* 去掉最后一次的循环过程
*
* Run Time O(N^*2)
*/
public static int getMaxpd2(int[] arr) {
int maxSum = 0;
for(int i = 0; i < arr.length; i++) {
int sum = 0;
for(int j = i; j < arr.length;j++) {
sum += arr[j];
if(sum > maxSum) {
maxSum = sum;
}
}
}
return maxSum;
}
/*
* 分治算法三种情况:
* 1.最大的字段存在center以左
* 2.最大的字段存在center以右
* 3.最大的字段存在包括center的连续部分
*
* 找出后判断最大部分,用递归进行寻找
* Run Time O(N*logN)
*/
public static int getMaxpd3(int[] arr,int left,int right) {
if (left == right) {
if (arr[left] > 0) {
return arr[left];
} else {
return 0;
}
}
int center = (left+right)/2;
int maxLeftSum = getMaxpd3(arr,left,center);
int maxRightSum = getMaxpd3(arr,center+1,right);
//left-half's sum
int maxLeftAsideSum = 0,
leftAsideSum = 0;
for(int i = center; i >= left; i--) {
leftAsideSum += arr[i];
if(leftAsideSum > maxLeftAsideSum) {
maxLeftAsideSum = leftAsideSum;
}
}
//right-half's sum
int maxRightAsideSum = 0,
rightAsideSum = 0;
for(int i = center+1;i <= right; i++) {
rightAsideSum += arr[i];
if(rightAsideSum > maxRightAsideSum) {
maxRightAsideSum = rightAsideSum;
}
}
//has center sum
int centerSum = maxLeftAsideSum + maxRightAsideSum;
if(maxLeftSum > maxRightSum && maxLeftSum > centerSum) {
return maxLeftSum;
}else if (maxRightSum > maxLeftSum && maxRightSum > centerSum) {
return maxRightSum;
}else {
return centerSum;
}
}
/*
* 从Array的某一点,寻找到Array[i]的最大字段
* 置需要遍历一次数组
* Run Time O(N)
* The best in my functions
*/
public static int getMaxpd4(int arr[]) {
int maxSum =0,
sum = 0;
for(int i = 0; i < arr.length; i++) {
sum += arr[i];
if(sum > maxSum) {
maxSum = sum;
}else if(sum < 0) {
sum = 0;
}
}
return maxSum;
}
}
三、测试
(1)条件判定测试部分核心代码
public class getMaxpdTest {
@Test
public void testGetMaxpd0() {
int arr[] = {1,2,3,4,5,6};//全正用例
assertEquals(21,new getMaxpd().getMaxpd4(arr));
}
@Test
public void testGetMaxpd1() {
int arr[] = {1,2,-5,3,-15,4,5,-5,-1,2};//测试用例
assertEquals(9,new getMaxpd().getMaxpd4(arr));
}
@Test
public void testGetMaxpd2() {
int arr[] = {-1,-2,-100,-10};//全负测试用例
assertEquals(0,new getMaxpd().getMaxpd4(arr));
}
@Test
public void testGetMaxpd4() {
int arr[] = {-2,11,-4,13,-5,-2};//作业测试用例
assertEquals(20,new getMaxpd().getMaxpd4(arr));
}
}
(2)测试截图
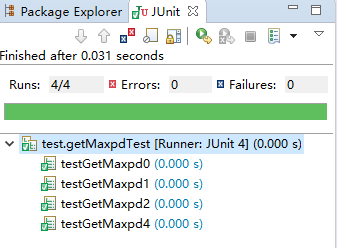
四、总结
a.算法的逐步优化应该是每一个程序员不断探索的。
b.学会将项目或代码上传到coding中,用于以后的学习、阅读。
c.测试部分应该全面,实现全面覆盖,对于软件开发和维护有很大价值。





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· PostgreSQL 和 SQL Server 在统计信息维护中的关键差异
· C++代码改造为UTF-8编码问题的总结
· DeepSeek 解答了困扰我五年的技术问题
· 为什么说在企业级应用开发中,后端往往是效率杀手?
· 用 C# 插值字符串处理器写一个 sscanf
· [翻译] 为什么 Tracebit 用 C# 开发
· 腾讯ima接入deepseek-r1,借用别人脑子用用成真了~
· DeepSeek崛起:程序员“饭碗”被抢,还是职业进化新起点?
· Deepseek官网太卡,教你白嫖阿里云的Deepseek-R1满血版
· 深度对比:PostgreSQL 和 SQL Server 在统计信息维护中的关键差异