行列式解二元方程组
上一章我们有一个方程组
我们将其转换为了矩阵形式
最左面的系数矩阵其实就是一个行列式，行列式使用竖线表示
这个三角形不是角，它是行列式的符号，代表着行列式。读作"德尔塔"，竖线同样是行列式的符号，用来代表行列式。
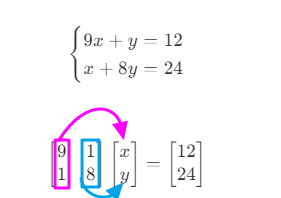
行列式的左列对应未知数x，右列对应未知数y
- 所以我们不需要在行列式中标出xy
- 对于最右面的矩阵我们不需要把他们放进行列式里。
所以最终这个方程组矩阵用行列式来表达的话就是这个样子
接下来说一说具体的解方程过程。
首先我们来画一个表格分析一下上面的方程组，在这个方程组的两个方程中等号右面都没有算式，所以我们称它这里列为常数列。
| 方程 | x列 | y列 | 常数列 |
|---|---|---|---|
| ① | 9 | 1 | 12 |
| ② | 1 | 8 | 24 |
我们使用行列式表示:
然后 我们将
- 行列式的左下角乘右上角得到结果a
- 行列式的左上角乘右下角得到结果b
- 最后将a减b
如下图所示
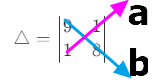
我们将a-b得到:
记住这个Δ，接下来我们继续之后我们要根据这个数字求出未知数x，y的具体数值。我们通常使用Δx，Δy，他们的意思就是代表行列式中的未知数x，y。
- 求Δx,y时我们依然使用刚才的方法，不过细节有些变化
- 当我们求Δx时，需要再x列替换为"常数列"
- 当我们求Δy时，需要再y列替换为"常数列"
首先我们求Δx
- 把原本的x列替换成常数列
- 然后相乘
接下来求Δy
- 把原本的y列替换成常数列
- 然后相乘
现在我们知道了这些：
- Δ=-71
- Δx=-72
- Δy=-204
现在让我们计算出真正的xy数值而不是Δ的xy数值。很简单，只需要将Δx,y除以Δ即可。
最后求xy：
让我们来验证一下，这个方程组解是否成立
可以看到，解是正确的。
我们使用矩阵法求二元方程时只需要3步:
- 分析各行列
- 行列式相乘得到Δ与Δxy
- 用Δxy除以Δ,得到xy
用行列式和矩阵求解时，对于矩阵本身来说是没什么作用的，他只是一个在数学中的表格，方便我们规划各行列。像我们用手画一个表格也可以，只不过矩阵更方便，我们不可能到哪里都有条件画个表格。
行列式解二元方程组
接下来再进一步讲解三元的方程组，三元方程组大概的思路和上面的二元一样，不过因为其未知数多了一个所以要稍微麻烦一点，只要熟练了也很快。
现在我们有一个三元方程组
我们使用矩阵分析行列式:
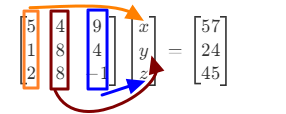
之后我们依然相乘不过这次更复杂：
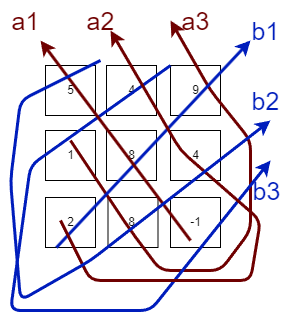
如图所示，我们只需要将(a1+a2+a3)得到的就是一个更抽象的a，b也同理。之后我们将a-b即可。
- a1=-1*5*8=-40
- a2=2*4*4=32
- a3=1*8*9=72
- b1=2*8*9=144
- b2=5*8*4=160
- b3=4*1*(-1)=-4
之后我们还要求出Δxyz
- Δx,接着用上面的方法，先乘在减：
- a1=-456,a2=720,a3=1728
- b1=3240,b2=1824.b3=-96
- Δy：
- a1=-120,a2=456,a3=405
- b1=432,b2=900,b3=-57
- Δz：
- a1=1800,a2=192,a3=456
- b1=912,b2=960,b3=180
最后用Δxyz除以Δ:
验证一下：
可以看到三元方程求解过程也差不多，无非就是相乘的路径复杂一些，不过只要你能跟着这个例子做完基本能够掌握了。注意，这种系数相乘的方法叫做"萨拉斯方法"而非十字相乘，他俩不是一个东西。
使用矩阵法无疑是最简单的一种，只需要会加减乘除就好了。当然了，我们也可以用"替代法、消除法、高斯消元法"，这些可以自己去找资源学。矩阵法的缺点就是只能算线性的也就是只能算一次的，所以需要化简变化成一次的...
最后还是那句话，我们遇到的方程几乎都不会吻合某个特定的公式，解方程其实最重要的是化简和变形而不是那些公式或是方法。
化简和变形就是一种逻辑思维，假如我们什么公式或是方法也不会，就只会基本的加减乘除一样可以把方程给它解出来，像是下面这种方程
我们就可以把等式两边-3，然后再同时除以2，就得到了x=2。面对复杂的方程变形就像是连连看，化简就像是消消乐。要么把化简变形后符合某个公式形式的方程套到公式里，要么就一直化简变形徒手解出来。
如果是实在学不进去数学也没关系，没有必要死磕，毕竟我们学的是电。不过就算学不进去也需要知道数学中有这个东西，就像这个矩阵法你可以不会算，但是大概的流程是什么你得知道，也得知道数学里有这个东西可以解决相应的问题，否则遇到了某个问题就算是给你个计算器你也不知道怎么算。
电桥电路
通常我们所说的电桥电路是指"惠斯通电桥"，如下图：
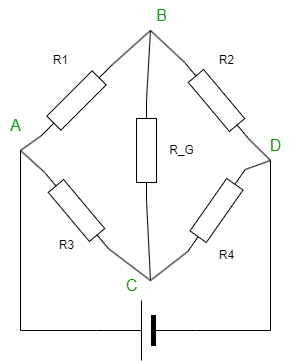
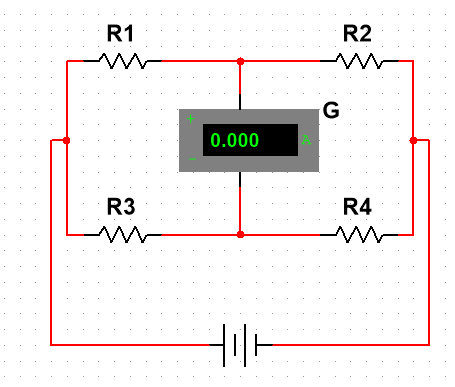
- G代表的"检流计"，这是可以把它看作是非常灵敏的电流表，可以有效的检测小电流。(由于仿真软件没这玩意，所以直接这里直接用电阻值非常低的电流表代替)
所谓的电桥电路就是电流分流到两个支路后又重新合并，从分流开始到合并的地方就叫做电桥电路，也就是上图中的A点到D点。电桥电路的作用就是测量一个元器件精确的电阻值。
- 被测元件放在R4的位置。
- 如果检流计的电流为0，就说明这个这个电桥是平衡的，只有平衡我们才能成功测量R4
检流计的电流是多少才能让电桥平衡呢？我们也可以用联立方程来推导出来。
首先我们分析这个电路，可以得出三个闭合电路。
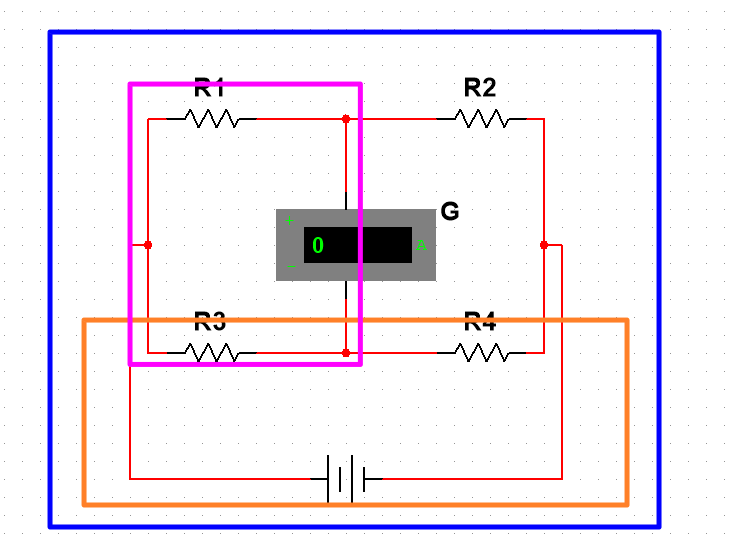
接下来再看看各闭合电路的电流如何流通的。
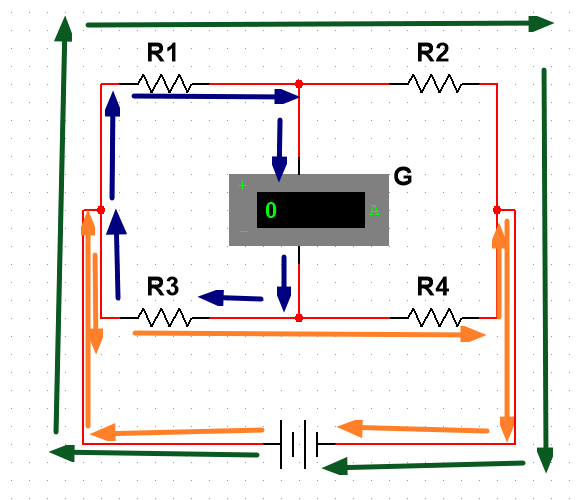
- 你可能会疑问蓝色电流没有造成短路或是什么不走R2或R4回到负极，因为绿色橙色已经走了。我们分出来的三个闭合电路实际上是一个等效电路，它并不存在只是方便我们分析。而蓝色橙色方向相反却在一根导线里，所以互相抵消。也就是说R3到R4的电流流动了但也流不动，因为在过程中被蓝色抵消了，蓝色也同理被橙色所抵消所以R3到R1的蓝色电流也一样被抵消了，就像是三相电星形接法的星点一样，虽然也可能会剩余一些电流但非常微小，除非R1和R2的电阻阻值差距过大。
现在我们根据基尔霍夫定律，写出各个闭合电路的电源电压(电动势)
-
绿色:
\[E_绿=R_1(I_绿+I_蓝)+R_2*I_绿 \]- 啥意思呢？
- 总算周知，电压的公式为V=I*R
- 而基尔霍夫电压守恒定律告诉我们，在一个闭合电路中，各负载的电压降之和等于电源电压(电动势)。
- 所谓的电压降我们上一章讲过了，就是我们平时说的电压，单位是V。
- 所以这个方程的意思就是绿色闭合电路的电源电压为R1的电压R2的电压。
- 为什么用电压？因为电流流动需要电压驱动，没有电压就没有电流，而绿色闭合电路的电流从R1和R2流过，因此我们只计算R1和R2的电压和。
-
橙色:
\[E_橙=R_3(I_橙-I_蓝)+R_4*I_橙 \]- 为什么是橙减蓝？因为橙色电流和蓝色电流相反。正极出发取+号，+号相反的电流取-号。
- 你也可以写成(+I_橙+-I_蓝)，例如1-1=0和(+1+-1=0),一个意思。
-
蓝色:
\[E_蓝=R_1(I_绿+I_蓝)+R_G*I_蓝+R_3(-I_橙+I_蓝) \]- 为什么这里橙色又变成负号了？
- 因为都一样，只是方便计算。我们上一章提到过交换律结合律，例如(-1+1)和(1+-1)一个意思。
- 之所以没事找事，是提醒各位在数学运算中要时刻的注意变形和化简，这样非常利于我们后续计算。
现在我们得到了三个方程，我们的目的是想要知道检流计的值到底是多少才能保证电桥平衡，那么我们需要这三个方程组成一个联立方程，之所以使用联立方程是因为我们有三个未知数也就是三条电流“橙蓝绿”，而且需要这三条电流的数值必须能同时够满足这三个方程的等式。因为这三个方程是我们抽象出来的等效电路，他们实际上并不存在。
可以看出来这是一个三元一次的方程组，但是现在这个方程组太丑了，如果直接放进矩阵里会让我们眼花缭乱，所以我们将这些方程按照其逻辑优化一下。
- 对于E绿:
- 原式:
\[E_绿=R_1(I_绿+I_蓝)+R_2*I_绿 \]- 首先R1和R2都被绿色电流流过所以
- 相当于(R1*绿+R2*绿),然后R1比较特殊，它同时被蓝色流过，所以我们需要把R1再乘上蓝色，最终就是
- 对于E橙:
- 原式:
\[E_橙=R_3(I_橙-I_蓝)+R_4*I_橙 \]- 橙色优化的步骤和绿色一样，最终就是
- 对于E蓝
-原式:\[E_蓝=R_1(I_绿+I_蓝)+R_G*I_蓝+R_3(-I_橙+I_蓝) \]- E蓝是最丑陋也是最复杂的，首先把每个负载都经过的电流都写出来找一下思路
\[E_蓝=（R_1*I_绿）+（R_1*I_蓝）+(R_G*I_篮)-(R_3*I_橙)+(R_3*I_蓝) \]- 这里因为电流蓝电流与橙电流方向相反，所以其电压也相反。
- 现在让我们看一下，首先我们把所有和蓝相乘的合并到一起，可以看到图中也是所有负载都被蓝色流过，所以这是合理的,所以就变成了:
\[E_蓝=R_1*I_绿-R_3*I_橙+(R_1+R_G+R_3)*I_蓝 \]- 虽然R1和R3没有关系，但是因为"R3*I橙"本来就是负的,所以不要动负号，本质是这样的
\[E_蓝=+（R_1*I_绿）++（R_1*I_蓝）++(R_G*I_篮)+-(R_3*I_橙)++(R_3*I_蓝) \]
现在把优化后的方程重新放入我们的联立方程中:
接下来放入矩阵，你也可以自己画一个表格,因为我们的1，2方程中并没有某些未知数的系数，所以把他们填0即可，"0*没有"等于0相当于没有
然后列出行列式Δ：
然后计算其结果Δ蓝电流:
- ΔI蓝：
最后求出真实的电流
- 蓝电流
其中我们只求I蓝的电流就好，因为蓝电流经过检流计。过程这里就省略了，流程和之前一样,感兴趣的可以自己试试。
- 总之我们知道蓝电流等于0才能让电桥平衡
- 因为E绿E橙实际上都是指电源电压可以统称为E，最后我们推导出的分数的的分子应该是\[\frac{(R_2*R_3-R_1*R_4)E}{.......} \]
- 那么我们就要证明这个分子必须等于0，才能证明当蓝电流等于0时才能让电桥平衡。
- 而根据基尔霍夫第二定律"闭合电路所有负载两端的电压之和必定等于0"
- 所以E蓝电流实际上就是它所有负载的两端电压之和，所以必定等于0。(看不懂可以回看我们之前最开始是怎样定义E蓝的方程的，之所以E蓝不等于E,是因为它并没有回到电源负极，因为E蓝被E橙抵消了，而E橙也被E蓝抵消了。所以实际上真正的电源电压E,是E绿，剩下的两个都在流动的过程中抵消)
- 所以当E等于0时就代表整个电路都没有电，所以E必须不能等于0
- 所以分子“(R2*R3-R1*R4)E”中，当E不等于0时，一定是括号中的某个被乘数为0或是被减数减去减数等于0
- 进一步得出（R2*R3-R1*R4）一定会等于0
- 最后我们我们可以根据（R2*R3-R1*R4）得出(R1*R4)一定等于(R2*R3)
- 这是因为a-b=0，那么a=b。例如1-1=0那么1=1，25-25=0所以25=25
总之我们最终得到了一个公式"R1*R4=R2*R3",现在有了这个公式我们就很容易明白电桥电路的意义了，之前说的那么多都不如这个公式有用。
假如我们四个电阻(负载都有电阻)，其中有一个我们不知道它的阻值是多少，那么此时我们就按照电桥电路搭配出一个电路，这样我们就可以使用得到的公式，根据任意三个已知的电阻求出未知的电阻阻值了,当然前提是我们需要确保电桥平衡，也就是检流计的电流为0，所以我们需要不断地调整其他三个电阻的阻值直到检流计的电流为0。
这种电桥电路通常都是应用于检测非常小的电阻，他比某些直接测电阻的器材更准确。
像是电阻表或万用表这种它们都是根据"偏位法"，而电桥电路时根据"零位法"。
我们可以把偏位法看作是电子秤，使用方便但是对精细的值不准确。零位法可以看作天枰，虽然需要长时间调整，但是当调准好后会十分准确。
最后对电桥电路做个总结
- 当R1R4=R2R3成立是那么就说明检流计所处的那条导线没有电压
- 因为没有电压，也就没有电流，电桥平衡
