之前我们在第三章的三相电粗略的提到过相量,其作用是来描述和计算交流电。
这一章我们将进一步的学习相量的原理。
虚数
虚数是一个虚无缥缈的想象数字,没有人能说清楚虚数的具体数值是多少(起码目前没有),但是我们可以使用一些方法判断虚数是否与某个数相等,这里暂时先不介绍了,之后我们学到。
通常虚数使用字母“j”来表示,虚数的定义是“平方数等于-1的数字”(在数学中通常使用字母i,但是在电路领域我们使用字母j,为了避免和交流电的电流混淆),如:
复数
此复数非彼负数。
我们之前说虚数是想象的数字,那么与之对应的就是实数(可以理解为实际存在的数字,关于实数是什么自己搜)。
而复数就是虚数和实数的结合体,也就是由想象的数字和实际的数字组合在一起的就是复数。
虚数的形式为(当然也有其他形式,但是在电气领域我们只使用这种):
a、b为实数,j为虚数。
- 其中+号左面的部分被称为"实部",因为它只有一个实数a
- +号右边的我们称之为"虚部",虽然这部分拥有实数b,但是因为它与虚数进行了运算,所以j*b这部分的结果也变得虚无缥缈了起来(虽然这部分是虚数但是b自身仍然是实数),所以称之为"虚部"
我们可以把a、b代入任何实数,比如:
相位
在学习三相电时我们提到过三相交流电之所以各相位间距120°,是因为三相交流发电机导体或者说是线圈将原来的单相交流发电机的导体呈120°分割为三份,这样在旋转的时候每一相都会被磁感线切割,从而使得整个三相电系统不会像单相电一样每运动完一个周期电力就会短暂中断。所以当发电厂的的电力输送到我们这里时我们得到的三相电就是每个相位间距120°。
这个间距被叫做相位差,用来描述两个相位之间的差。
所谓的相位就是表示一个相当前距离X轴正方向(通常为右边)的角度,例如下图中u相的相位就是45°。
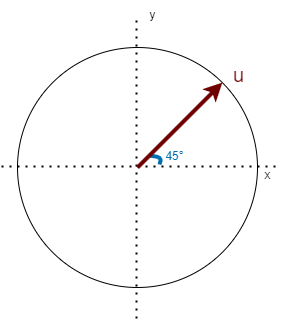
而相位差就是表示相与相之间相距多少角度,也就是用一个相的相位减去另一个相的相位,得到的差就是相位差。如下图
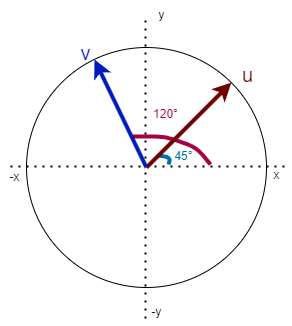
当我们计算u与v的相位差时就计算u的相位角度-v的相位角度。也就是
然而我们得到却是一个负数,这说明u相比v相落后75°,在这里正负代表着领先和落后。
当我们计算v与u的相位差时得到的是
这说明v相比u相领先,我们可以在波形图更直观的观察到。
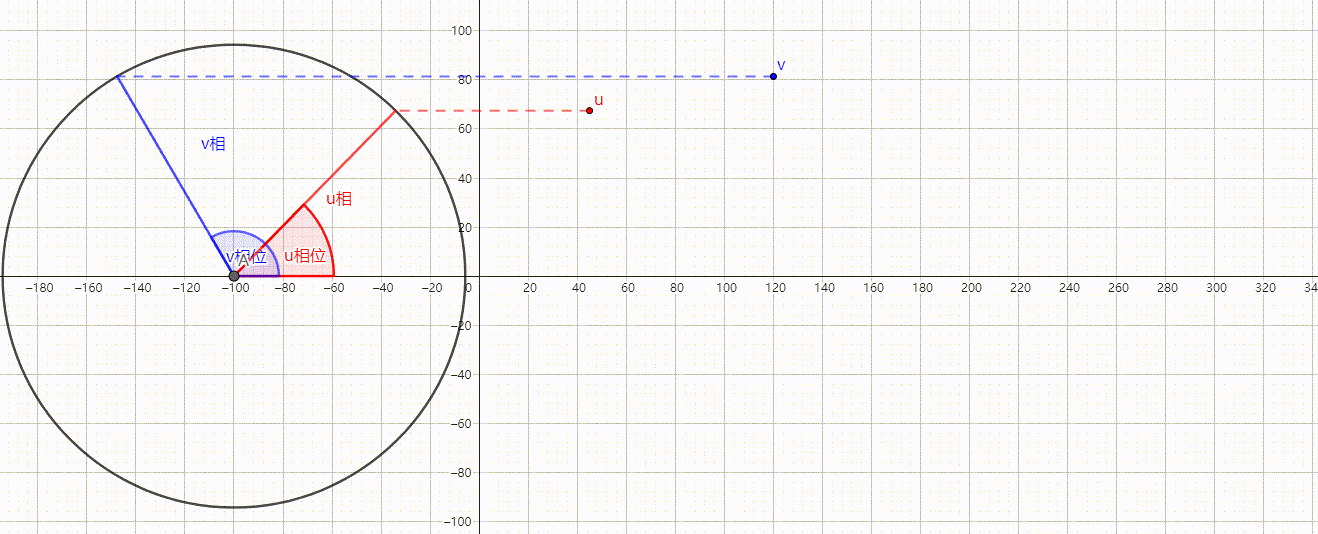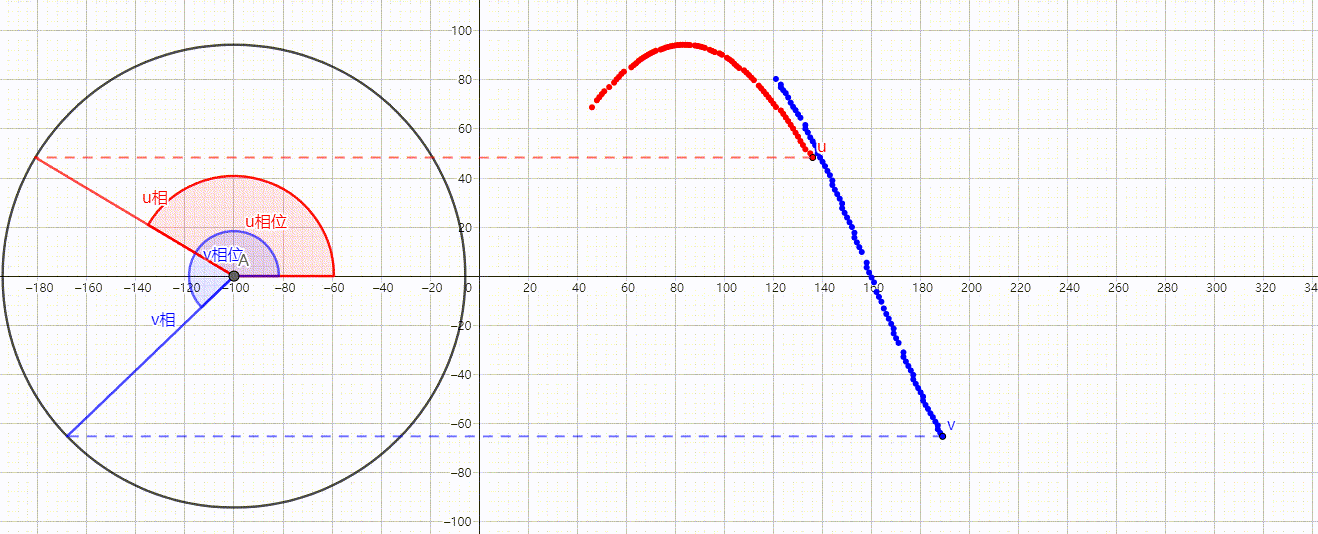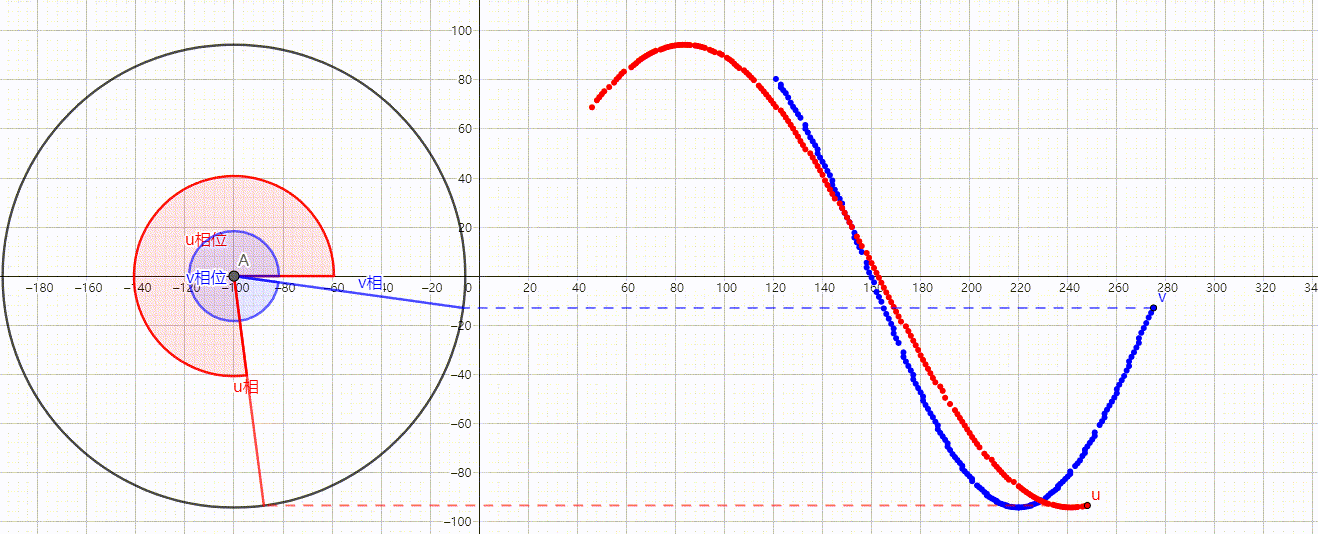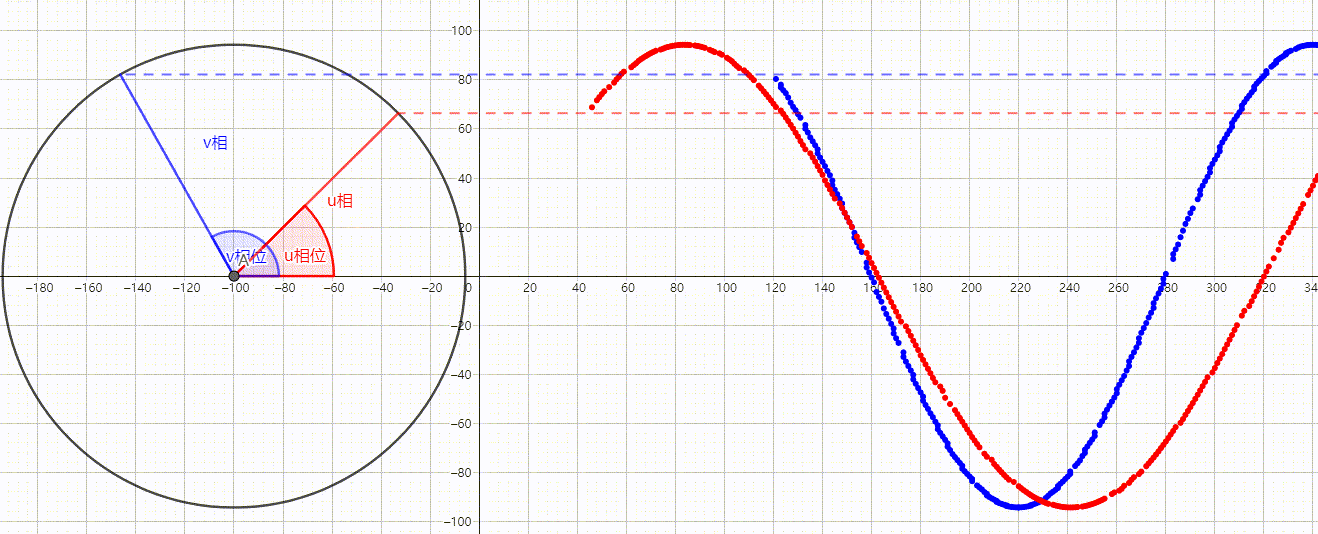
相
相很好理解,相在相量中就使用箭头箭头表示,它代表着电流或电压的状态,箭头的方向就是电流或电压的方向,箭头的长度就是电流或电压的大小。
为什么有了波形图还需要相量?
如果说只是查看电压或电流时,我们确实只使用波形图就足够了。
但是当我们想要同时查看电压电流时,把他们绘制在一个波形图上会导致十分混乱,因为电流的大小和方向并不总是和电压一致,尤其是在复杂的电路中。这个时候我们就可以借助相量轻松的表示出他们的状态,如下图。
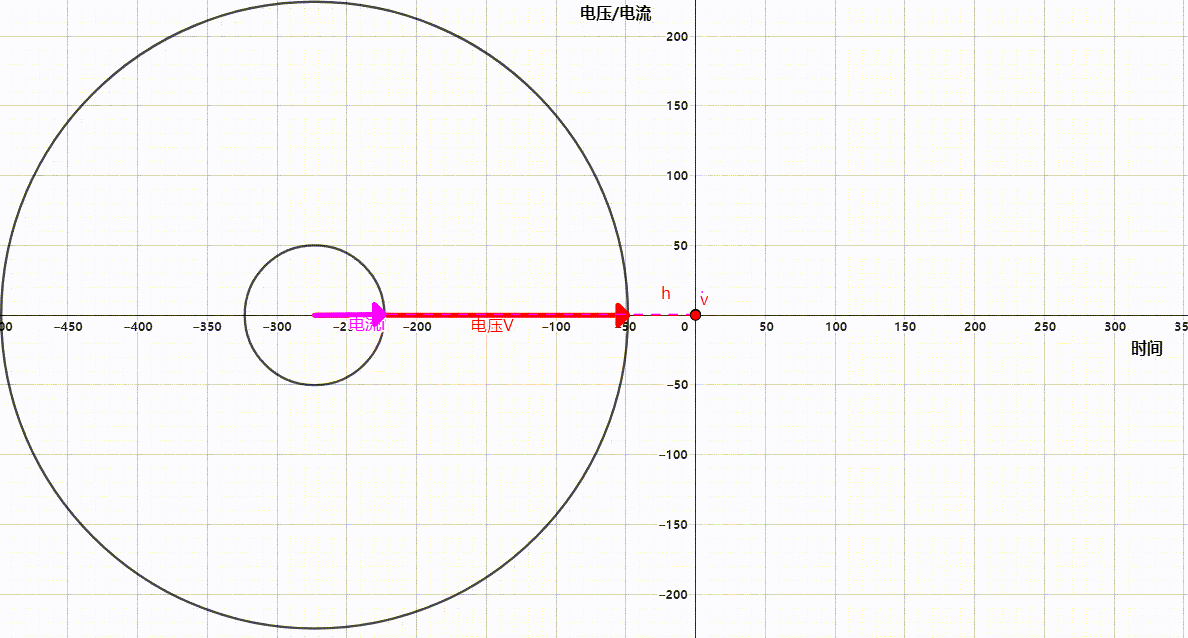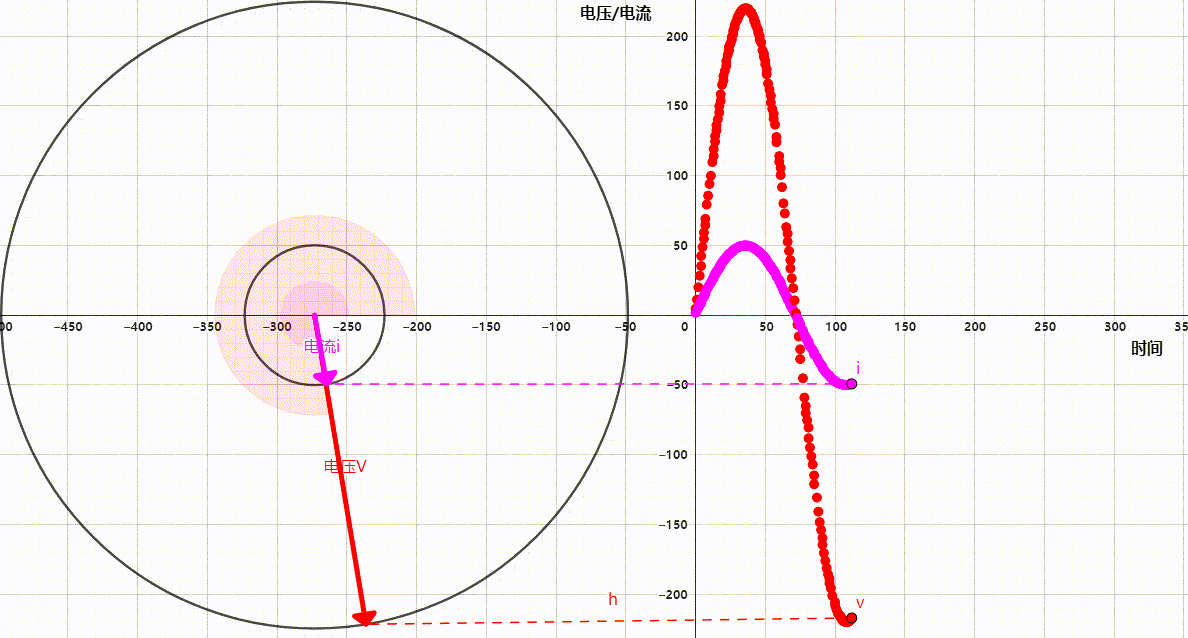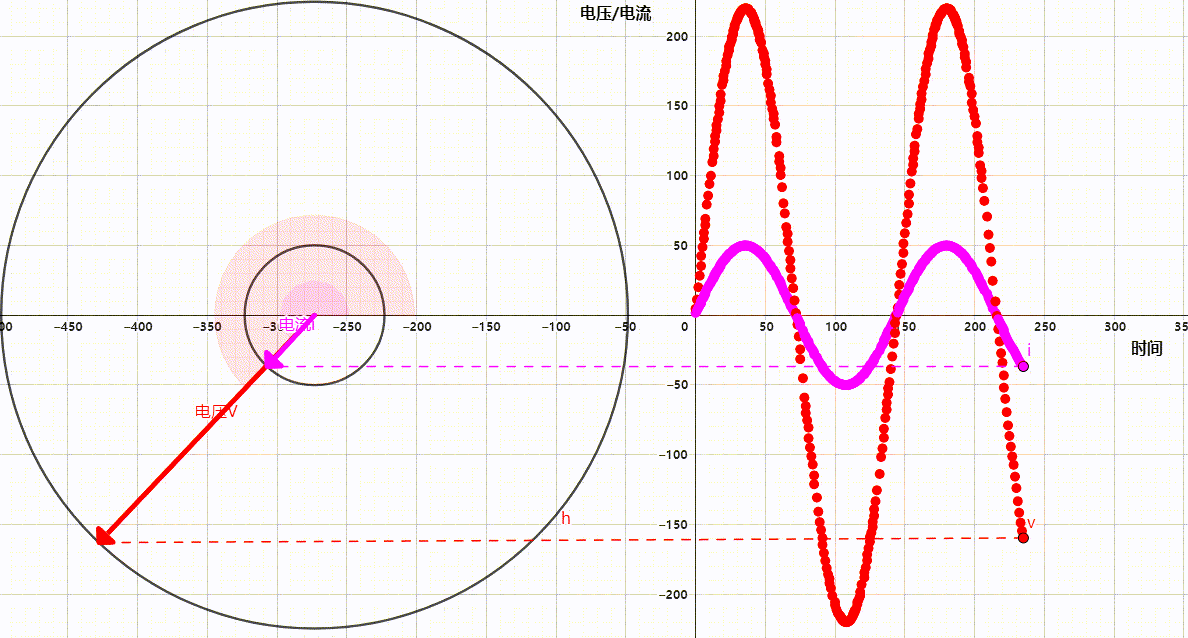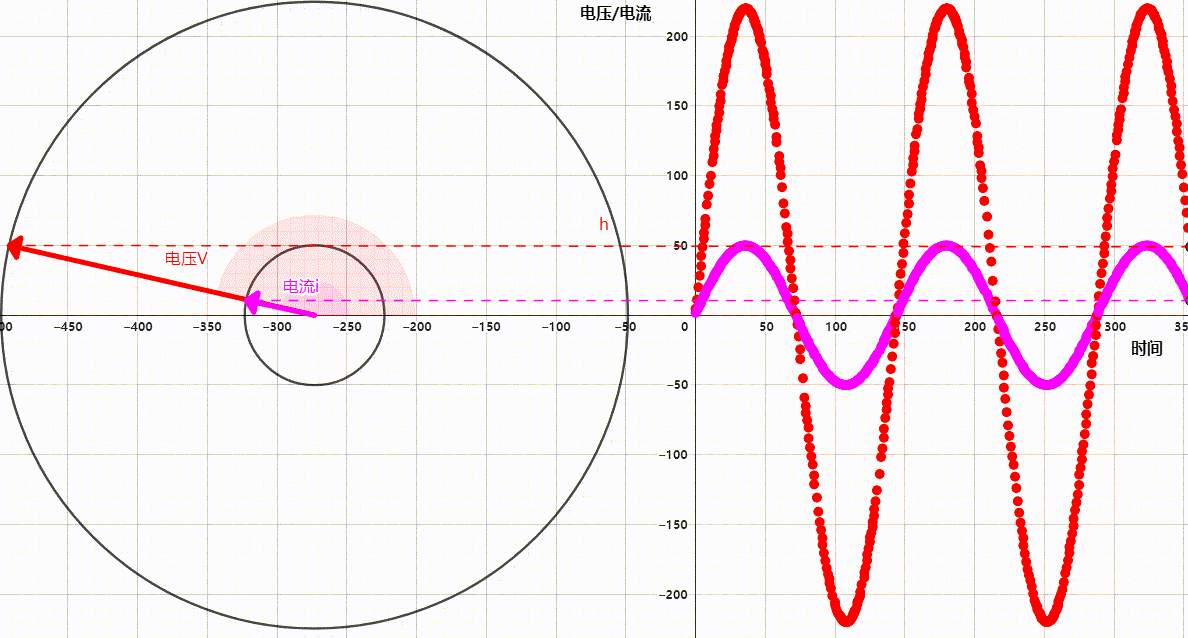
图中是单相交流电的220V电压和50A电流的相量与波形图描述,可以看出仅仅查看单相电波形图就已经有些复杂了更何况再复杂一些的多相电。而相量图则表示的十分清晰明了,大圆的半径时电压,直径是方向,小圆的半径是电流,直径是方向。
矢量与相量
在数学中向量通常是指一个既可以表示大小和方向的量,因为它与相量容易混淆,所以我们之后称向量为矢量。
首先要声明的是相量并不是数学中的矢量
矢量的英文为“vector”,相位的英文是"phase",他们合在一起才是相量的英文"phasor"。
我们可以把相量理解为一种旋转的的矢量,但是相量是专用于电路领域。换种说法就是矢量包括相量,但是相量不包括矢量。矢量可以做到的事相量只有在电路领域能够做到,而相量能够做的任何事矢量都可以做到。
我们也可以使用矢量来表示描述电压电流的状态,但是这显然是多此一举,因为使用矢量来表示描述电压电流或是正弦时,本质上是我们重新创造了一套相量。用程序员的说法就是重复造轮子。
代数中的相量
我们要得知相量每次都需要绘制相量图,这过于麻烦。我们可以使用开始时提到过的“复数”来表示相量(当然也可以用相量表示复数,不过我不觉得有人闲得慌来这么做)。
简单来说就是复数可以用来在数学中表示相量,这样我们就不用像之前一样真的去手动的画箭头了
首先我们要知道复平面,复平面就是一个用复数表示的二维的十字坐标图,其中
- 实数轴是我们平时熟知的横轴,也就是x轴,在复平面中我们称其为"Re"
- 虚数轴是竖轴,也就是y轴,在复平面中我们称其为"Im"
了解了复平面后我们就可以将"a+jb"的a和b的数值分别在坐标轴上标出。
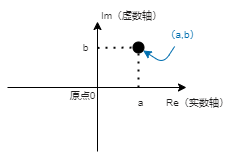
在描述一个坐标时,括号左面为横轴、右面为纵轴。
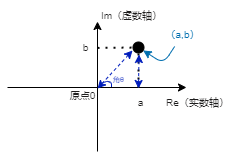
接下来我们就可以画个箭头来表示相量了(实际的数学运算有个点坐标就足够了,我在这里画箭头是为了方便理解)。

- 箭头从原点起始
- 指向点(a,b)
- 方向也可以用角度表示,以Re轴为起点,到点(a,b)的角度。通常我们使用"角θ"
![Image]()
最后我们来回顾一下我们学到的东西。
- 交流电的波形是三角函数的正弦波,同时这个正弦波能被复数计算出来。
- 相量既可以转换为正弦波也可以转换为复数,同时正弦波可以复原成相量,复数也可以复原成相量。
- 复数可以表示相量,同来进行相量的计算,同时也可以通过计算来复原正弦波
也就是说他们的特点或者优势就是:
- 正弦波可以直观的观测到时间,每秒的变化清晰可见,常用于排障和测试,但是在同时观测大量波形时又容易眼花缭乱。
- 相量是一个大杂烩,它可以非常直观的表示交流电的一切东西,所见即所得。但是需要配合三角函数或其他东西手动的切圆,十分麻烦。
- 复数的复平面是丐版相量,麻雀虽小五脏俱全,十分方便进行数学运算。有了它我们就可以暂时的逃避微积分和傅里叶变换(早晚还是要学的..),不过既然有简单快捷的路当然是抄近路最好。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号