一般来讲经过前几章的学习电气电路的基础我们已经学完了，也就是:
- 串联并联
- 电流电压电阻
- 交流电直流电
- 三相电与相线电压电流
- 星、三角接法
学会了这些我们基本能够看懂一个电路图，再之后的就是需要认识了解
- 各种元器件
- 复杂的电路网络
电气说简单也简单，无非就是上面那些东西，但是说难也难。难就难在它太简单，之后我们要学习的所有高级电气知识都要基于以上这些的基础组合而成。就像是你刚学会加减乘除就要学微积分一样。以我们现有的水平还没有资格真正的迈进电气领域的门槛。
电气中的数学
数学可以看作是一个语言，我们从小学习的三大主科"语文、外语、数学"，可以分别视为"与同文化的人沟通的语言、与外部文化的人沟通的语言、与物质世界沟通的语言"。
想要学好电，我们就要利用数学这门语言更深刻的进行了解。再说的宽泛一点，无论你学习任何知识，如果想要精进深入都无法逃避数学。
所以再更深入的学习电气之前，我们需要巩固一下自身的数学知识，否则在接下来的学习中我们面对各种符号和跳跃式的逻辑就像是在看魔咒一般头晕眼花，同时这一章也起到了巩固我们之前学习的内容的作用。
基础的术语
首先我们要学习电气中的各种术语，学会使用统一标准的术语，这样我们才能在与人或抽象的东西沟通时彼此知道对方说的是什么意思。
电位差/电压:
关于电位差我们可以用水的流动来形象的理解
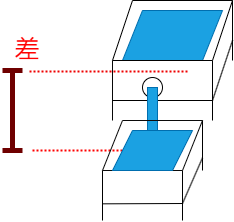
我们都知道水会从高处往低处流动，这是由于压力，在图中两箱水的高度距离越大，压力越大，从而流出的水流越多，我们称之为水位差。
而电也相同，电位差的大小决定着电流的流量，电位差越小，电流越小，电位差越大，电流越大。我们同时也称电位差为"电压"。
也就是说，所谓的电压就是让电产生流动的压强。
电流
电流就是指1秒内流经的电量。
电功率
电功率就是指电流在一秒内完成的工作量。
电阻
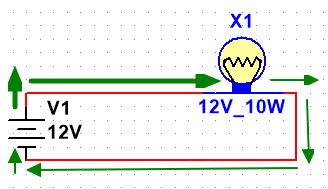
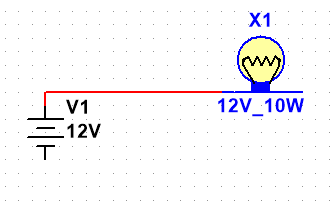
在上图中，我们的电源就是提供电压的设备，它产生了12V的电压来驱动电流流动，当电流流经负载(或者说是用电器，这里指灯泡)时，灯泡将电能转换为光能。
但是在电流经过负载时，负载同样的阻碍了电流的流动，就像是往小溪里放了块石头一样。所以在电流经过负载以后，其流量变小。
这个石头起到的就是阻碍电流流动，迫使电流流量减少的作用。这就是电阻。
每一个负载都有电阻，包括开关(只是可以忽略不计)。
不过与现实中的石头不同，我们的负载元件不只是阻碍电流，它在电流流过自身的同时，将电能转换为其他能量。就算是电阻元件，也有把电能转换为热能的作用。
额定电压
在图中负载标出了12V的标签，负载所标出的电压一般都是指额定电压，意思就是该负载在电压达到12V时达到最大的电功率，形象点说就是在电压达到12V时工作的效率最高，超过12V就会出问题，低于12V工作效率会变低也就是亮度降低。
符号
| 名称 | 符号 | 单位 |
|---|---|---|
| 电压 | V或E | V(伏特) |
| 电流 | I | A(安培) |
| 电阻 | R | \(\Omega\)(欧姆) |
| 电功率 | P | W(瓦特) |
电路图
所谓电路图就是将电路工作原理用简单的符号标出来。
之所以要用到符号，因为不是人人都是艺术家，比如我画出一块电池，在我眼里是电池，但是在你眼里是砖头。所以我们在电路图中统一用各国(中国)制定的标准符号。
闭合电路
所有的电路都必须是一个闭合电路，也就是必须形成一个回路，让电流能进来能出去。即使在电路图中默认因为某个负载而导致电路开合，但是也应能够让其形成一个闭合电路，否则整个电路图都没有意义。
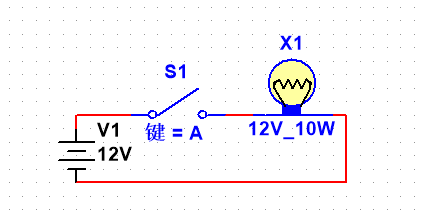
正确的闭合电路:
正确的闭合电路:(虽然初始时默认不是闭合，但是在之后仍然可以闭合的电路)
错误的电路
电路图中元器件的符号
具体的元器件符号可以自行在网络中搜索，这里就不在赘述了。
在查看符号时需要注意的是你当前查看的符号是哪个国家的标准。
线圈
顾名思义，线圈将是将导线缠绕成一个圈。
电容器
电容器类似于电池，它可以把电能暂时存储起来，同时具有放电的作用。
和电池不同的是，电容存电放电的效率比电池更高，相应的其容量一般不如电池。
欧姆定律
欧姆定律是电气电路中最基本的定律，虽然不是万能的但是使用广泛，公式为:
其中电流I与电压V成正比，电流I与电阻R成反比。
所谓的正比就是a大b变大，b大a变大，反比就是a小b变大，b大a变小。
另外我们只要得到电流，电压，电阻的任意两个数值就可以根据欧姆定律求出剩下的数值。
串联和并联
这个我们已经讲过很多遍了，不再重复。(主要是写吐了，看不懂的话去网上找别人的教程吧，串联并联在整个电路中都是十分重要的，不论是电气电路还是电子电路，所以不能不懂。)
直流电与交流电
电是我们看不见，不能随便摸的东西。我们想要直观的感受电长什么样子就需要通过波形图来观察。
通常我们使用"AC"来表示交流，使用"DC"来表示直流。
直流电波形:
交流电波形:
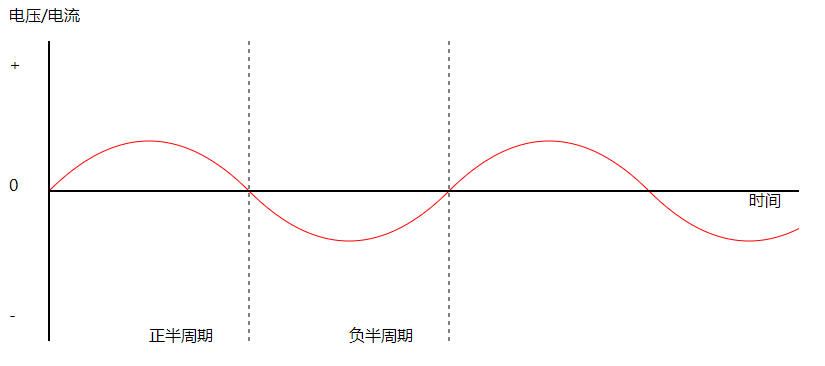
从图中可以看到交流电再正负周期反复循环，一个"完整周期"也就是正半周期加负半周期。
在进行到负半周期时，实际并不是电压或电流为负数，只有当其运动到0V时才是真正的没电。
在这里负号只是表明当前电流或电压的方向。也就是说当交流电电压为-220V时不是电压低于0的意思，而是当前电压与正常电压方向相反，其实质上还是220V电压，所以不要看到负数就以为没有电而去摸电线。
在区别交流电与直流电的符号时我们通常:
- 在描述直流电的符号时使用大写，如:V,R,A,I
- 在描述交流电的符号时使用小写，如:v,r,a,i
在家用小功率用电器中通常使用直流电，其电源插头一般内置将交流电转换为直流电同时降低电压的装置。即使是大功率用电器，如冰箱，洗衣机，也通常在机器内部将交流电分流出一部分转换为直流电以用来进行逻辑判断，达成某些设定。
交流电主要的用途是输电和作为能量供给。从波形图也可以看出来因为其没有直流电稳定，所以更方便变压器对交流电进行转换，更容易改变其电压。
三角函数
三角函数是分析交流电必不可缺的内容，在之前的学习中可能有一些人搞不懂sin，cos，tan都是什么东西，所以在这里我们重新学习一遍，我相信对于一个成年人来说这个东西并不会太难。
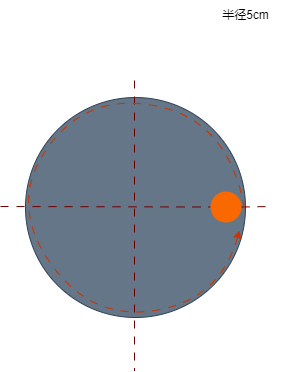
这个图中总共有两个圆，假设大圆的半径为5厘米。小圆会从上往下环绕大圆的边进行运动。小圆从起始位置运动一周后回到起始位置，这一过程需要360秒。
我们可以将其每秒的运动轨迹展绘制在图像中
可以看到，在这360秒中，当小球处在90秒时达到最高点，当运动到270秒时达到最低点。
其原理类似于下图
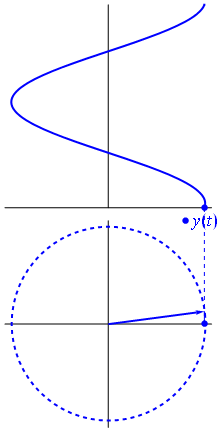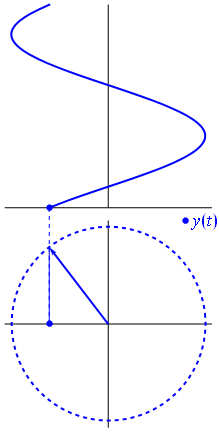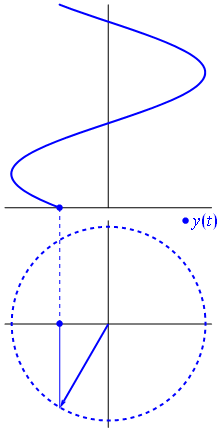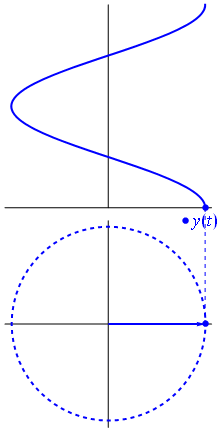
其实这就是三角函数sin的图像。
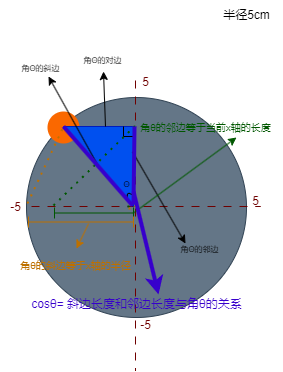
我们可以在大圆的圆周上的任意一点做一个直角三角形，这里我们假设小圆运动到这个位置，此时以小圆的位置也就是大圆的圆周上的一个点做一个直角三角形，如下图
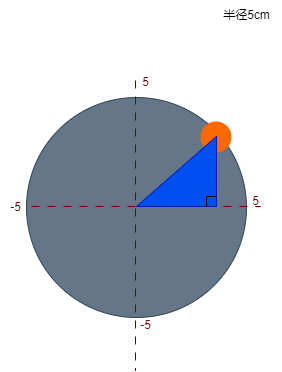
然后我们得到了角θ(读作"西塔")的对边，邻边与斜边。
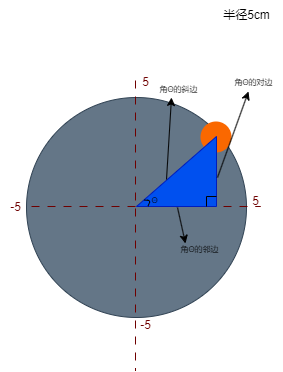
我们凭借肉眼观察这个直角三角形很容易发现，角θ的斜边长度就是大圆半径的长度，而角θ的对边长度就是当前小球在y轴上的位置.
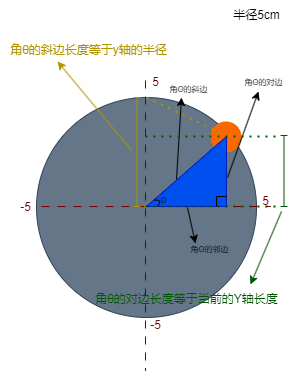
不管这个小圆运动到哪里，我们都可以做一个直角三角来算出他在y轴的位置。通常我们管这个直角三角形叫做"y轴的投影"。
在数学中我们使用"sinθ"来表达，所谓"sinθ"就是角θ和它的对边长度与斜边长度的关系。
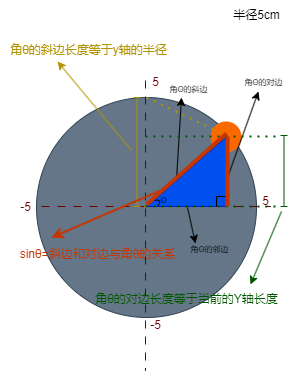
我们继续讨论小圆的运动，之前说小圆每360秒围绕大圆运动一周(也就是一圈)。
所以，当小园运动进行到43秒时，角θ的角度就应该是"43°"，进行到90秒时角θ的角度就是"90°"，也就是说时间的长短是可以与角θ的角度相互转换的。
时间与角θ转换就是依据角θ的对边长度来进行的
- 因为它的斜边代表的整个Y轴的半径，无论小圆在哪里，它的长度都不会改变。
- 而它的对边代表的是当前y轴的实时或者说是瞬时长度，也就是小园的圆心在y轴上的位置
所以sinθ的图像就像是交流电的图像
横轴即代表时间也代表度数，纵轴代表方向
- 当小圆运动为正时，代表他在大园的上半部分
- 为负时代表他在大圆的下半部分
- 当为0时说明小圆在大圆的正左或是正右端。
现在假设小圆运动到了这个位置，我们可以用cosθ来表示小圆的位置和半径的长度。在这个位置，我们可以看到一个新的直角三角形。
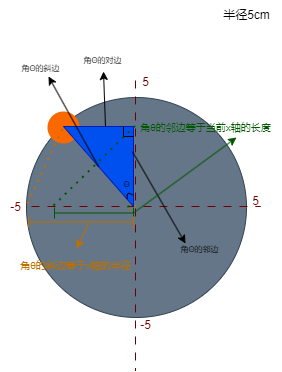
在这个直角三角形中，角θ的邻边长度就是当前小球在x轴上的位置。我们可以看到，无论小圆在哪里，它的斜边长度（也就是大圆的半径）都不会改变。而它的邻边代表的是当前x轴的实时或者说是瞬时长度，也就是小圆的圆心在x轴上的位置。
在数学中我们使用"cosθ"来表达，所谓"cosθ"就是角θ和它的邻边长度与斜边长度的关系。
所以，cosθ的图像就像是交流电的图像，只不过它表示的是小圆在x轴上的位置变化。
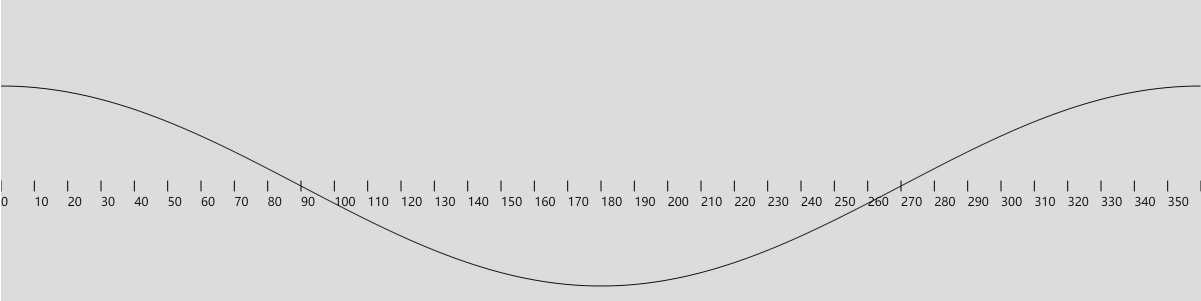
其与sinθ的波形图相同，区别是两者相差90°。因为cos以X轴为基准，而sin以y轴为基准，而x半径的角度与y半径的角度相差90°，所以使用cosθ和sinθ的表示方法也相差90°。
需要注意的是虽然两者表达含义相同，都可以表达出交流电的电流电压与其曲线变化，但是不要轻易的将两者混用。要么从开始到结束一直使用sinθ，要么一直使用cosθ，如果到了一定要混用的时候也要注意彼此的转换。
最后说一下斜边对边和邻边(底边)，再交流电中我们一般都是将直角三角形的锐角(也就是最长的边与第二长的边的角)作为θ角。
相应的θ角的对面就是对边，挨着θ角但是不与垂角相邻的角就是斜边(一般来说就是最长的那条)，挨着θ角同时挨着垂角同时不与斜边相接的就是底边(邻边)。
在描述时应该使用"谁的什么边"来描述比如"角θ的斜边"。因为每个角所对应的边都是不同的，如"垂角的对边"和"θ角的对边"所描述的不是一个东西。
