这一章是对02【基础电路】的补充,因为我觉得之前写的不是很好,所以补充了一下。在之后我也会补充其他章节,如果已经学会,可以跳过。
总电阻
所谓总电阻,就是指某个电路中所有电阻的总值。
在串联电路中计算总电阻十分简单,因为在串联电路中电流相等,所以串联电路的总电流就是串联电路的电流;我们只需要用欧姆定律求出每个负载的电阻然后将其相加,得到的和就是总电阻。
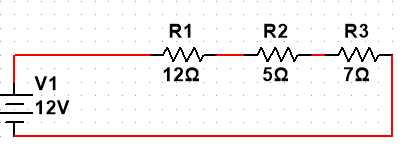
上图是一个串联电路,因为其负载本身就是个电阻元件,所以就不需要计算负载的阻值,我们如果想要计算其总电阻只需要使用如下公式:
所以上图电路中其总电阻为
但是当我们想要计算并联电路中的总电阻时就没有这么简单了,因为在并联电路中电压相同,电流不同。所以并联电路的电压就是总电压,我们需要分别求出每条支路的电流,之后计算总电流,最后使用欧姆定律得到总电阻
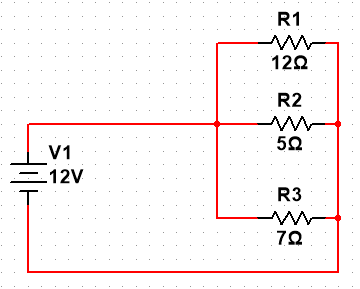
- 首先我们要计算其总电流,根据欧姆定律电流的公式为
- 也就是说:
- 我们把所有支路的电流相加,得到的和就是总电流:
- 由于总电压V在并联电路中即是电源电压,不会变动。所以我们可以简化公式,将V提出来:
- 之后我们可以假设
- 而因为这两个公式都是等于总电流的意思,我们可以让这两个公式相等:
- 因为这个等式的两边都有总电压V,而总电压不可能为0,否则也就没有电,所以我们可以使用数学中的运算规则"当等式的两边都有相同的非零因子时,我们可以将它们约去"。所谓的约去就是"约除公因子",当我们约除公因子时本质上是进行这样的运算:
- 之后我们将V消除,得到如下公式:
如此一来我们便可以使用这个公式来计算并联电路中的总电阻了,让我们实际应用一下
- 在上图的并联电路中总电阻为:
- 然后我们取0.426的倒数:
所以在上图中并联电路的总电阻为
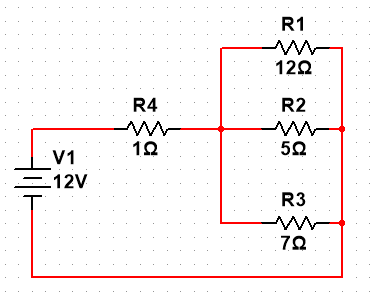
如果我们要计算下图中这种串并联混合的电路总阻值,首先计算并联的R1、R2、R3的总阻值,最后将总阻值加上R4即可。
等效电路
等效电路就像是一个电路的"化身"或者说是"替身",当我们面对复杂的电路时,有些地方可能让我们一头雾水、难以理解。这时我们就可以设计或是找到一个等效电路,让他在某些方面的表现和复杂电路一样。这个简单的电路就是等效电路。
举个例子,假如我们在看一部动作电影,当面对一些危险的动作和场景时,导演为了保护演员会请专业的替身来完成这个动作。这个替身就像是演员的等效电路,演员和替身在荧幕中的动作、服饰、样貌是一样的,但是他们的生活经历,真实的身份却完全不同。
之前我们在计算并联电路时假设的
基尔霍夫定律
基尔霍夫定律是用来计算电路中各种值的定律,它可以计算任何电路,无论是串联并联。
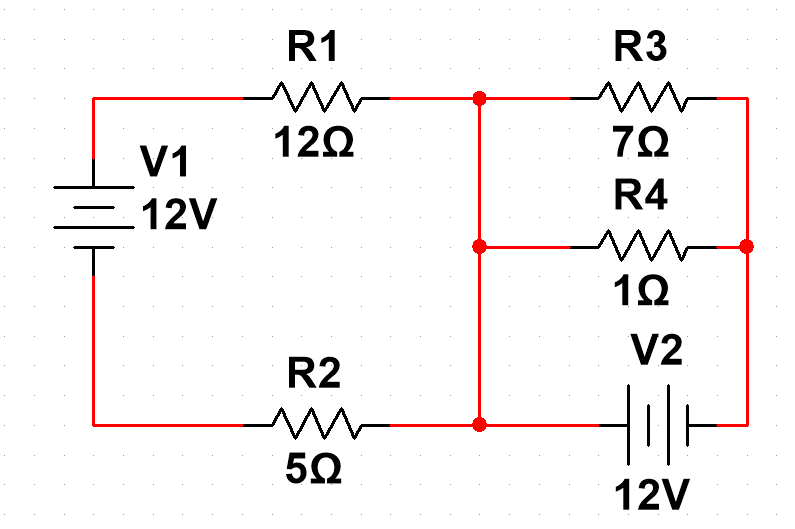
想要求出这个电路的电流电压我们首先需要明白基尔霍夫定律的两条定律:
- 电流保存定律:在任一瞬时,流入电路中任意接点的电流的和等于流出该接点的电流的和。
- 电压下降定律:闭合电路中的电动势之和等于负载处被消耗的电压和。
所谓电动势就是电源将其他形式的能量转换为电能的能力。比如我们图中的电池拥有化学能转变为电能的能力,风力发电机有把风能转换为电能的能力,发电厂的交流发电机有把磁能和机械能转换为电能的能力,这个转换能量的效率就叫电动势。通常来说我们电路的电动势本身就是电源提供的,不需要我们单独的计算其电动势,此处关于"电压下降定律"我们只需要明白电动势为何物就好。
接下来如果我们要计算上面电路的电流电压,首先我们要知道这条电路电流的走向和接点。
- 所谓接点即导线和导线之间连接的点
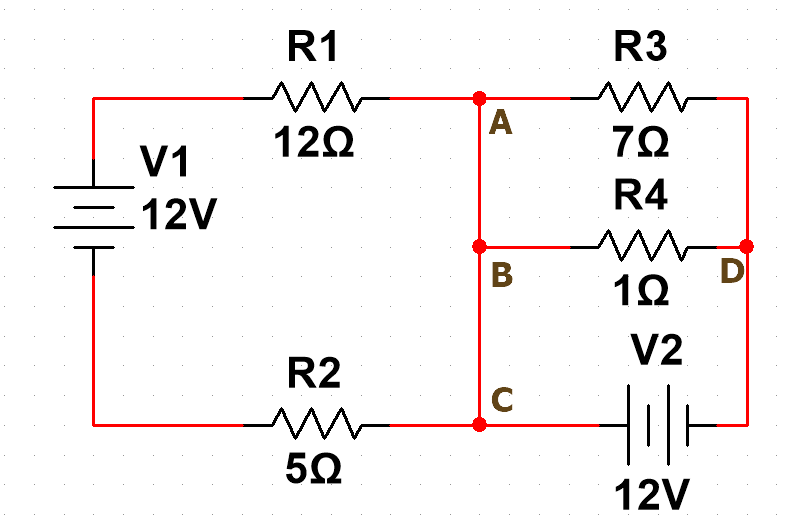
如上图所示,在此电路中一共有abcd四个接点,而电流的走向也显而易见:
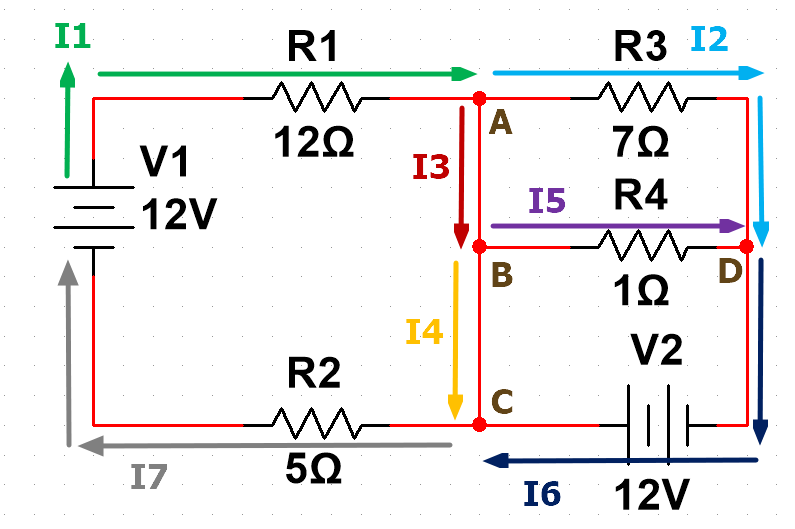
接下来我们使用"电流保存定律"计算各个接点的电流
- A接点的电流:
- B接点的电流:
- C接点的电流:
- D接点的电流:
之后我们使用"电压下降定律"来计算电压,我们首先观察左侧的这个回路:
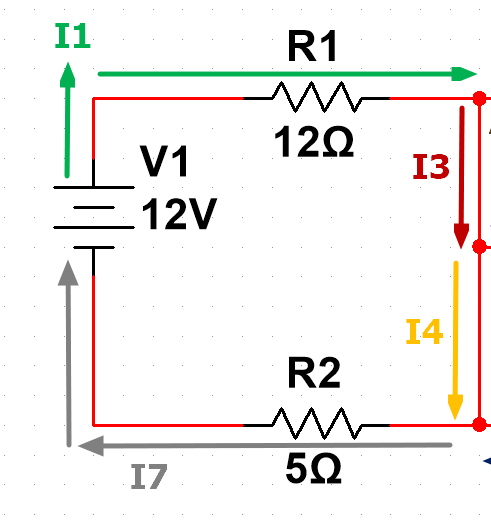
这个回路中共有两个负载,分别是R1和R2,所以流经的电流就分别是I1和I7。之后我们根据欧姆定律电压计算公式即可计算出左侧回路的电压。
- 欧姆定律电压公式 :
- 所以
让我们来实际试一试
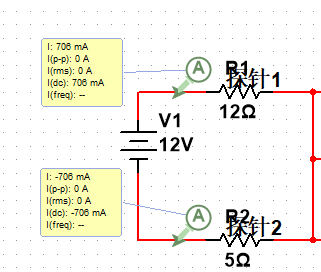
这里我们就不在计算电流的数值了直接使用探针,得知I1=0.706A,I7=-0.706A。
当我们想要计算电流和电压的大小时,可以忽略其负号,因为正负只是代表方向。
- 所以V1回路的电压为:
这个结果与我们的电源电压基本吻合,右侧电路同理,这里便不再重复了,不妨自己动手试试。
这里提醒一下,欧姆定律计算电流的公式:
在我们这个电路中V就是电源电压。而右侧是一个并联电路,所以计算电压时只需计算一条支路即可。
这一章我们学到了什么?
- 总电阻
- 等效电路
- 基尔霍夫定律



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 没有源码,如何修改代码逻辑?
· PowerShell开发游戏 · 打蜜蜂
· 在鹅厂做java开发是什么体验
· WPF到Web的无缝过渡:英雄联盟客户端的OpenSilver迁移实战