三相电与星、三角接法
三相电是一种依托于交流电的技术，它可以使电力的传输与转换更加的高效、安全。在生产环境中，三相电多用于工业设备与输电网络。
三相电的原理
要了解三相电的原理我们首先要知道发电厂是如何生产电力的。我们以基本交流发电原理为例:
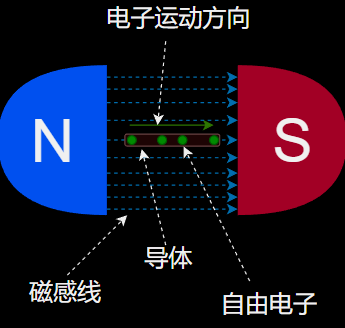
当磁铁的N极与S极相对时产生磁场，磁场驱动自由电子在导体中流动，这一过程叫做电流。而电子在导体中流动的这一过程被叫做电流。也就是说电流的大小与磁场的强弱密不可分，而电子的移动方向受到磁感线的影响。
在图中磁感线从N极发出，影响导体的左侧，导体左侧的电子被磁场影响垂直于磁感线的平面移动，在图中变现为向右移动。此时磁场越强，电压也就越大，进而电流也就越大。随着导体的方向不断变化，电子受到磁场的影响也会发生变化。
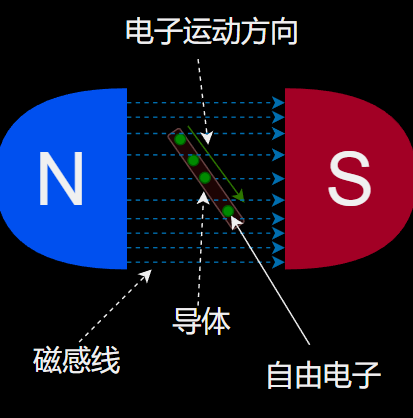
当导体旋转时，由于磁场的影响，电子的移动方向发生变化
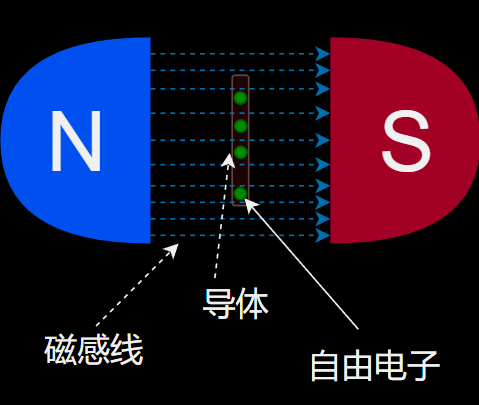
当导体旋转至此时，由于导体内部没有足够让电子流动的空间，遂电子无法被磁感线影响而移动，此时电压电流均处于或是趋近于0V。
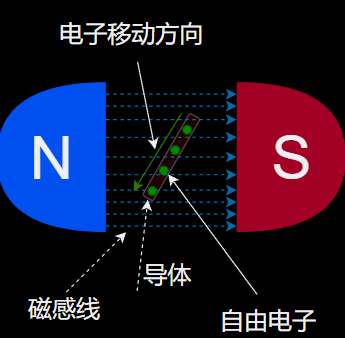
当导体继续旋转，电子方向再次改变，受到磁场的影响也会越来越大，也就是说电压会逐渐升高
如此循环往复，直至旋转360°也就是一圈，我们称其为一个“周期”
在下面的波形图中可以更直观的感受到,在第一章我们也讲过。
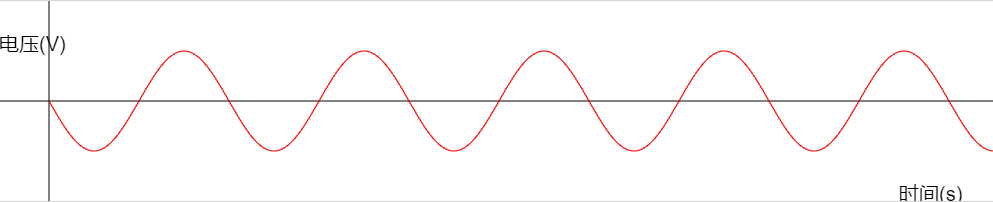
这种普通的交流电我们称之为单相交流电，观察波形图我们可以发现在交流电运行一个周期时会经过电压为0V的位置，所以造成了一种每进行半个周期时电力就会暂时中断。
所谓的三相交流电即将磁场的线圈或是导体呈120°分割成三份，这样在旋转导体时就可以让磁场无死角的驱动电子进行运动，便不会造成电力短暂中断，如图所示:
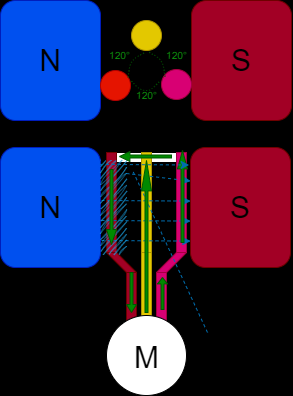
这是一个简易的三相电原理，当磁场影响红色导体时，导体内部电子流动，当经过负载(此处M为电动机)后电流从黄粉两个导体返回，因为负载会起到限制电流的作用所以不会造成短路。
也因此，黄粉两条路线的电流与红色路线的电流方向相反(+-符号相反)，同时红色导体的电流是其他两路导体的电流之和。之后我们将称呼每条路线为“相位”
我们还是那上面图举例子，当红色相位的电流为5A时，那么其他两路就是-2.5A。我们来试验一下
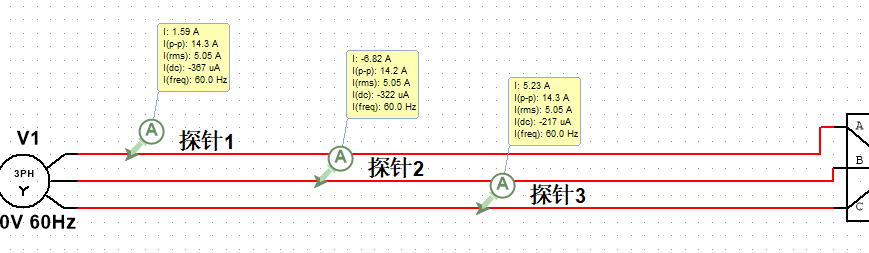
可以看到
- 探针1所在的相位电流1.59A等于其他两个相位的和\((-6.82+5.23)=-1.59\),最后将结果的符号取反便得到了1.59A，其他的相位同理
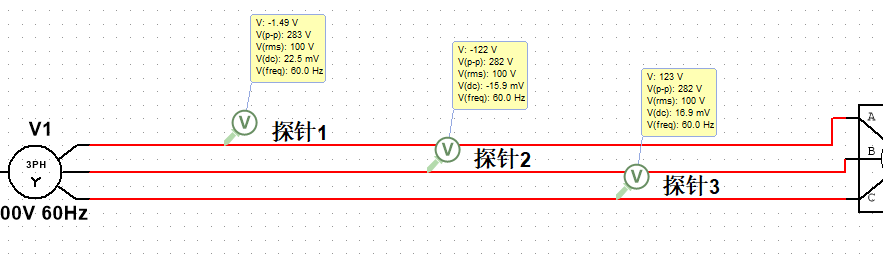
我们发现瞬时电压，也就是实时电压也可以得出这个规律。
通过观察三相电的波形图我们就可以更直观的看出，在一个三相电系统中任意一个相位的电压等于其他两个电压的和，如图中所示：
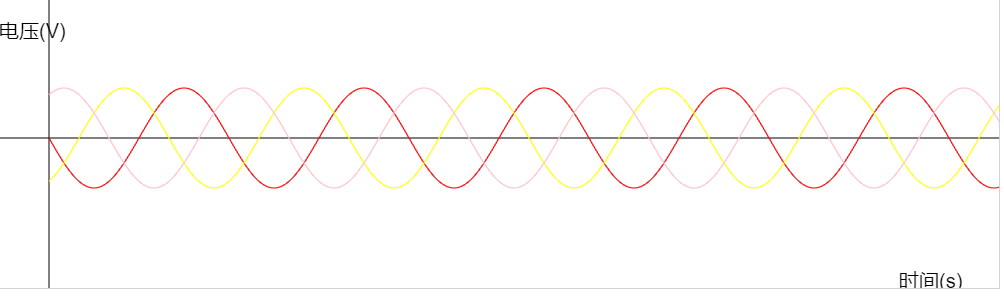
- 当粉色相位处于0V时，其他相位处于最顶和最底端。\(最顶端电压+最底端电压=0V\)
- 当粉色相位处于最顶端时，其他相位处于最底端。\(最底端电压+最底端电压=最底端电压(符号取反)\)
相量
相量:我们需要经常处理一些既表示方向同时又有大小的量，比如电压电流的方向和大小，这些都可以使用相量表示。相量是一个二维坐标，他们可以用箭头来表示，箭头的长度代表单位的大小，箭头的方向代表不同的相位。
相位:在交流电路中，电压和电流随着时间进行变化，不同线路的电压电流他们之间的峰值不一定会在同一时间达到其峰值。这种时间上的差异就叫做“相位差”，在相量中，我们可以用角度的方法将表示相位，比如0°，90°，-90°等等。
相量图我们可以在2维的平面坐标系中画出相量，横轴正半轴对应0°，逆时针旋转角度增大，顺时针旋转角度减小。例如，纵轴正半轴对应90°，纵轴负半轴对应-90°。在我们所要学习的三相交流电系统中，可以把相量看作是一个导线，然后我们把这个导线切开观察其横截面，便可以观察到三相中每一相的电压或是电流是如何变化的。即使这三相的电流或是电压都在一根导线上但也不会出现短路或是其他问题，因为这根导线是我们幻想的、虚构的、抽象的一根东西，其本质是抽象出来的三相交流电系统的模型。
警告:(在现实中三相电每一相都是独立的火线，不要将三相并到一根导线上,这会造成短路发生爆炸。我举得例子只是方便理解)
相量的大小：在相量图箭头的长度代表单位的大小，箭头的方向代表不同的相位。假如两个相位的长度相等，那么其大小就相等
在理想中的三相电其输出应该是稳定、对称的。如波形图所示
- 每一相的幅值相等(也就是电压大小相等)
- 频率相同（每一相在一秒内运动的完整周期次数相同）
- 初相角之间依次相差应为120°
- 你可以把三相电想象成一个跑步比赛。假设有三个跑步者A、B和C，他们在同一条跑道上跑步，但是他们的起跑线并不在同一个地方。A跑步者的起跑线在跑道的起点，B跑步者的起跑线在跑道的1/3处，C跑步者的起跑线在跑道的2/3处。也就是说，他们的起跑线之间相差了跑道长度的1/3，这就像是120°（因为360°/3=120°）
- 当比赛开始时，A跑步者从起点开始跑，B跑步者和C跑步者也同时开始跑，但是他们的起跑线并不在同一个地方。这就像是三相电中的每一相在时间t=0时的状态，也就是它们的"初相角"
- 所以，"初相角之间依次相差120°"就像是跑步者A、B和C的起跑线之间相差了跑道长度的1/3。这就是为什么我们说在三相电中，每个相位的初相角是依次相差120°。
在三相电路中，从电源到负载之间每一相位的电压被称为相电压，如图所示:
图中每一相的电压被称为相电压，如A相的相电压就是指橙色范围内的电压，而流经每一相位的电流也就是相电流，如A相的相电流同样指橙色范围内的电流。此外我们更习惯称呼三相为“U,V,W”而不是"A,B,C"（当然这个全凭个人喜好，只需要知道U、V、W是什么东西就好，不要与其他单位混淆）
在相量图中相电压可以如下图表示：
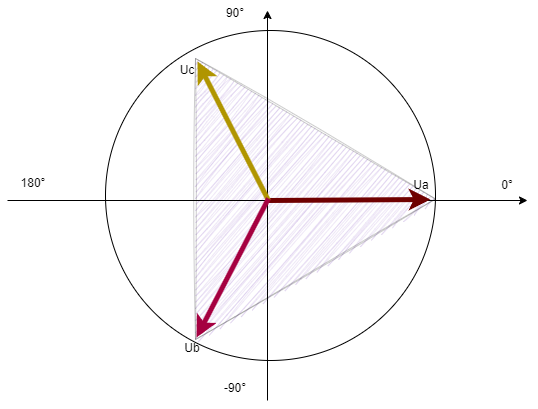
- Ua即a相位的相电压
- Ub即b相位的相电压
- Uc即c相位的相电压
- 每个相位的长度相同即表示它们相电压大小相同，例如220V的相电压就是长度均为220个单位
我们现在知道了何为相电压，在进一步学习线电压之前我们需要了解一下“星形接法与三角形接法”
星形接法如下图所示：
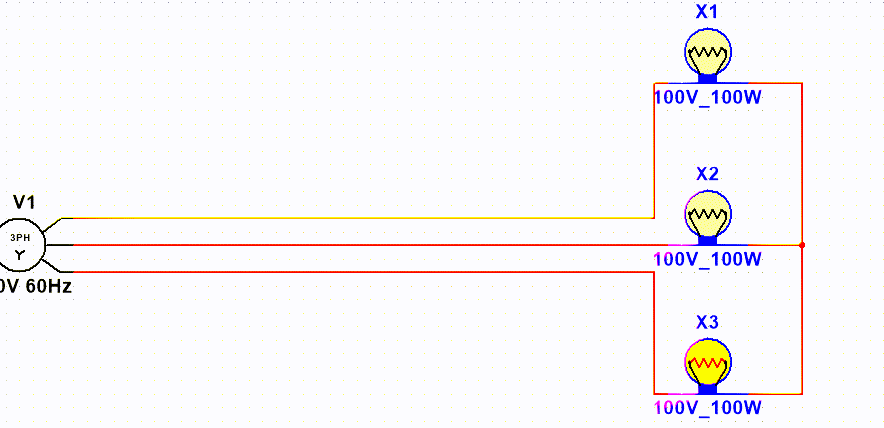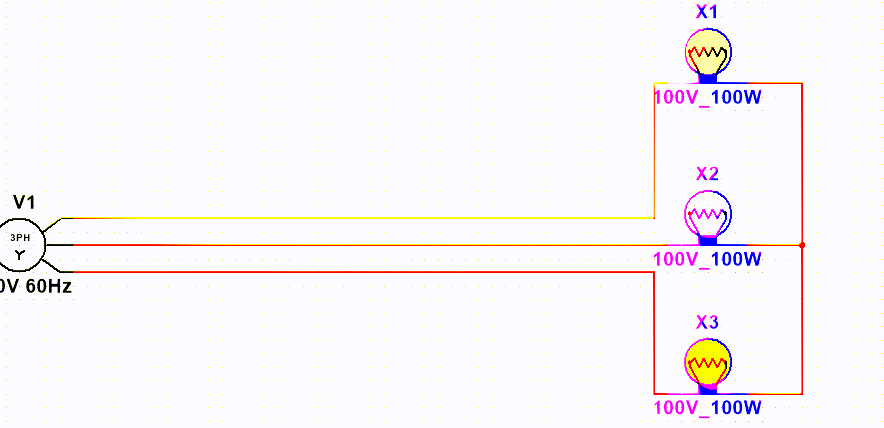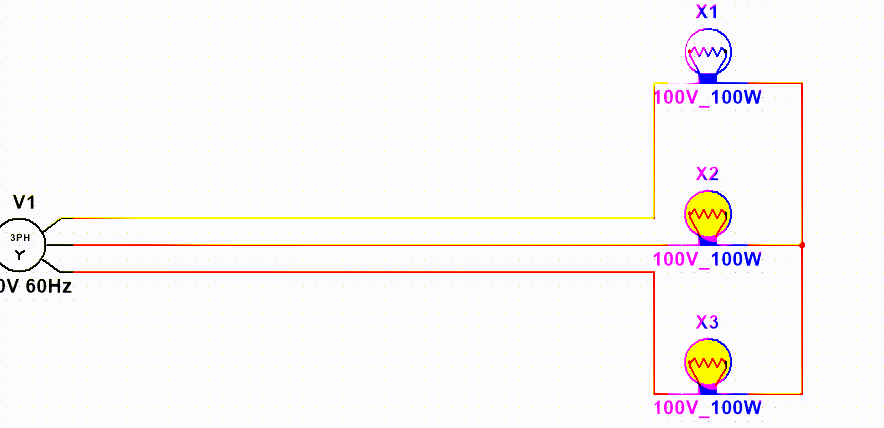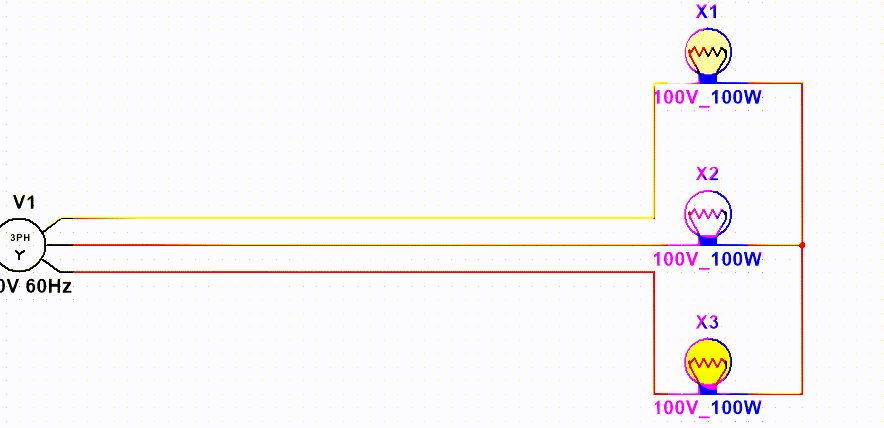
可以看到星形就是将三个线的输出端连接在一起，形成一个"星点"或者叫做"中性点"，用“N”表示，这样我们就不在需要连接零线。(在三相四线制中仍然需要接零，所谓三相四线制就是3根相线一根零线的电路)。
之所以不再需要零线是因为每个相位的瞬时(实时)电压或是电流都是其他相位之和，也就是说当A相线的电压1V时，其他两相就是-0.5,所以我们将A相和其他两个相线连接在一起时他们就会抵消"\(1+(-0.5)+(-0.5)=0\)",如此一来这个中性点就一直是0V,我们也就没必要再接一根零线，而是把这个点当作零线。
但是既然不需要零线，为什么又有“三相四线制”这个东西呢？答案很简单，在三相电系统中，每一条相线的电压电流都是独立的。当每条相线连接的负载功率或电阻不同时便会影响相线的电压或电流，这样就会导致三个相线的相电压与相电流不平衡，此时再将他们的一端汇聚到中性点时，中性点就会过热或是短路或是发生其他诡异的事情，总是就是不稳定的、危险的。所以当采用星形接法时必须保证三相平衡。如下图所示:
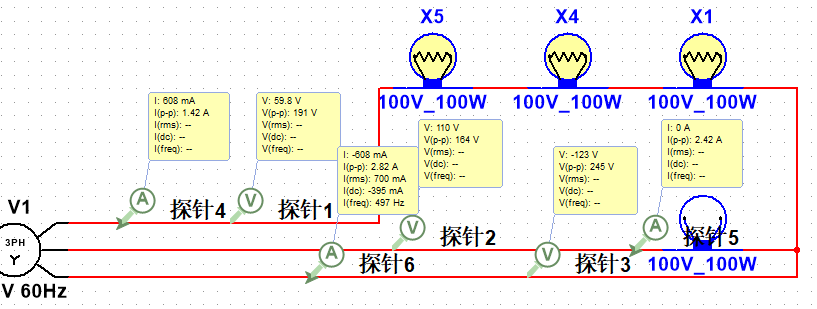
此时这个三相电路的平衡被破坏，我们之前所得出的规律“任意一相的瞬时电流或瞬时电压等于其他相的瞬时电流或瞬时电压之和”，也被破坏，因此就会出现各种问题，比如我们的B（第二个）相位电压变成了110V,导致灯泡损坏。要解决这个问题我们只得引入一根零线，也就是三相四线制来解决这个问题。
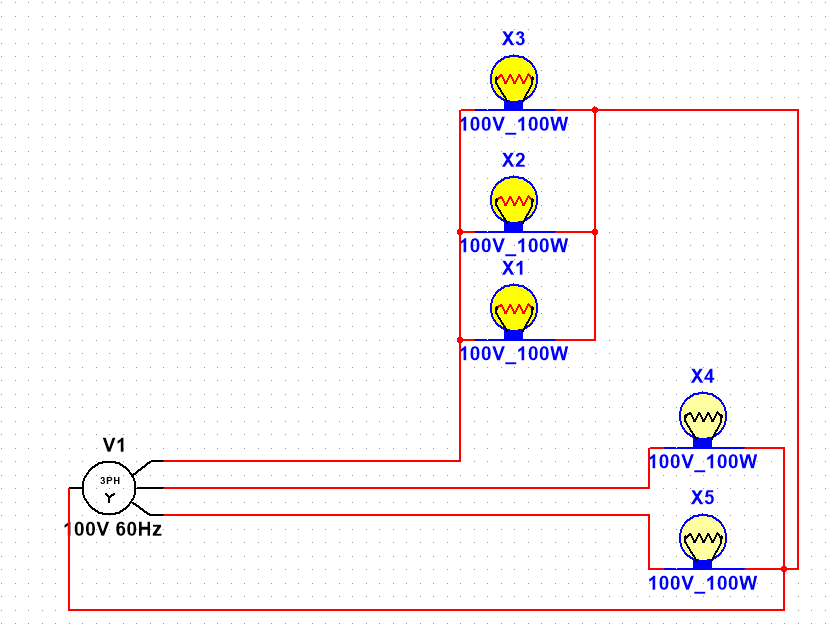
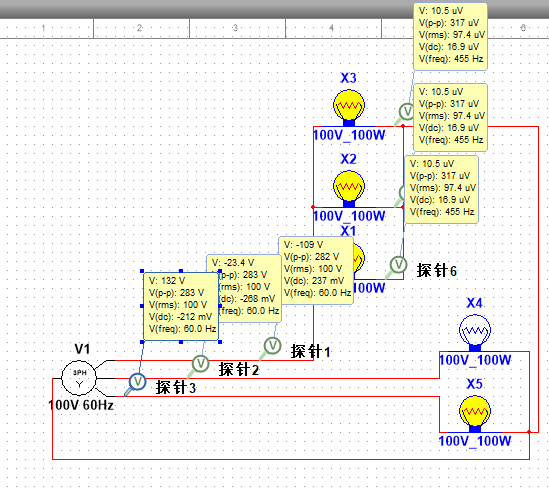
我们这里在A相采用了并联的方案，因为我们实验的三相电源只有100V，所以我们采用并联让每个支路的电压相等，这样A相就可以让三个灯泡正常运行了。此时的A相的相电压就是A的主路电压，具体可参考上一期的串联与并联。
三角形接法如下图所示:
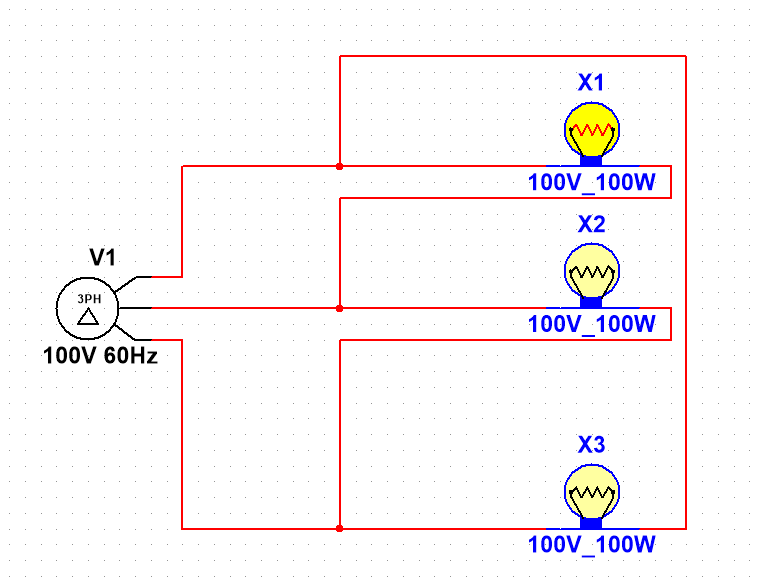
即A相尾端接B相首端，B相尾端接C相首端，C相尾端接A相首端，简而言之就是三个相首尾相连。
线电压与线电流的概念。
线电压即是各个导线的线端之间的电压，所谓线端就是一条电线的出口和入口，在我们这个三角形接法电路中，各相线端如下:
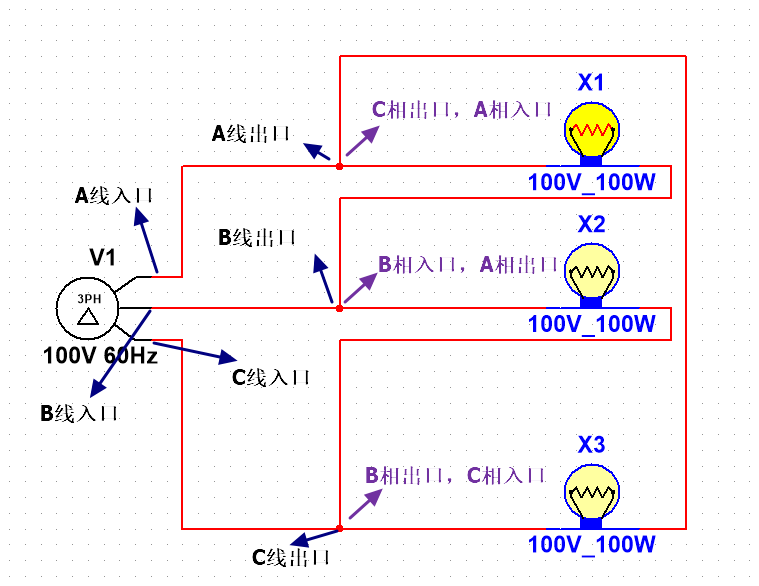
在了解线端后我们就很容易找到线电压的关系了，之前说线电压是各个导线的线段之间的电压，如下图示:
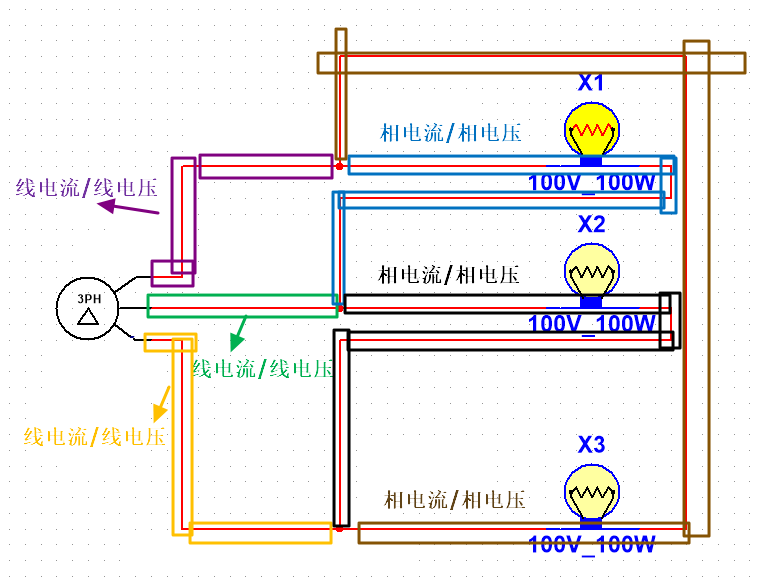
看到这个图就很容理解，在三角形接法中相电压等于线电压的意思，因为三角形的接法类似于并联电路，电压处处相等，所以相电压和线电压没有区别，前提是三相平衡。
而线相电流在三角形接法中则不同，
所谓线电流就是流经导线的电流。
星形接法的相电流由于每根相线均为独立的所以每根相线的电流取决于其负载和串并联的连接。又由于星形接法的每一相的负载都直接连接到相应的相线上，所以在星形接法中线电流就等于相电流
三角形接法中，相电压等于线电压，但是相电流不等于相电流。在三角形接法中线电流的计算原理与我们下边的在相量图求星形接法的线电压原理相同，这里便不再重复了。简而言之，在三角形接法中"线电流是相电流的\(\sqrt{3}\)倍"，即
- 举个例子，我们可以看到A相线的电流从A相线的入口进入，再从A相线的出口流出。
- 这时，B火线的线电流从B相线的入口进入，刚好遇到从A相线出口流出的电流。
- 此时就会导致A的相电流与B的线电流产生叠加，而由于A的相电流经过了负载产生了损耗，所以A的相电流比B的线电流小。
- 同理，A线电流与C相电流叠加，A的线电流发现变化，C的线电流与相电流叠加，C的线电流发生变化
- 之后我们如果要计算其线电流，那么就需要将"相电流*\(\sqrt{3}\)",这个公式作用就时得出抵消之后的线电流
- 至于为什么是\(\sqrt{3}\)，可以查看下面用相量图求星形接法的线电压方法，其原理与此相同，只需要把相电压箭头换成相电流箭头,Uab换成Iab即可。
了解了线电压/线电流的范围我们就可以计算线电压的数值
- 在三角形接法中，线电压的计算公式为
- 也就是说在三角形接法中线电压等于相电压
我们可以在相量图中表示星形接法的线电压：
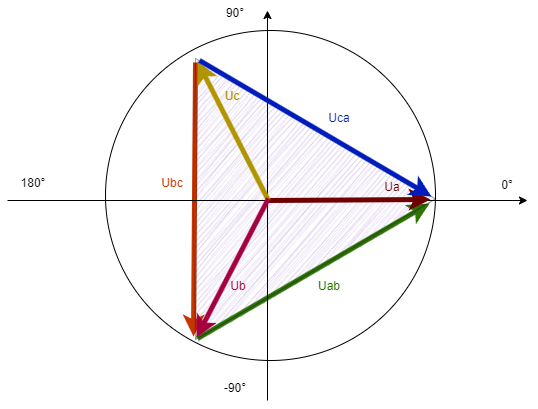
在相量图中想要求Uab的线电压就是Ua-Ub，两个相量的相减就相当于他们的箭头相连接，箭头的指向“被减数”，这里的被减数就是“Ua-Ub”中的Ua,所以我们的Uab线电压相量的箭头就指向a。
现在我们可以根据这张相量图来计算星形接法的线电压
首先我们知道在相量图中Uab的夹角是120°，因为在三相电中初相角必须是120°，这是由交流三相电发动机的设计所决定的，否则会导致三相不平衡。
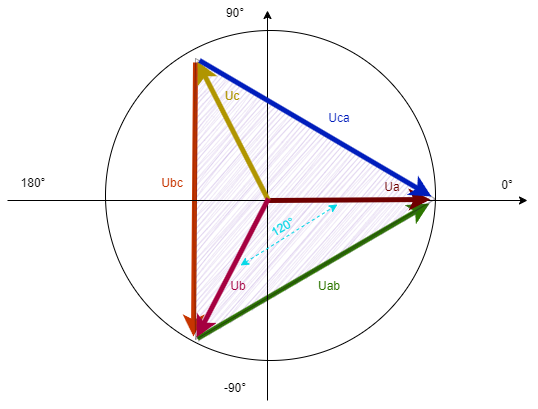
然后我们得到了得到了三个顶点Ua,Ub,原点，以此可以组成一个等腰三角形，随后我们画出这个等腰三角形的高，这个高可以充当我们得到的等腰三角形的对称轴，根据这个对称轴可以再次把得到的等腰三角形分割为两个直角三角形。
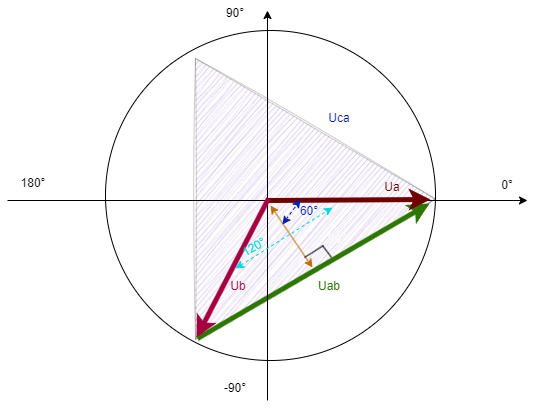
我们接下来只需要求出顶点Ua到垂点(90°的那个点)的长度，然后乘以2就可以得到整个Uab线电压相量的长度。
- 目前已知，原点到Ua的边为100(也就是相电压ua)，等腰三角形的对称轴到ua的角度为60°，所以我们可以根据三角函数求出垂点到ua的长度
- 所以\(垂点到Ua的长度 = 100*sin(60°)=86.6\)
- 也可以把\(sin(60°)\)写成\(\frac{\sqrt{3}}{2}\),他们是一个意思
- 最后我们把这个长度乘2就是173.2V，这就是Uab的长度也就是Uab线电压的大小
- 最后我们得出一个计算星形接法的线电压的公式，即"\(相电压*(sin(60)*2)\)"或"\(相电压*\sqrt{3}\)"
我们依靠相量了解了相电压、相电流、线电压、线电流的关系与计算方法，不得不感叹数学的神奇。最后让我们做个总结：
- 星形接法中线电压等于相电压*根号3，线电流等于相电流
- 三角形接法中线电压等于相电压，线电流等于相电流*根号3
- 使用相量图表示相电压、相电流、线电压、线电流时，箭头便是他们的方向，长度表示他们的大小，相量与相量之间的角度我们称之为相角表示其正弦的角度，或者说是在波形图中周期运动变化的角度。
- 使用相量计算线电流与线电压时，使用对称轴或者是平分线将等腰三角形分割为两个直角三角形，根据斜边(也就是直角三角形垂点对面的边，一般是相电压或是相电流)使用三角函数来计算出线电流或线电压的大小，之后将两个直角三角形合并回一个等腰三角形，也就是将得到的线电流、线电压的长度*2，最后便得到了线电流、线电压。
- 无论哪种接法在三相电路中都必须保持三相平衡，一旦三相平衡被破坏就会破坏整个三相电系统的稳定，进而引起故障甚至事故。
在这一章我们可以学到什么？
- 三相电的原理
- 相电压与线电压
- 相电流与线电流
- 相量和相位与相量图
- 星形接法和三角形接法
- 三相电路的平衡
