数据结构学习笔记(一)--时间复杂度

数据结构学习笔记(一)--时间复杂度

时间复杂度章节简单，所以并不详细讲述。

时间复杂度的定义

事先预估算法时间开销 T(n) 与问题规模 n 的关系(T表示"Time")。

时间复杂度的具体计算

用c语言代码举例：

//算法1—— 逐步递增型爱你
void loveYou(int n){ //n为问题规模
    //语句1
    int i = 1; //爱你的程度
    //语句2
    while(i<=n){
        //语句3
        i++;
        //语句4
        printf("I Love You %d\n",i);
    }
    //语句5
    printf("I Love You More Than %d\n",n);
}

语句频度：

1. 一次
2. 3001次
3. 3000次
4. 3000次
5. 1次

时间开销与问题规模n的关系为：

T(n) = 3n+3

即每行代码执行一次便加1

时间复杂度通用计算

一个算法的时间开销表达式可以只需考虑阶数高的部分(高阶部分的系数也化为1)，只需考虑循环内的一个基本操作分析他的执行次数和问题规模n的关系。

例如：

T(n) = 3n+3; T(n) = O(n)

T(n) = n²+3n+10000; T(n) = O(n²)

加法规则

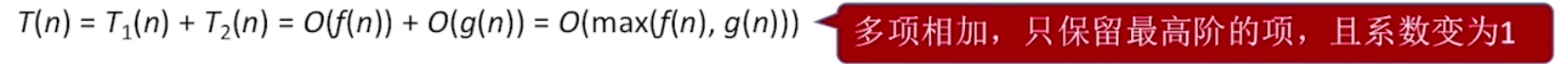
乘法规则

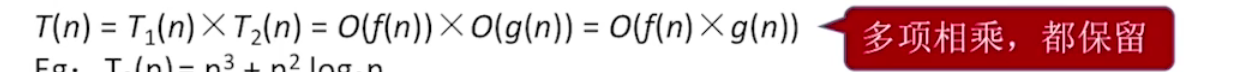
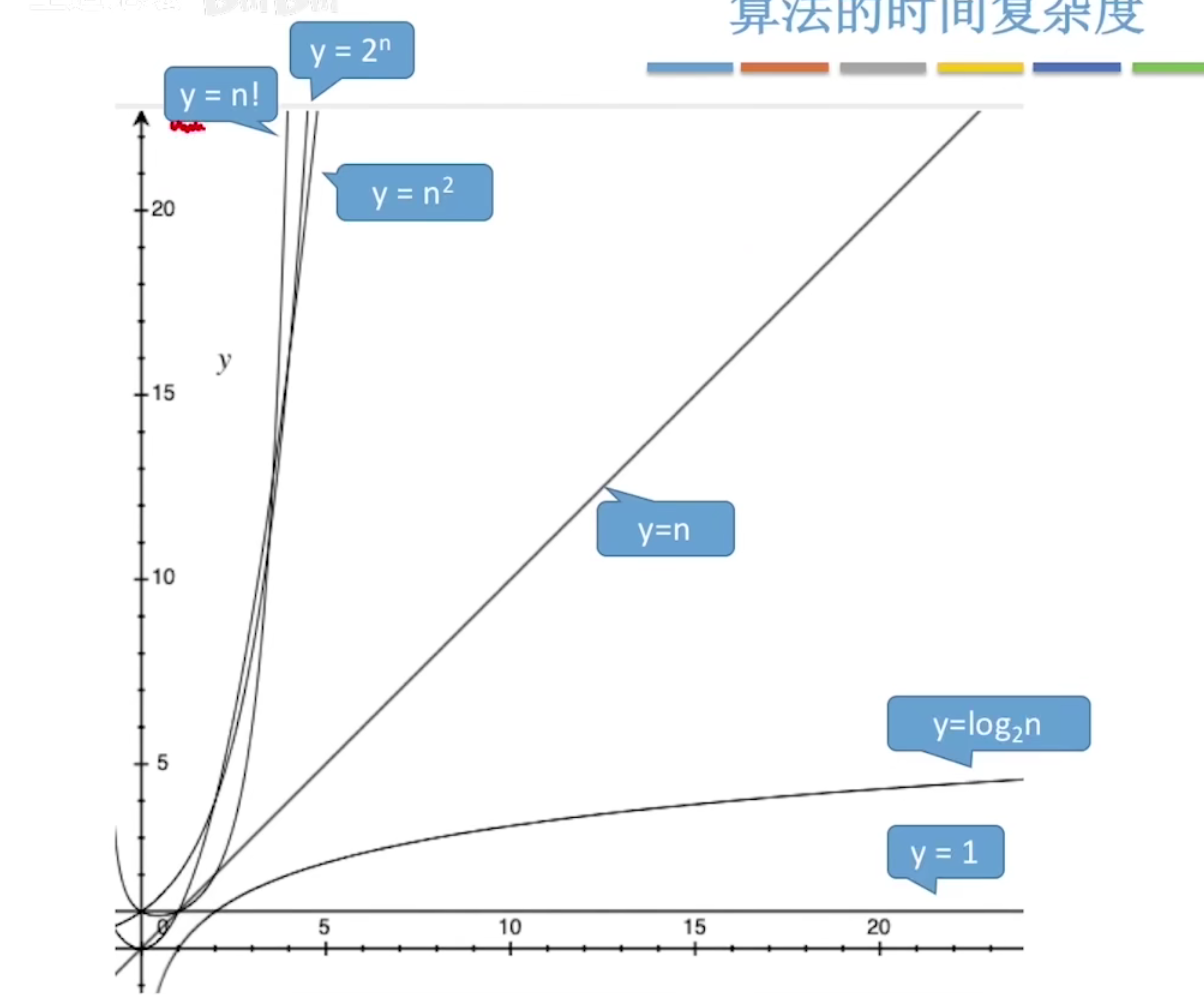
时间复杂度的大小排序

从小到大排序

口诀：常对幂指阶

图形显示

嵌套循环的时间复杂度

利用加法规则与乘法规则，用c语言代码举例：

//算法2—— 嵌套循环型爱你
void loveYou(int n){ //n为问题规模
    int i = 1; //爱你的程度
    //外层循环执行n次
    while(i<=n){
        i++; //每次+1
        printf("I Love You %d\n",i);
        //嵌套两层循环
        for(int j=1;j<=n;j++){
            //内层循环共执行n²次
            printf("I am Iron Man\n");
        }
    }
    //语句5
    printf("I Love You More Than %d\n",n);
}

时间开销与问题规模n的关系：

T(n) = O(n) + O(n²) = O(n²)

结论: 如有多层嵌套循环，只需考虑最深层循环的循环次数与n的关系

分情况讨论时间复杂度

讨论最好情况，最坏情况与平均情况的时间复杂度，一般只考虑最坏时间复杂度与平均时间复杂度。

用c语言代码举例:

//算法4—— 搜索数字型爱你
void loveYou(int flag[],int n){ //flag数组中乱序存放了1~n这些数字，n为问题规模
    printf("I Am Iron Man\n");
    for(int i=0;i<n;i++){//从第一个元素开始查找
        if(flag[i]==n){//找到元素n
            printf("I Love You %d\n",n);
            break;//找到后立即跳出循环
        }
    }
}

计算上述算法的时间复杂度T(n)

• 最好情况：元素n在第一个位置 ---最好时间复杂度 T(n) = O(1)
• 最坏情况：元素n在最后一个位置 ---最坏时间复杂度 T(n) = O(n)
• 平均情况：假设元素n在任意一个位置的概率相同为1/n ---平均时间复杂度T(n) = (1+2+3+...+n)(1/n) = (1+n)/2 =O(n)

---

点击进入下一篇:数据结构学习笔记(二)--空间复杂度