什么是梯度
【直观理解!】什么是梯度?博士带你快速啃透神经网络核心概念“梯度”!一个视频讲明白!-人工智能/损失函数/偏微分/激活函数/感知机_哔哩哔哩_bilibili
回归就是根据已有的数据的分布建立神经网络的模型,去预测未知的数据。分类就是希望用一条直线或者曲线将已知的数据分成两类或者多类。
所谓梯度下降就是沿着梯度所指出的方向一步一步向下走找出损失函数最小值的过程。
梯度就是函数在某个方向上的导数。
函数有多少个自变量,它就有多少个偏微分。

梯度是函数在所有自变量方向上的偏微分所组成的一个向量。向量的方向是梯度的方向向量的模是梯度的大小。
偏微分是在某个特定方向上的导数,它是一个标量。只有大小没有方向
梯度它是一个向量不是一个标量。
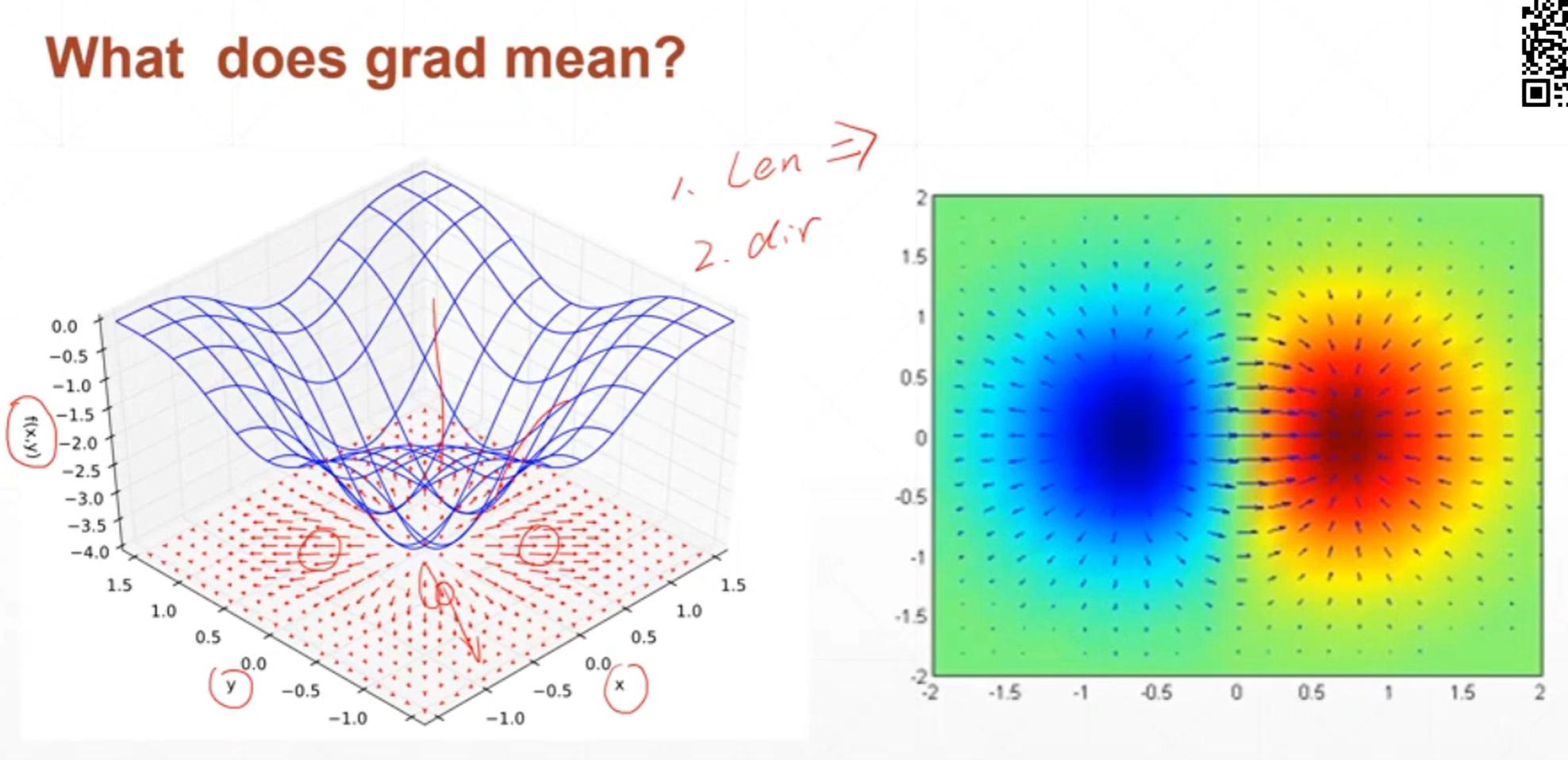
梯度的长度反映了函数曲面的变化的剧烈程度,梯度的值越大说明函数曲面越陡峭,梯度的值越小说明函数曲面越平缓。
梯度是一个向量,方向代表了函数在这个方向上增长的方向

我们初始化的值就是这个函数的局部极小值,在这个局部极小值上梯度不会得到更新,但此时在此处已经是函数的极小值了,这只是一个巧合。
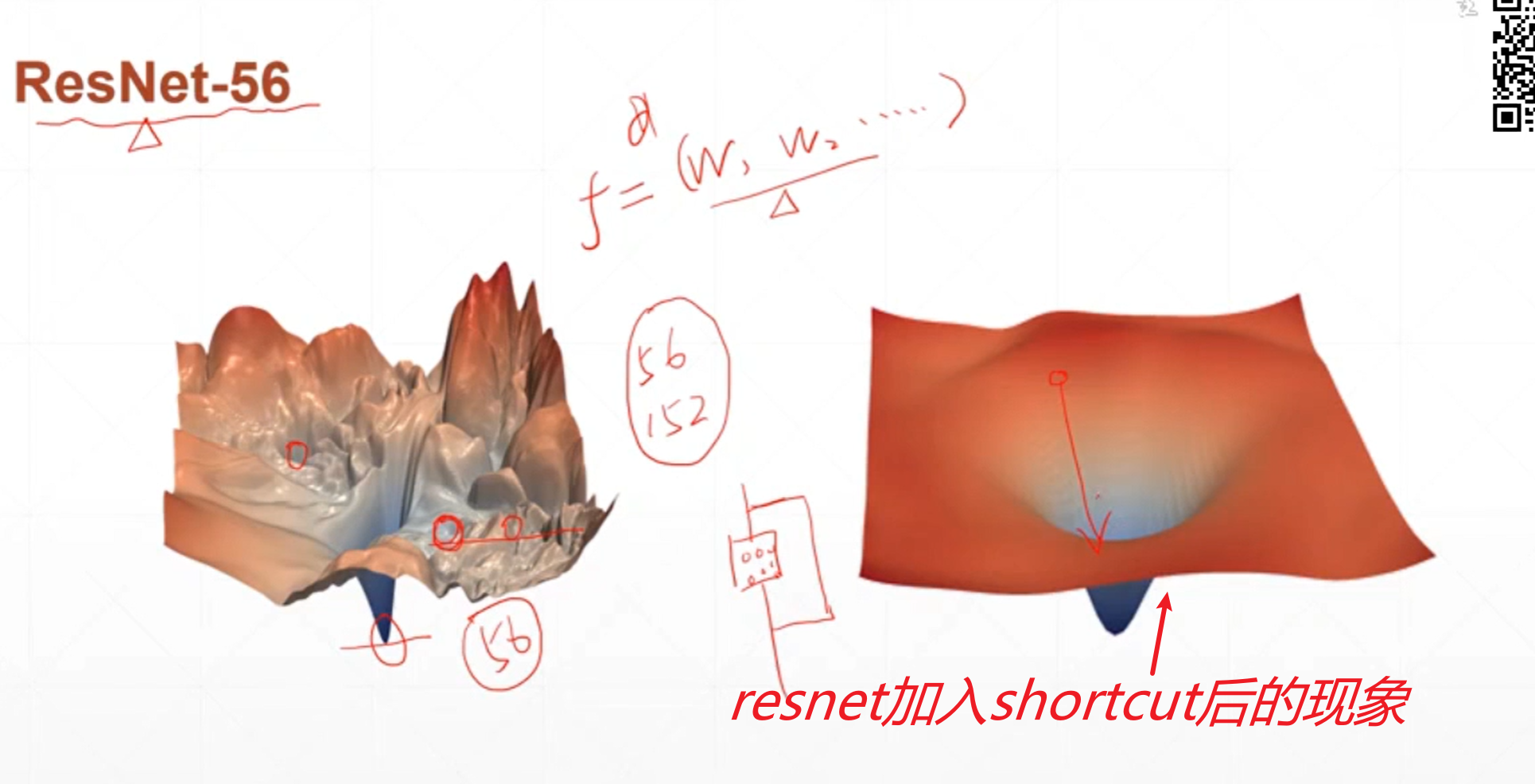
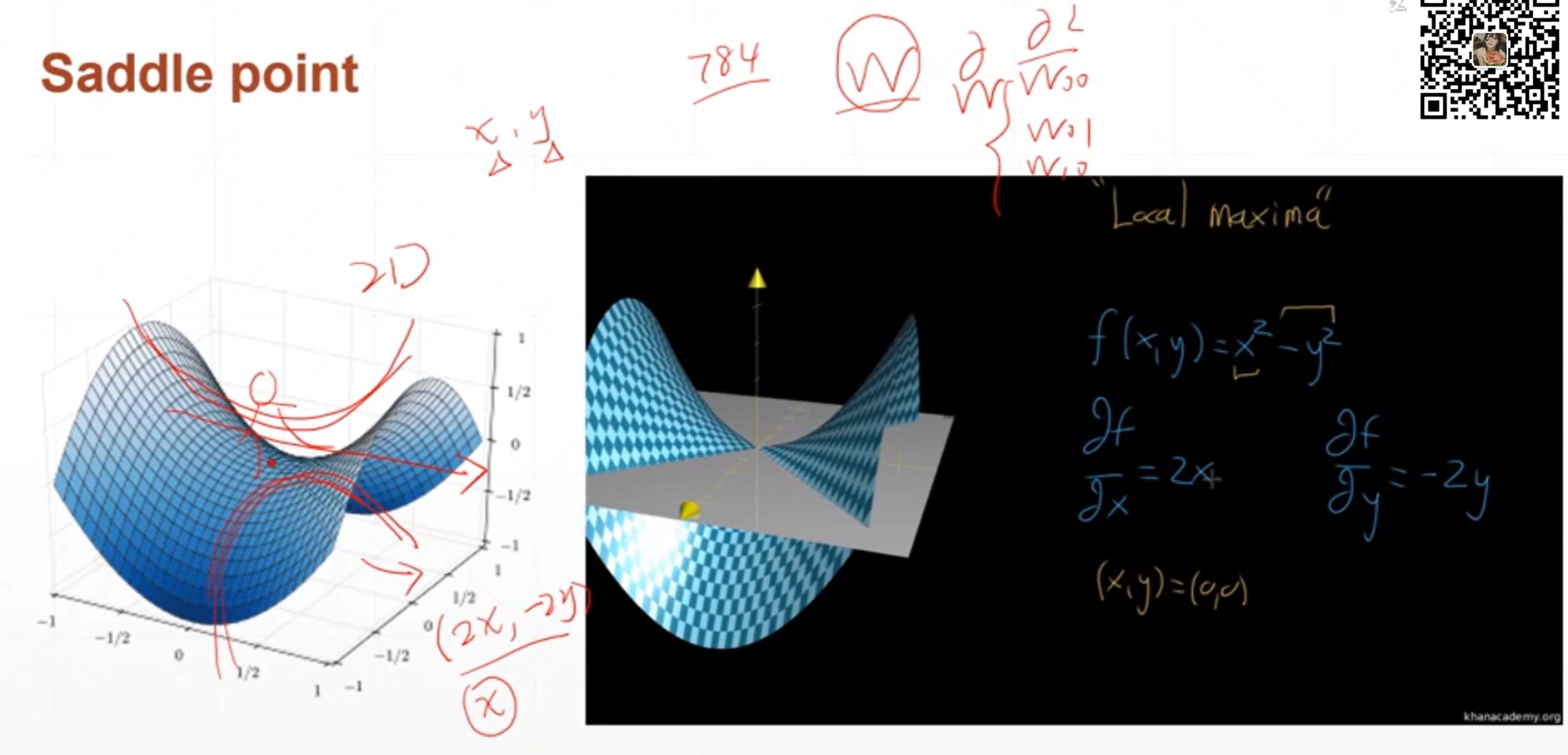
在马鞍点的时候损失函数在x上面取得的是局部最小值,在y方向上面取得的是局部最大值,就像手写数字识别一样有784个输入,那么就有成千上万个权重,假如是全连接神经网络很有可能在某一个自变量权重w的维度上面取得一个极小值但是在另外一个自变量权中w上面取得的是一个极大值,陷入马鞍点的极值点只会在这一点上周围来回震荡,或者只收到局部的极小值,这种现象比陷入局部极小值更可怕。
马鞍点现象和局部极小值的现象会影响到优化器搜索最小值的过程。
那么还有哪些参数会影响到优化器寻找最小值的过程呢?
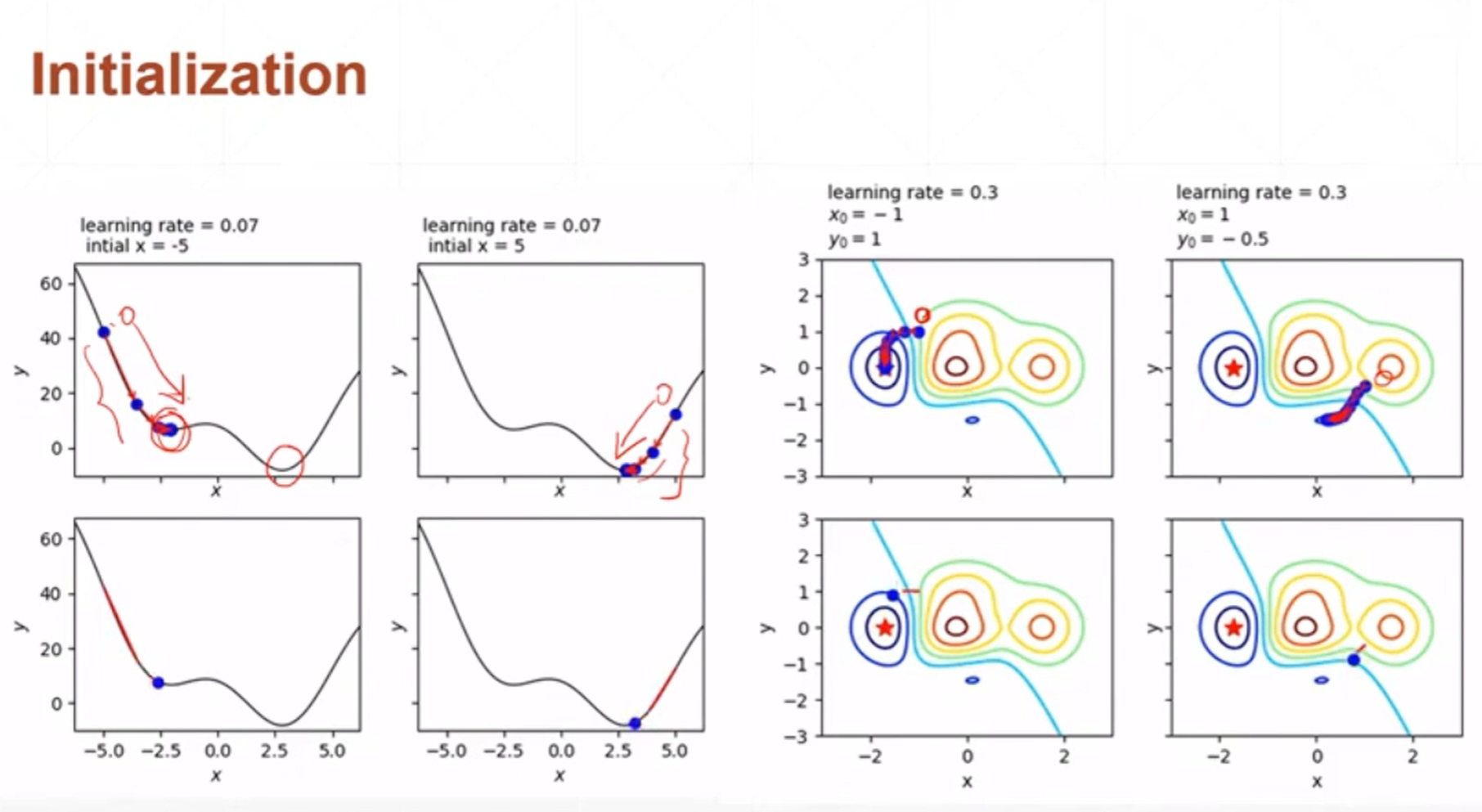
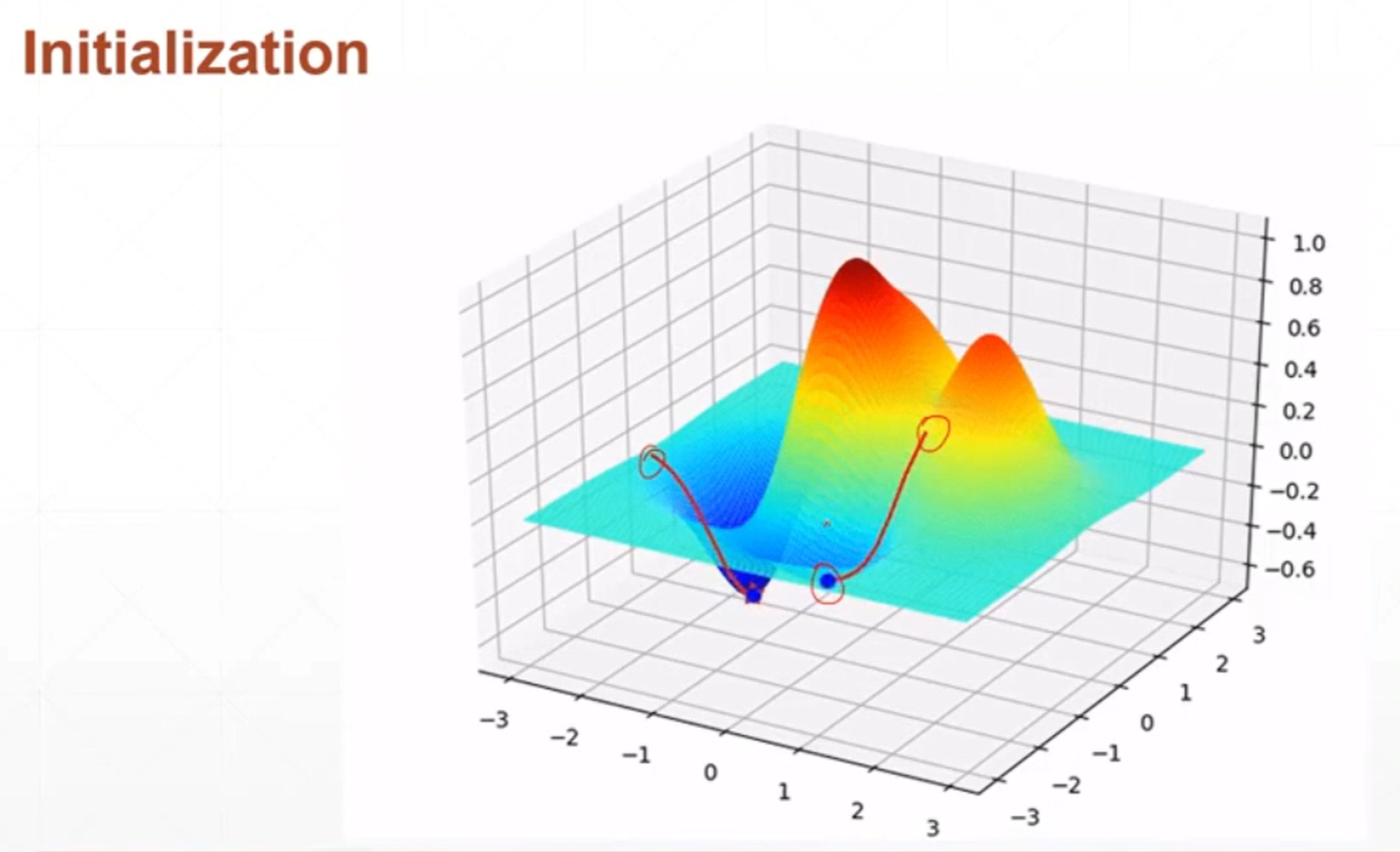
网络权重初始化的位置可能会影响到最终优化器收敛的位置。
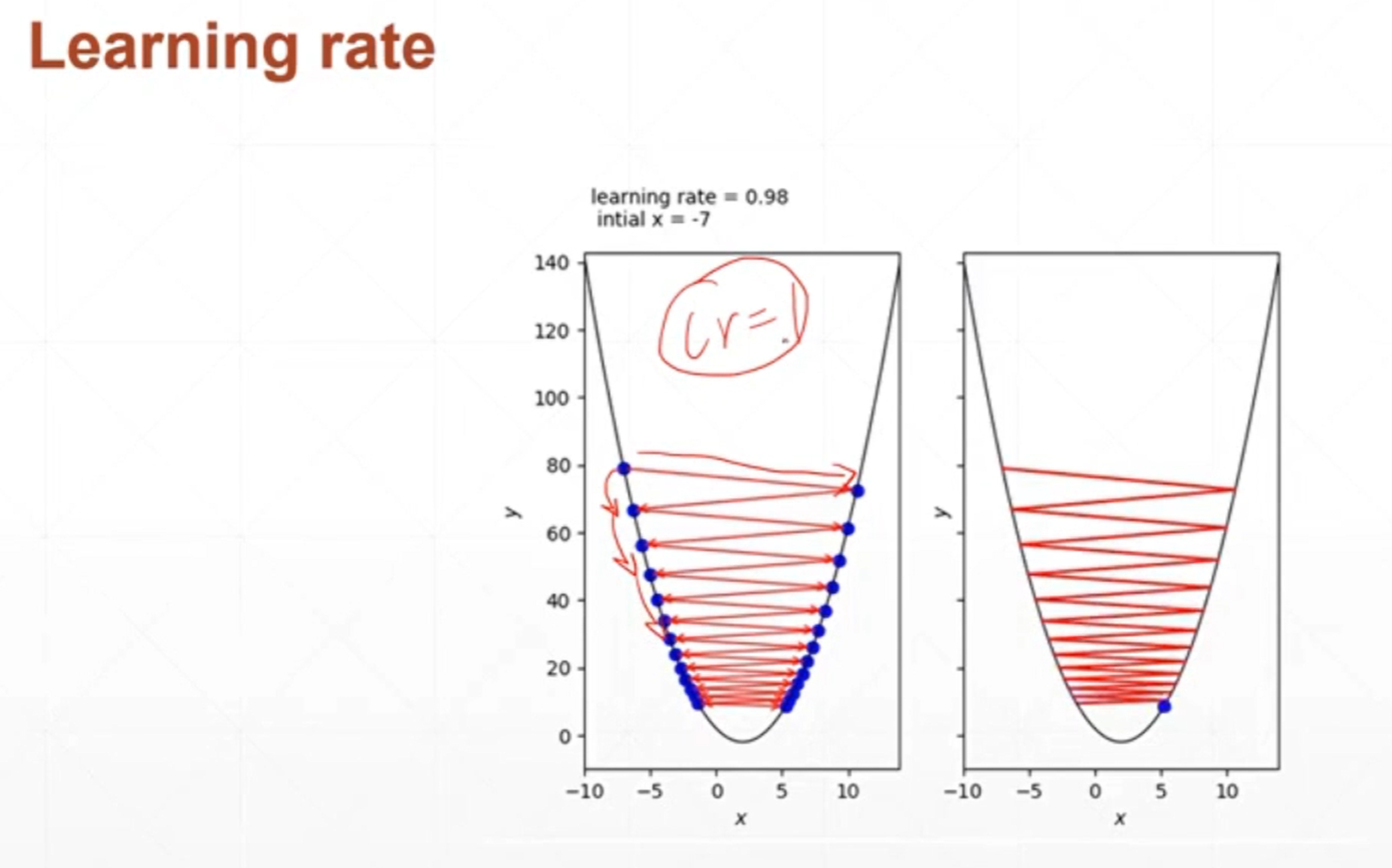
如果学习率设置的过大,那么很有可能会导致在收敛的过程当中来回震荡不能收敛。
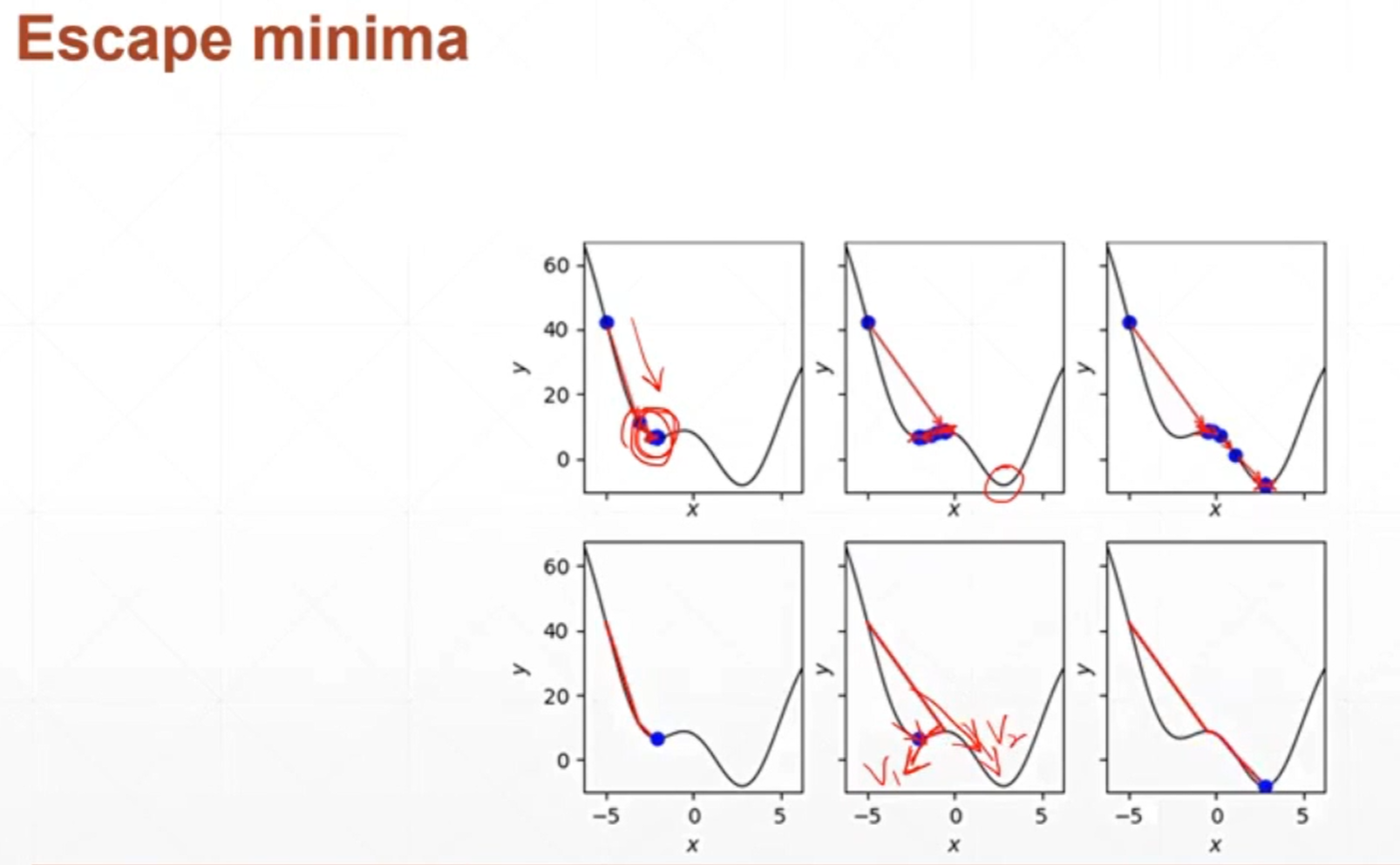
逃出最小值,逃出局部极小值,涉及到一个动量的问题。
课时36 常见函数的梯度_哔哩哔哩_bilibili
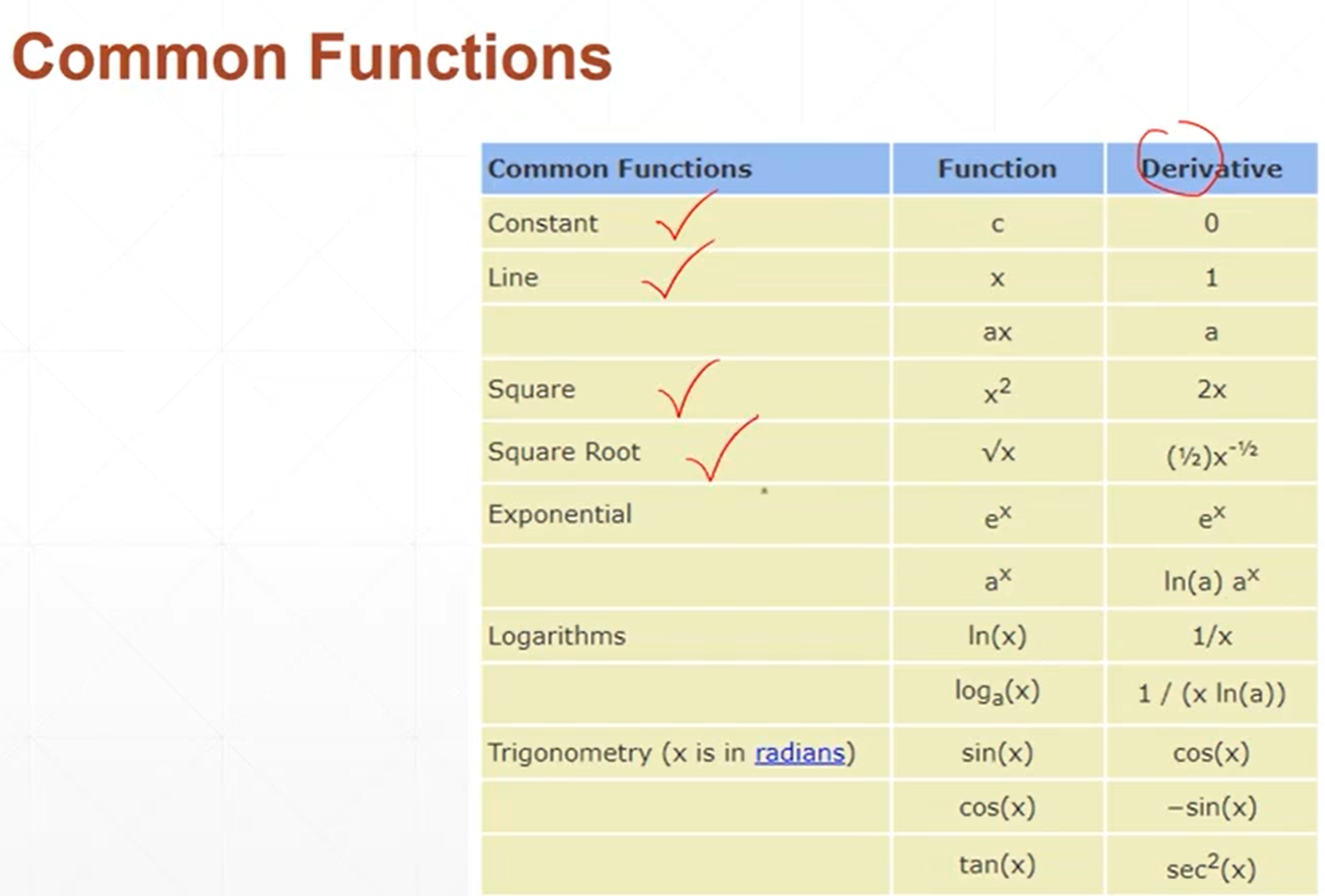
因为一维函数只有一个方向,所以它的导数和梯度基本上是一样的,只不过导数是一个标量,而梯度是一个向量。
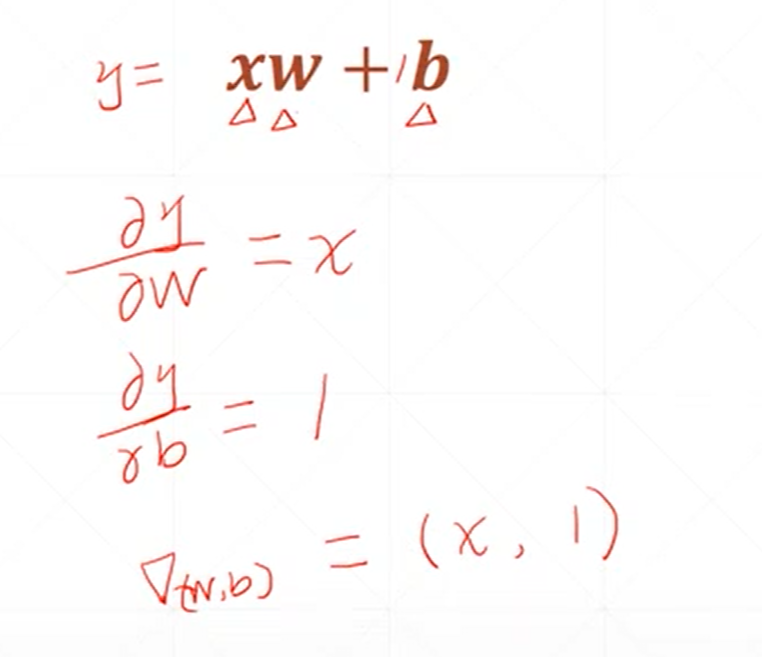
这是对一个感知机线性模型偏微分或者说梯度的一个求解。
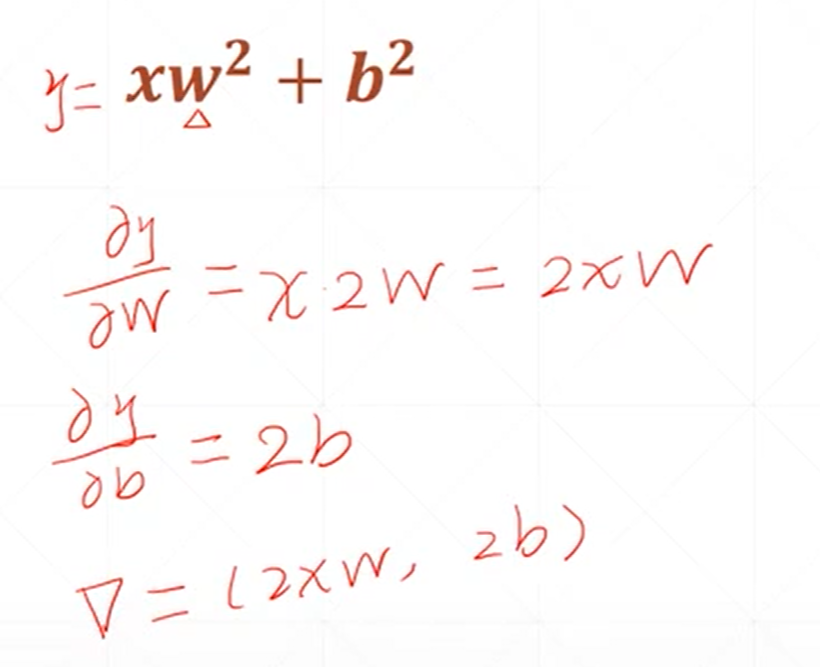
这是一个二次模型对未知参数求梯度的结果。
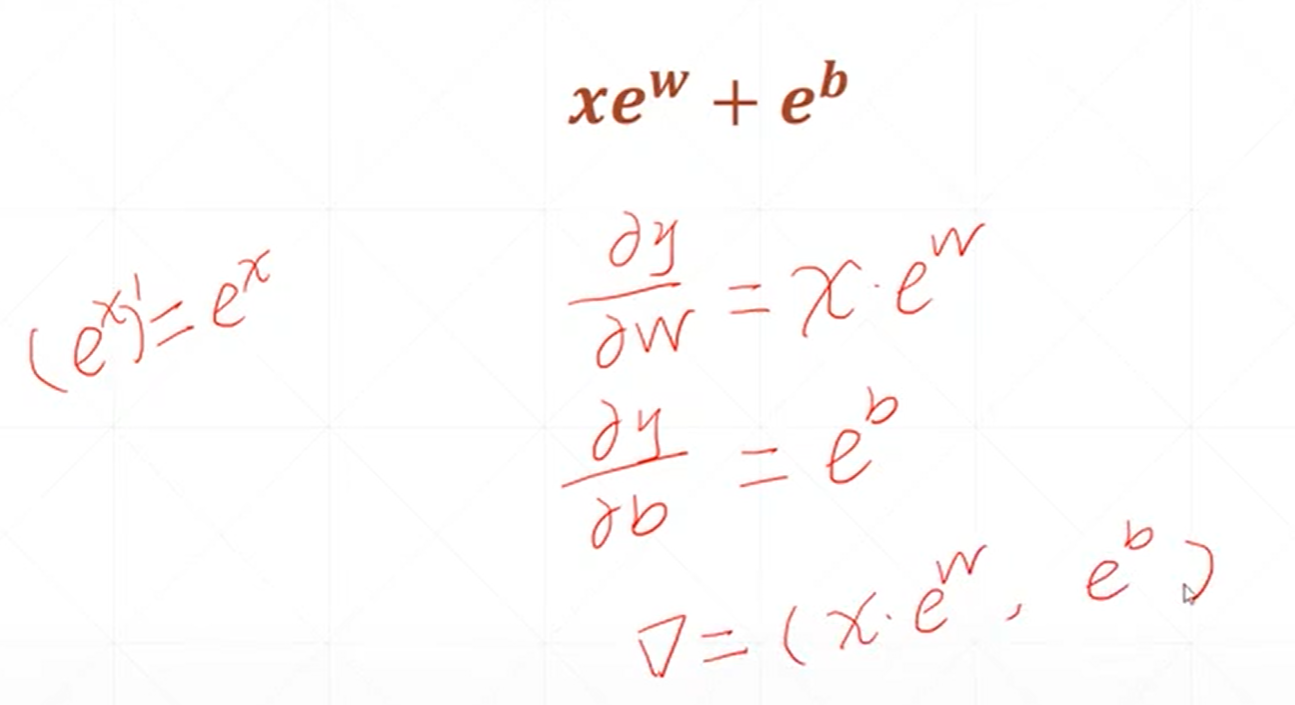
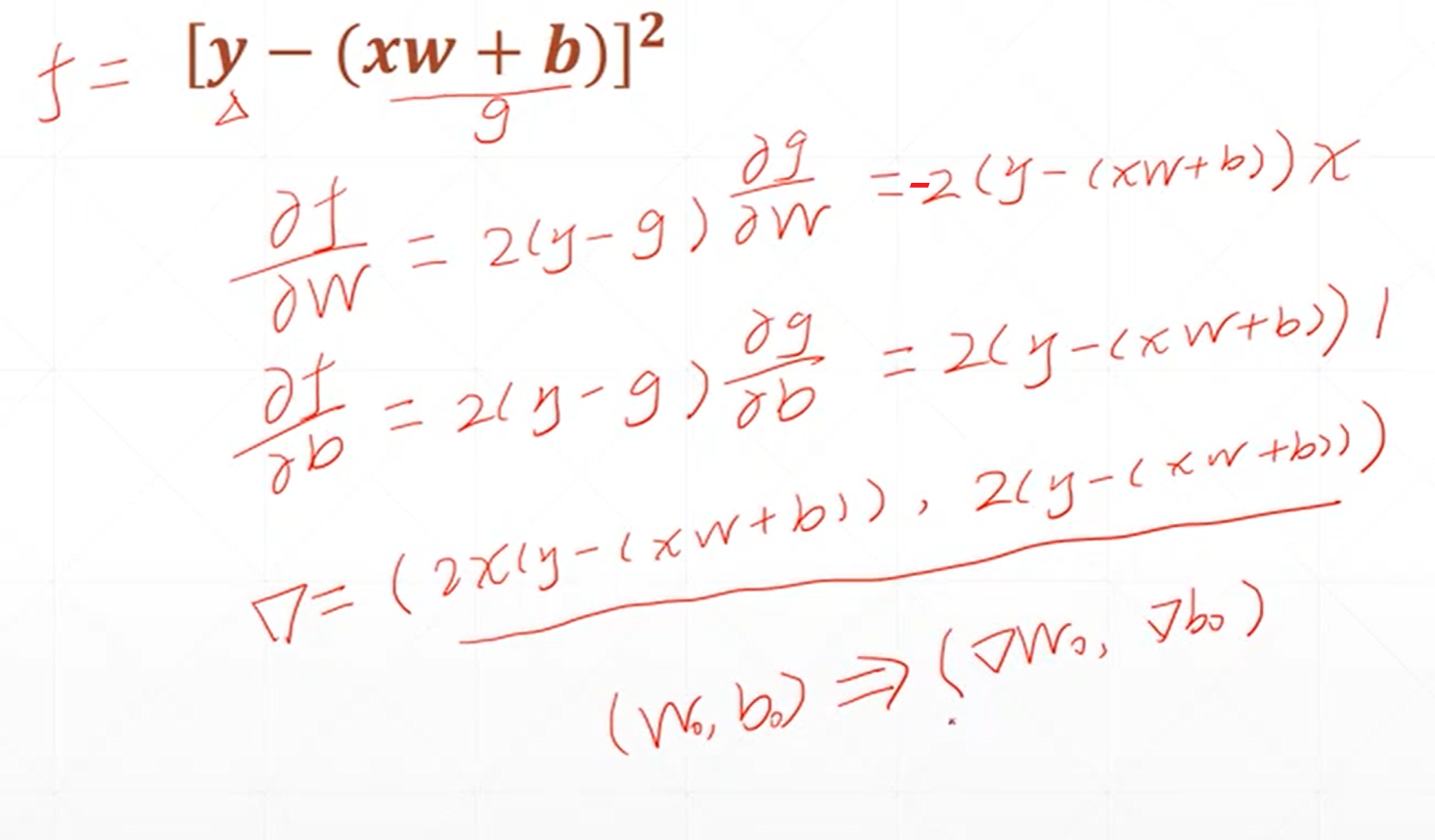
这个式子可以看做是一个感知机的输出和它的真实的标签之间的差的平方。
假如是单层的神经网络,那么根据W0、B0的初始化的值就可以对权重和偏置进行更新了。
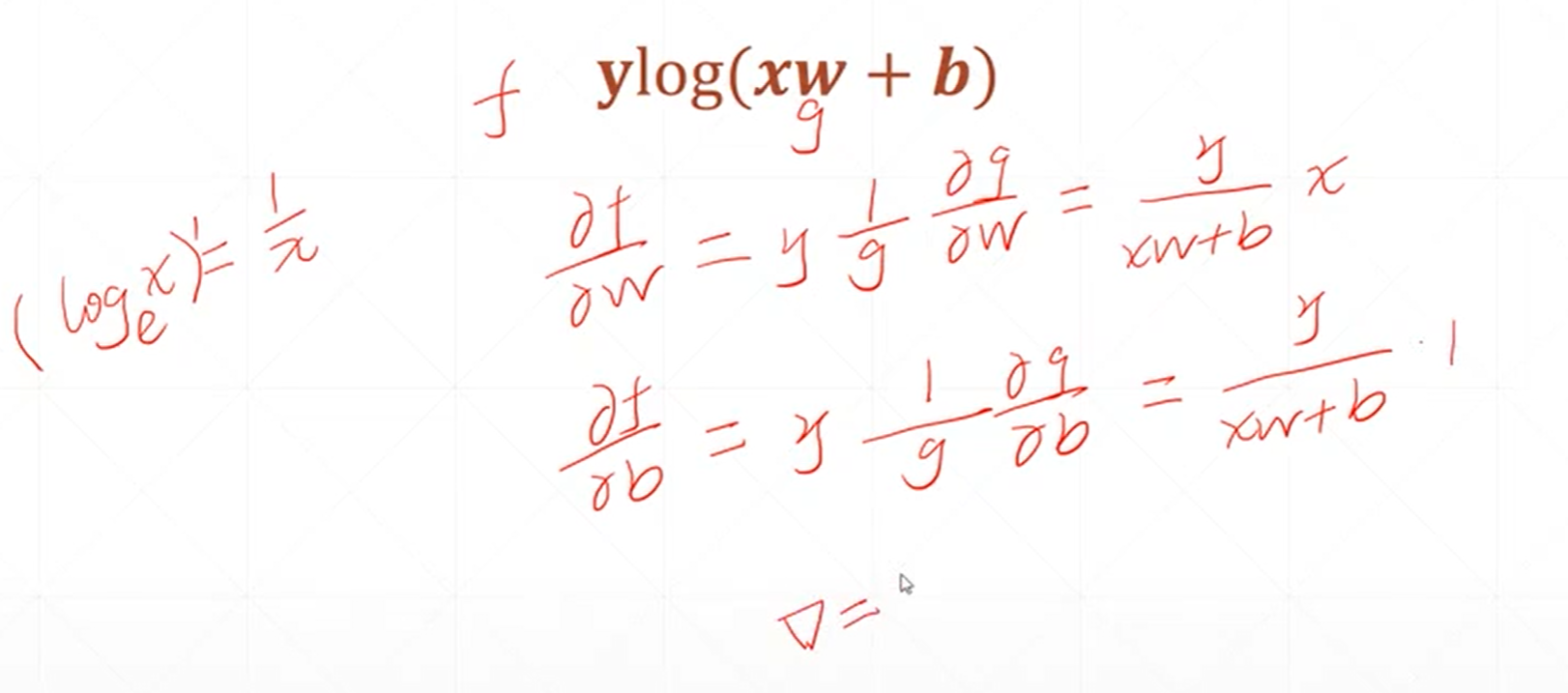
课时37 激活函数与Loss的梯度-1_哔哩哔哩_bilibili

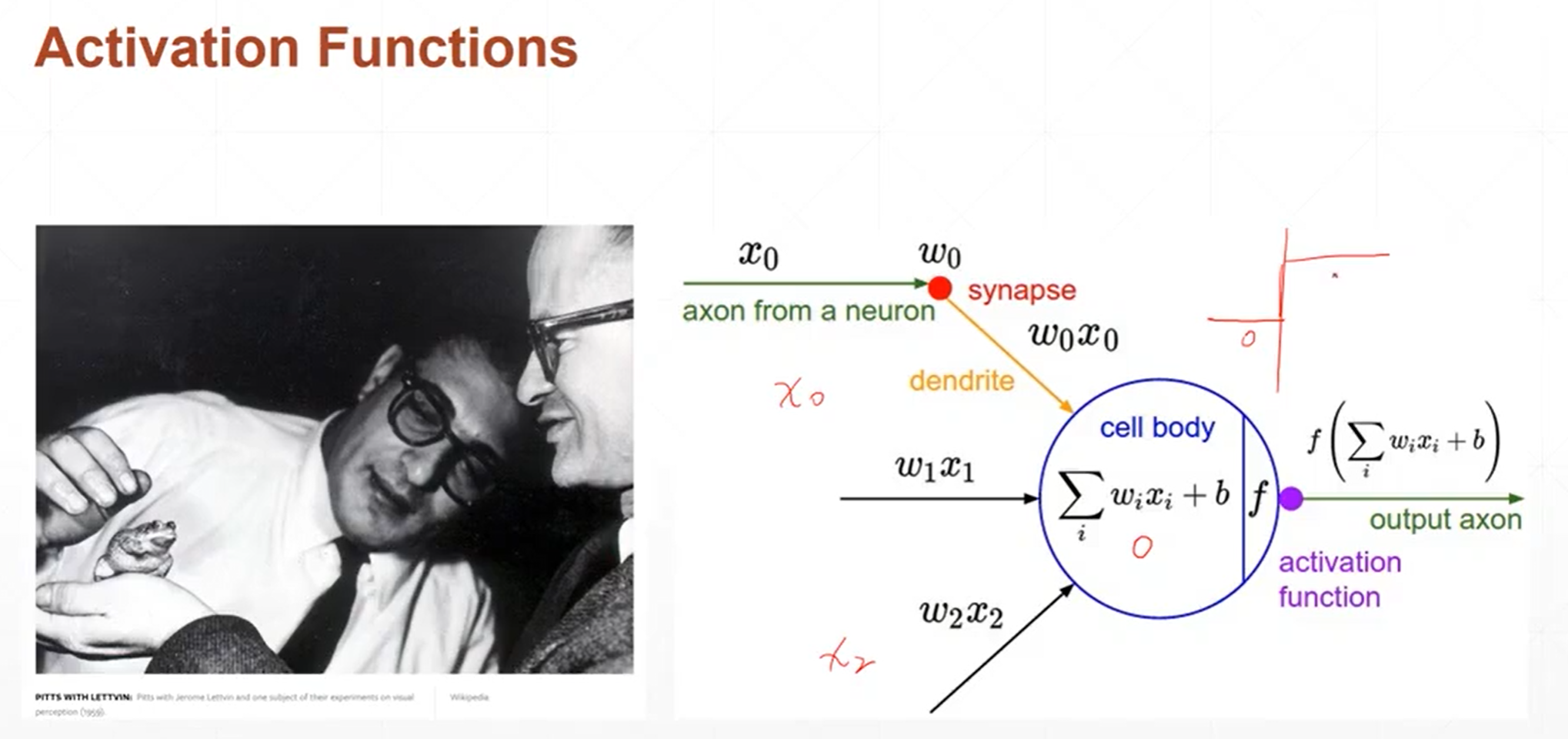
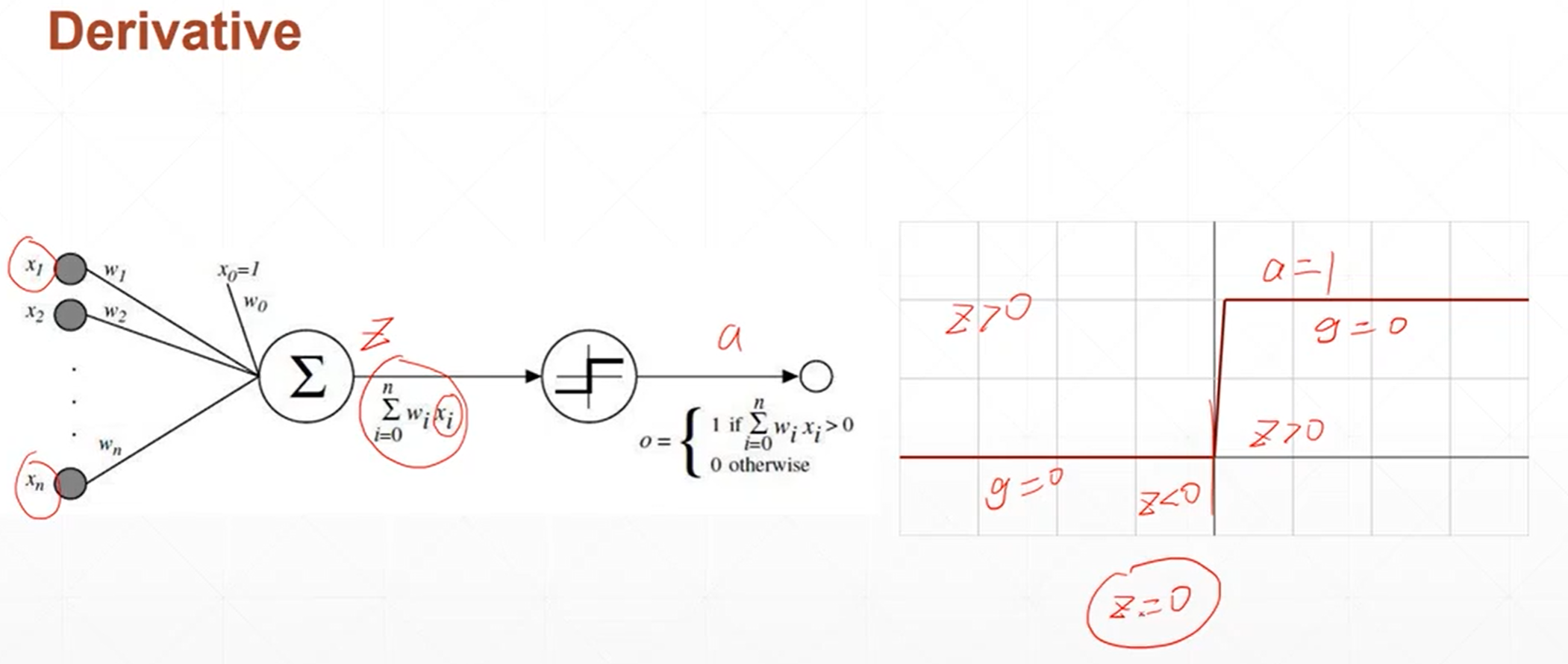
生物学家对青蛙的反应进行研究,发现青蛙的反应不是一个简单的线性输出,而是跟阈值有关系,当某一个刺激小于阈值的时候,他就没有响应,当某一个刺激大于这个阈值的时候,会做出固定的反应。输出是一个阶梯型的函数。
计算机科学家根据生物学家对于生青蛙的神经元的生物反应机制构造了发明了计算机上的一个模型。这个模型与生物的神经元模型非常相似。
单层神经元的激活函数不可导。为了解决这个激活函数不可导的问题,科学家提出了sigmoid激活函数。
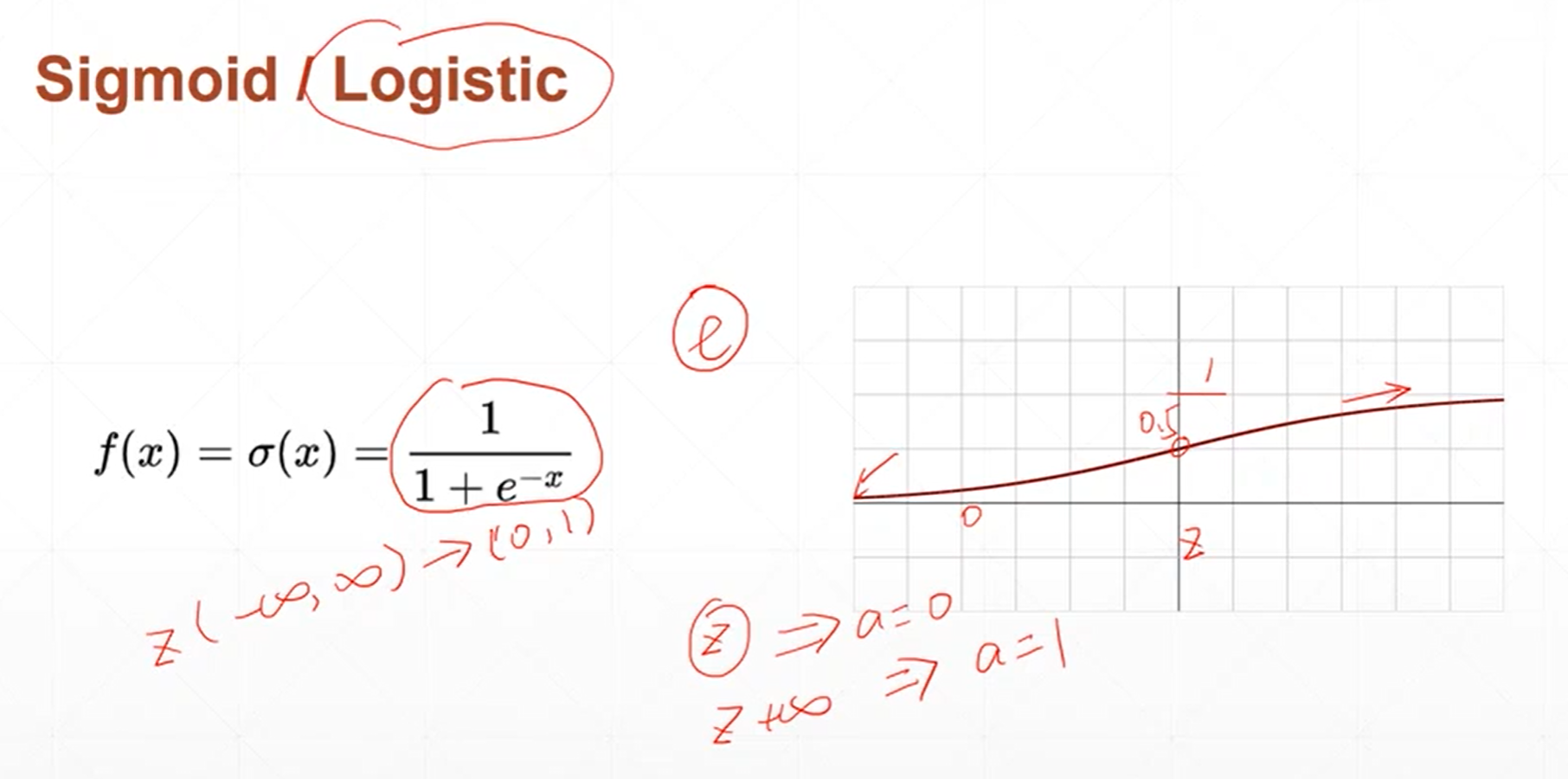
当自变量的值小于0的时候,函数的值接近于0,当自变量的值大于0的时候,函数的值接近于1。这个函数是非常光滑的,非常适合模拟生物学上神经元的机制。当神经元的输出比较小的时候,那我的函数值也接近于0,那就意味着不用激活,也就是说接近于不响应的状态。当神经元的输出比较大的时候,神经元的响应也不会很大,而是一个固定的响应。
这个函数的导数情况是当x趋于负无穷小的时候,导数趋近于0,当x逐渐增大的时候,导数也缓慢的增大。当x=0的时候。导数值增大到最大,当X继续增大的时候,导数值缓慢的减小,当X趋于无穷大的时候,导数值趋近于0。
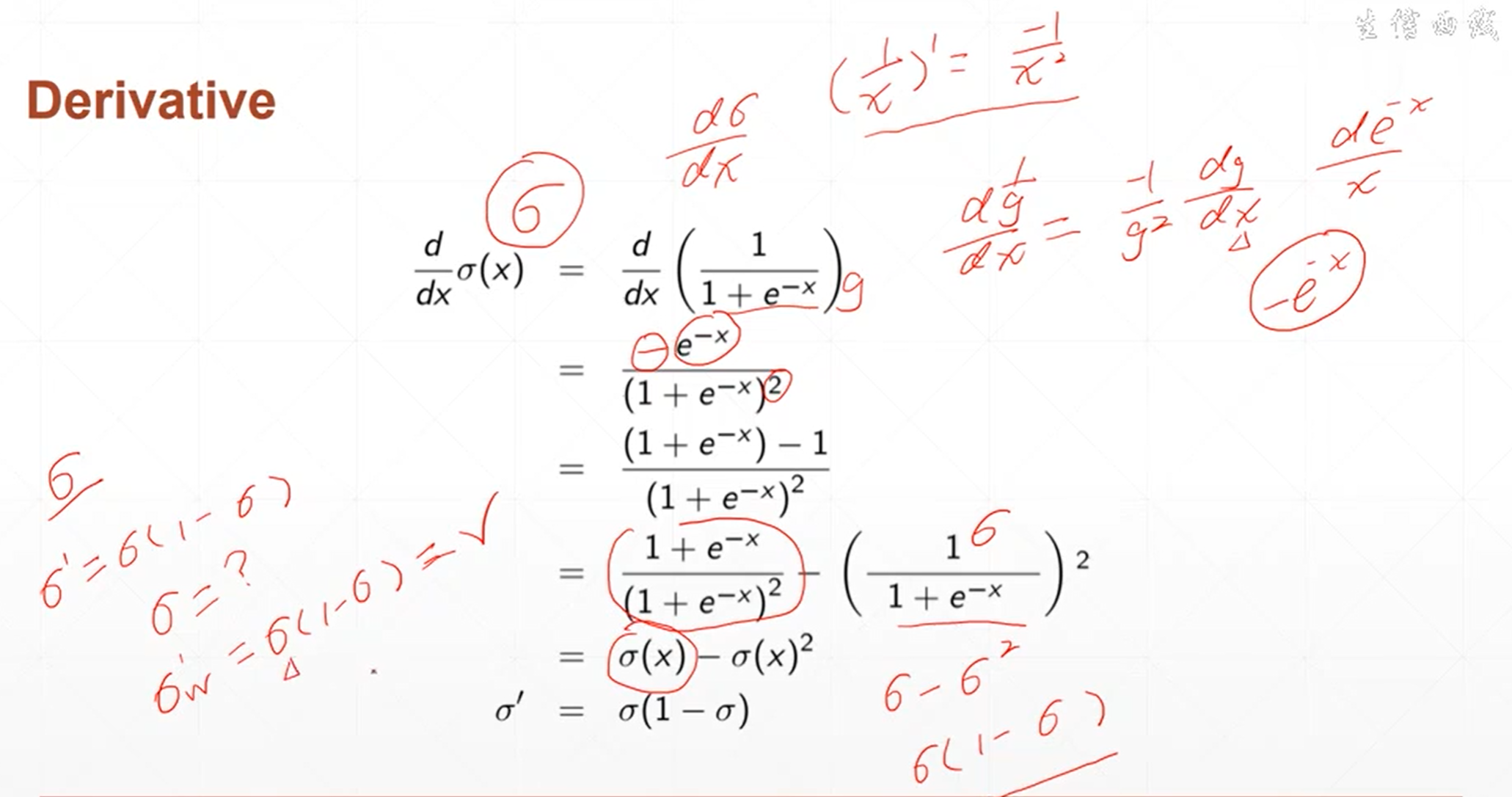
sigmoid函数的导数是非常有意思的,当前线传播的时候。 sigmoid函数值是一个已知的值,当反向传播的时候。需要用到sigmoid函数的导数,那它的导数值可以根据它的函数值计算出来。
sigmoid激活函数在深度学习中使用的场景特别多,最主要是因为它是连续的、光滑的。而且他能把所有的神经元的输出压缩到0~1之间。这个范围内的数值可以看成是概率。所以当涉及的分类问题的时候。这个激活函数就会经常出现。
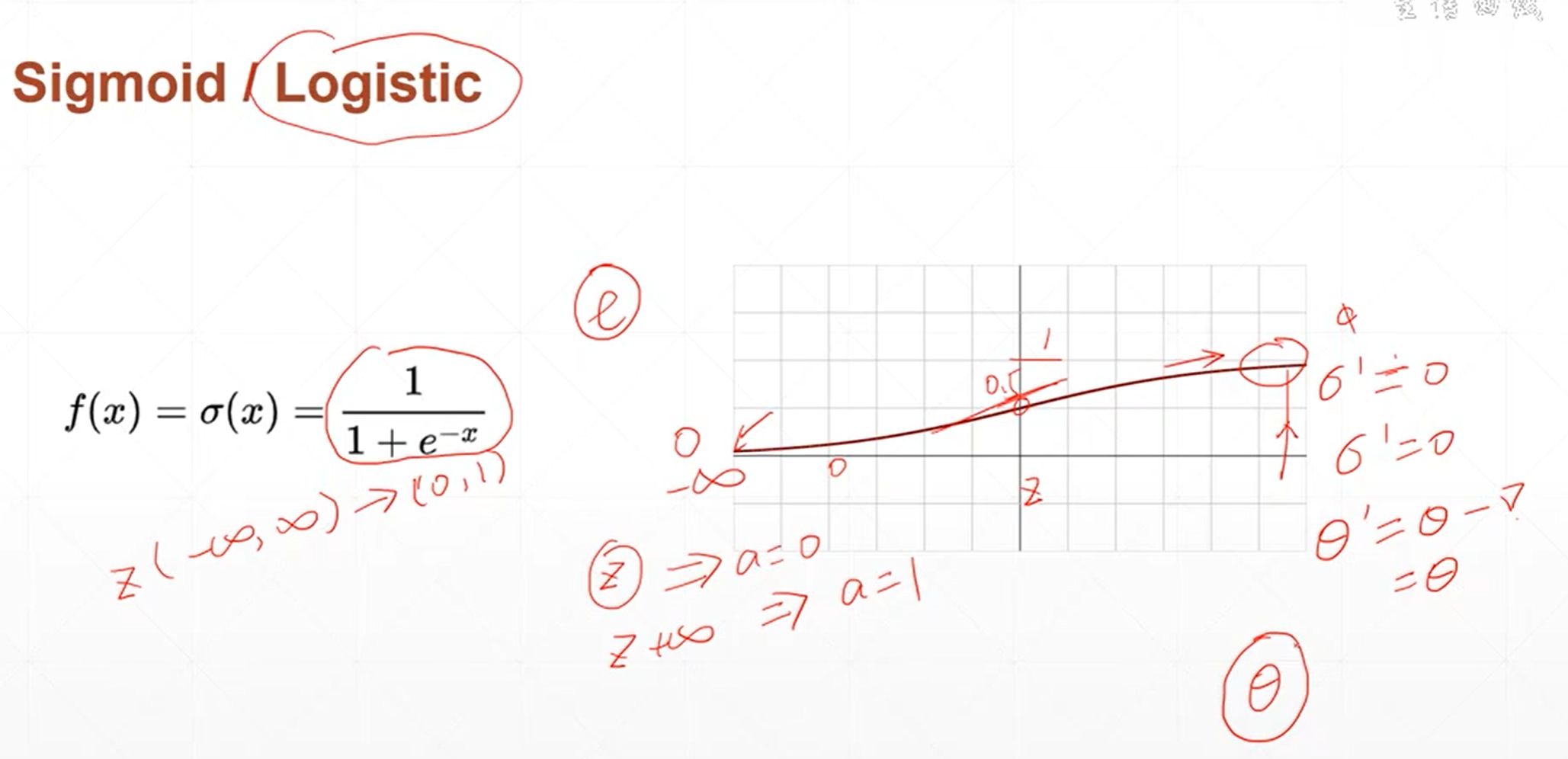
sigmoid函数也有一个致命的缺陷,就是说,当x很大的时候,它的导数值是趋近于0的。那参数在更新权重的时候就会。会出现很长时间很久得不到更新的情况,这个叫梯度消失。


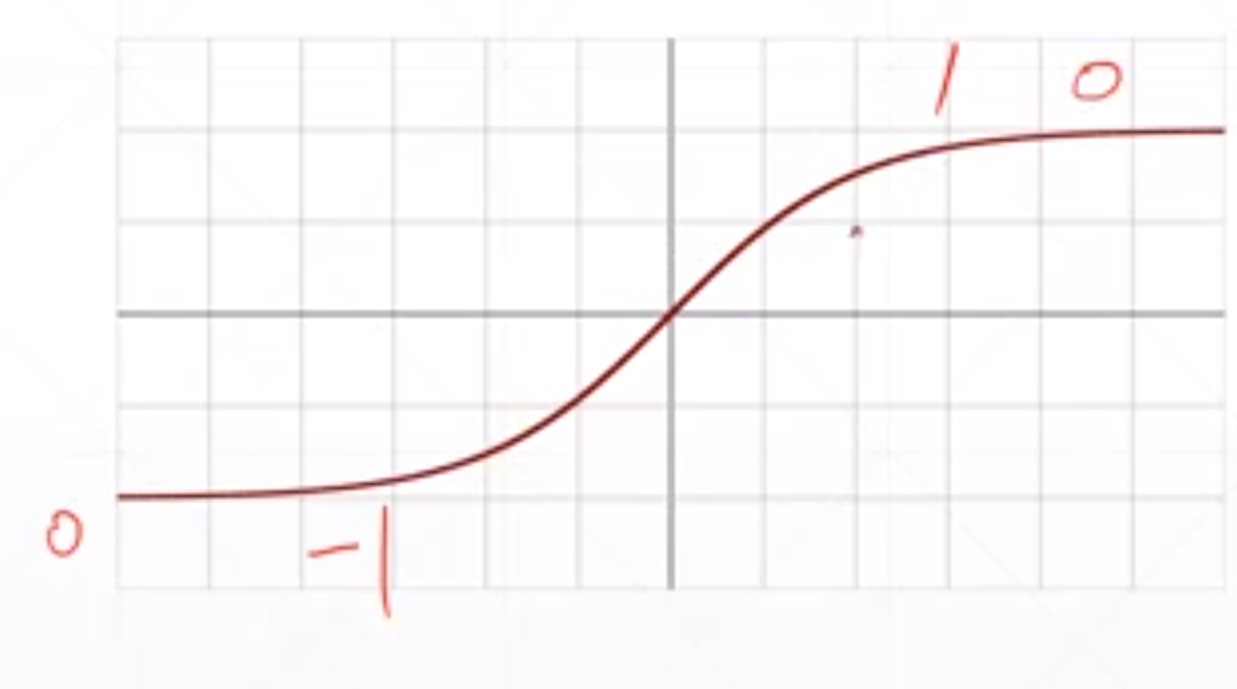
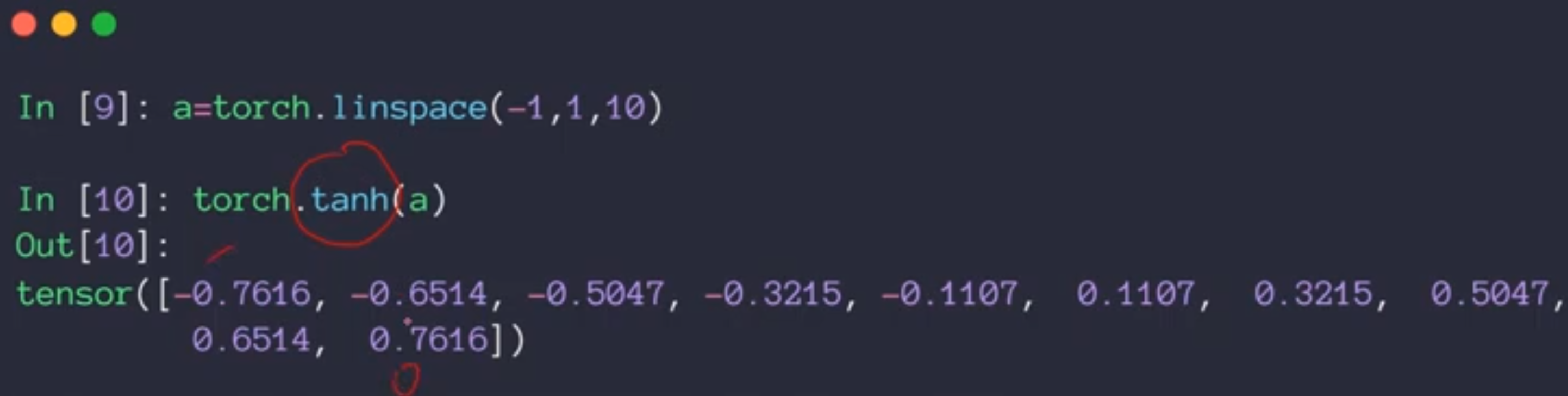
这个函数是通过sigmoid函数变换而来的,首先在X轴压缩1/2,然后在Y轴变成两倍。然后再减去一。在循环神经网络中用的多。
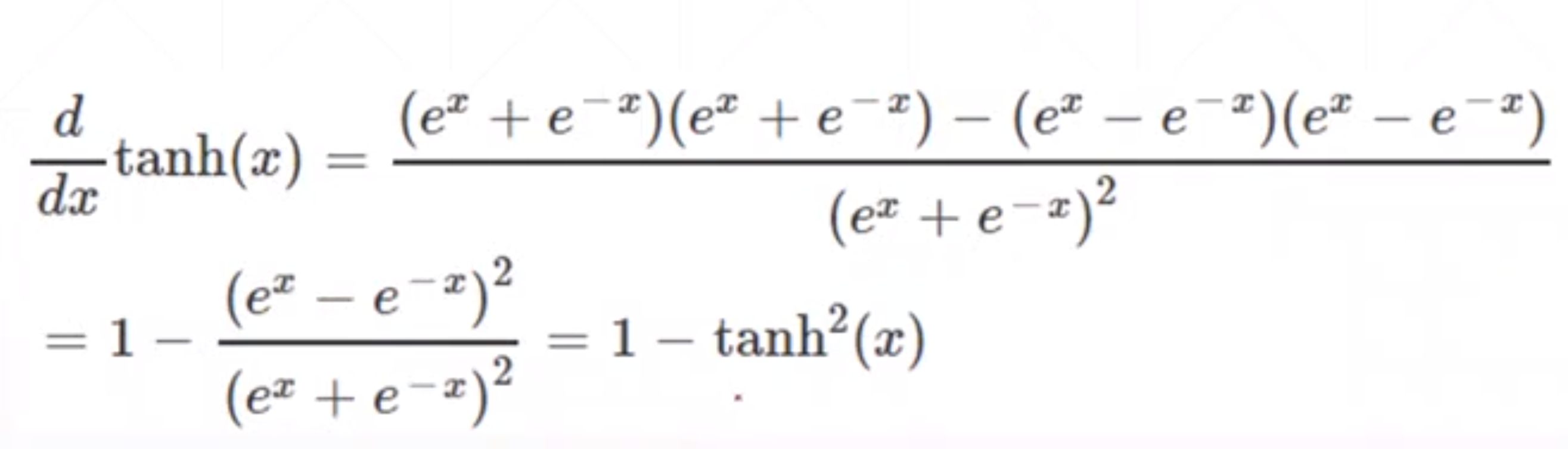
这个函数的导数值也是可以由其函数值直接可以得到。
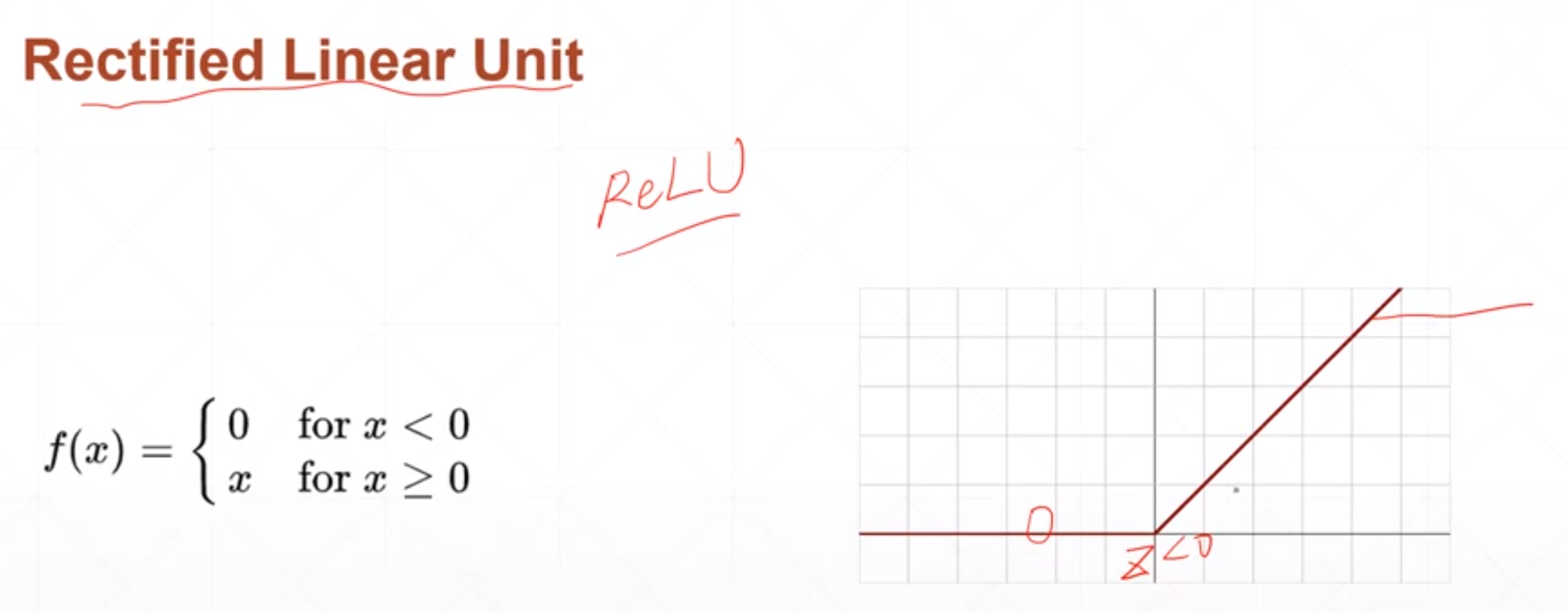
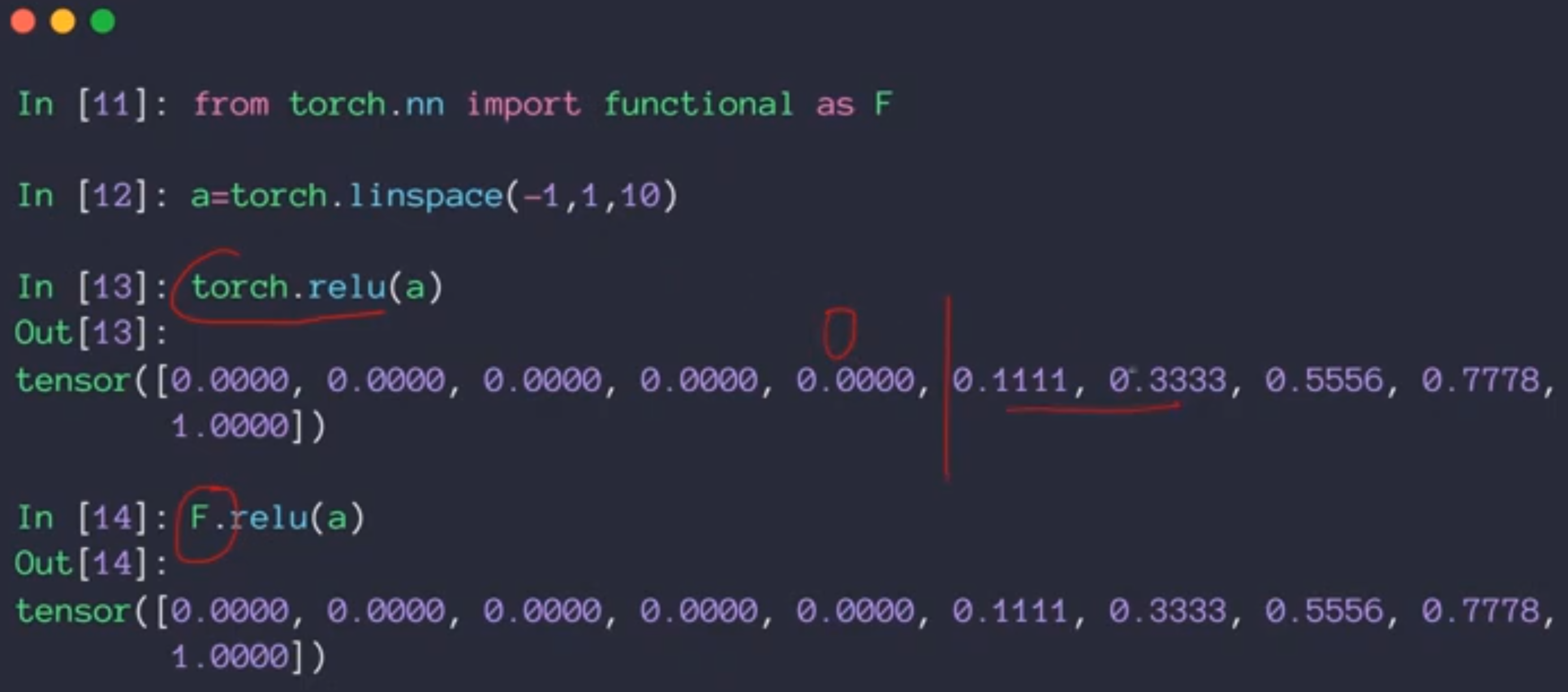
现在神经网络和深度学习使用最多的是relu激活函数,这个激活函数是现代深度学习的奠基石。
当神经网络的输出值Z小于0的时候,我就不响应,当Z>0的时候,我就线性的相应。
这个和感觉上的生物机制还不太符合感觉上的生物机制是当Z值很大的时候我要做一个限制,就是说当Z值很大的时候,我也是一个固定的输出。但是无数的深度学习的例子证明relu函数非常适合做深度学习的激活函数。
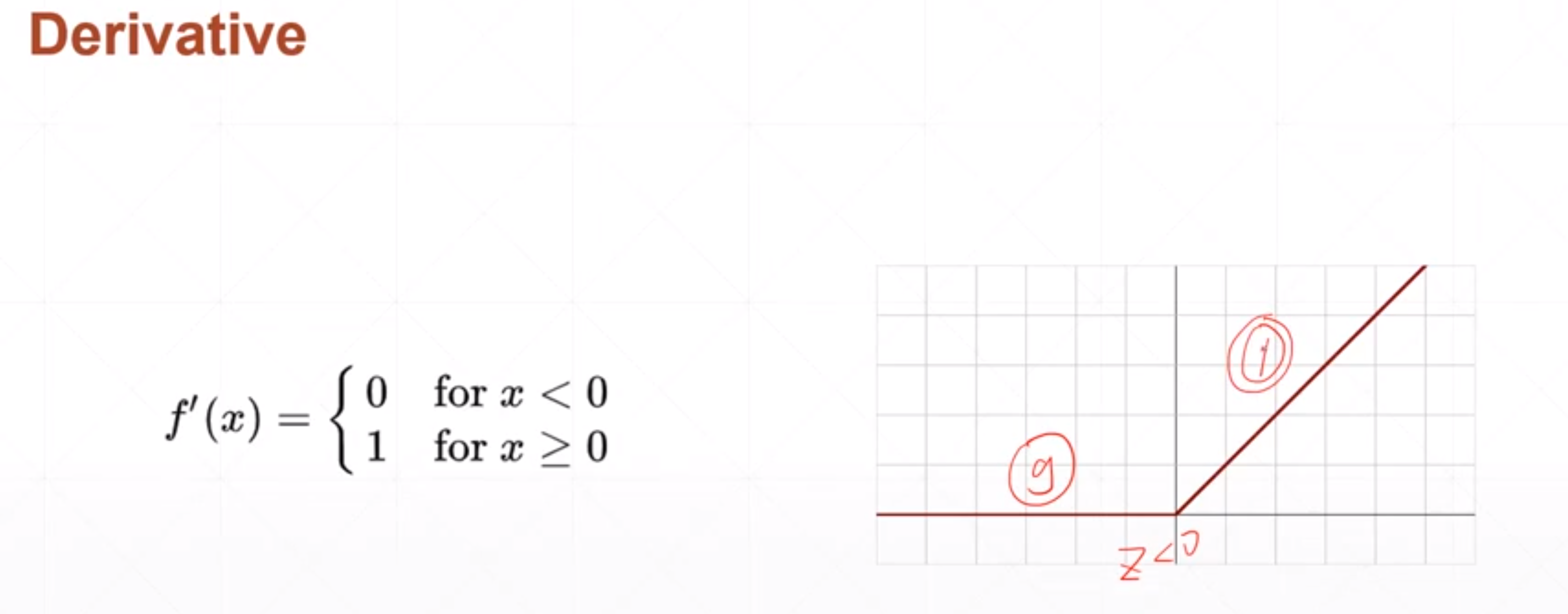
当Z值大于0的时候,它的导数值是保持1,神经网络在做反向传播的时候就不会发生梯度爆炸或者梯度消失的情况。
课时38 激活函数与Loss的梯度-2_哔哩哔哩_bilibili






