条件平差
例子:
三角形内角观测:
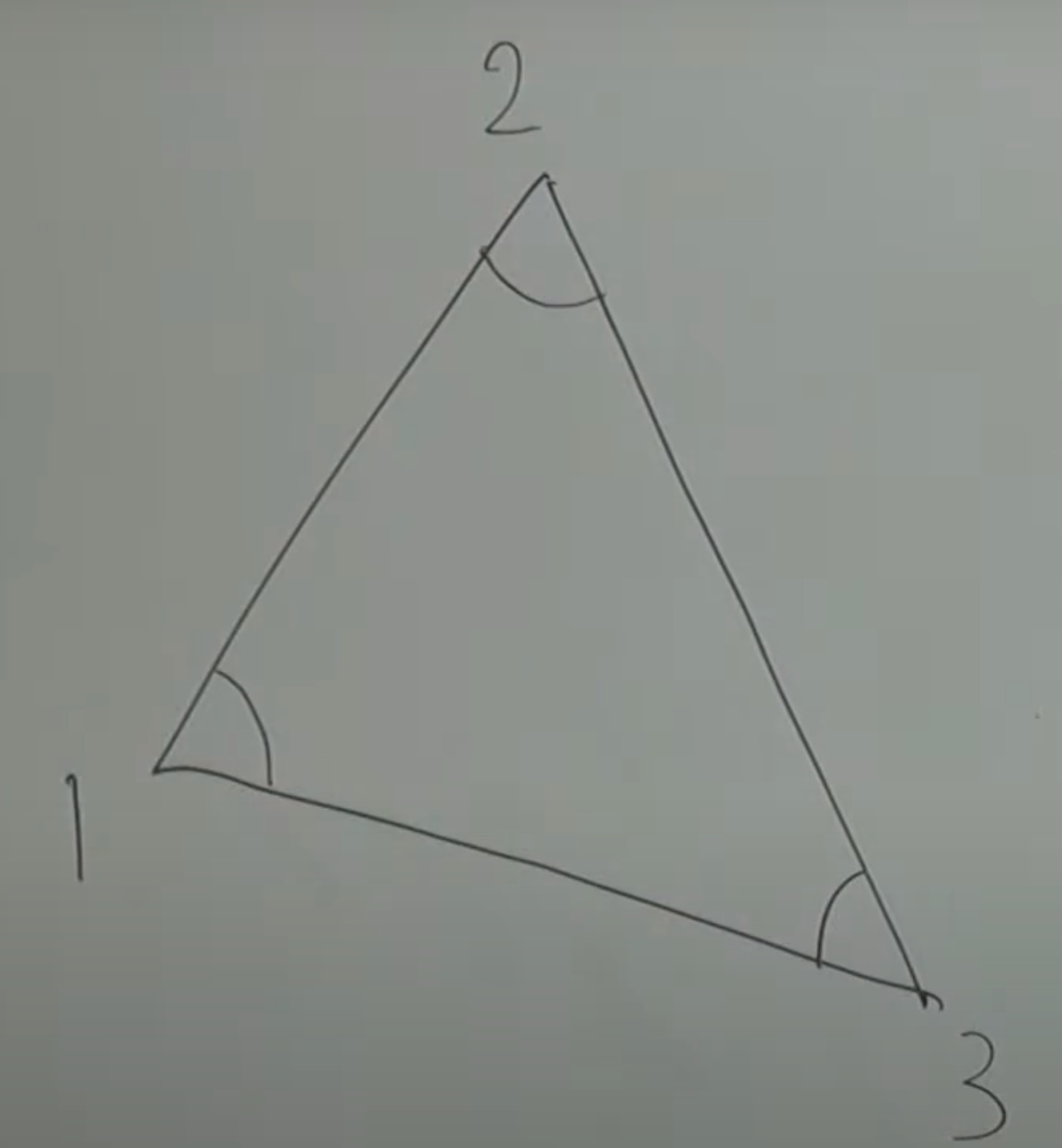

注解:
1.上面这个方程是观测方程,这个方程里面有3个未知数,一个方程解3个未知数是不可能解出来的,下面把这个方程表示成矩阵的形式:

注解:
1.小写c代表的是条件的个数,字母n代表的是观测量的个数,在这个矩阵方程里面,有c=1个观测条件,有n个观测量,小写的v代表的是误差向量,也可以说是不符值向量,小写的 L是一个常数值,观测向量或者说观测的个数N可以有很多很多可以有成百上千个,而条件的数量也可以有很多可以有上百个。
2.矩阵就是大写,向量就是小写。
3.注意,Bv-l=0向量。
平差模型:
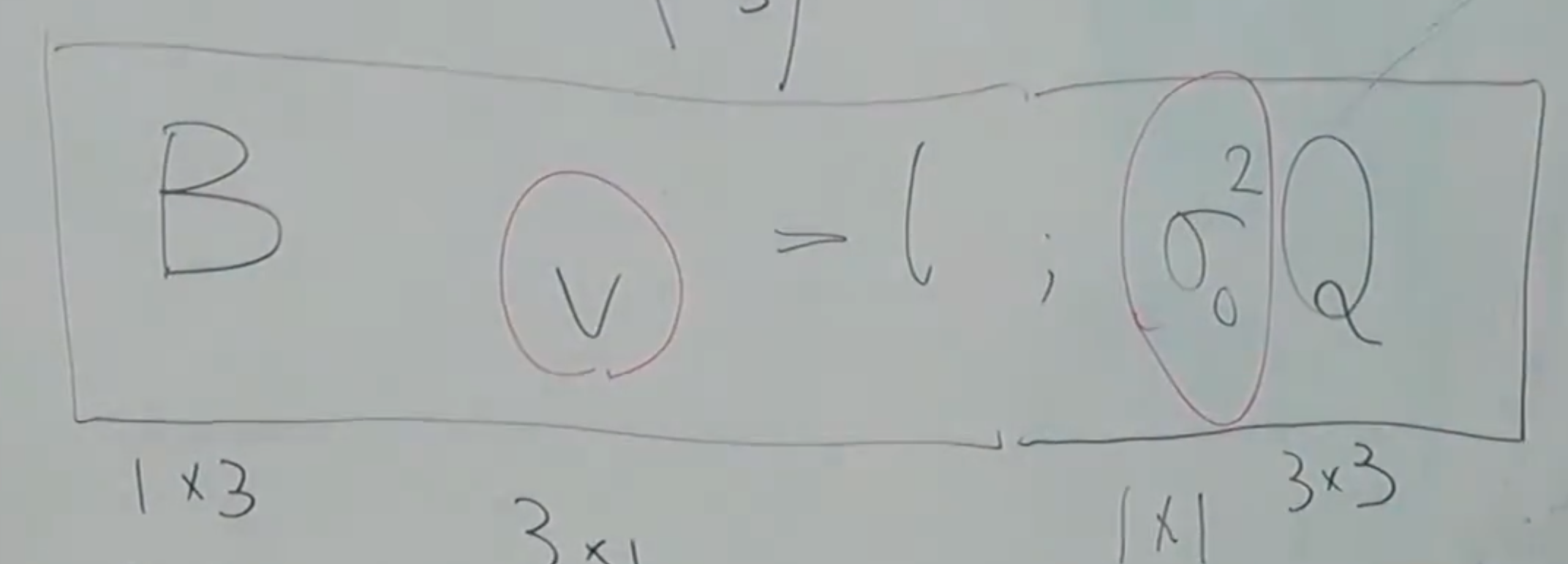 (1)
(1)


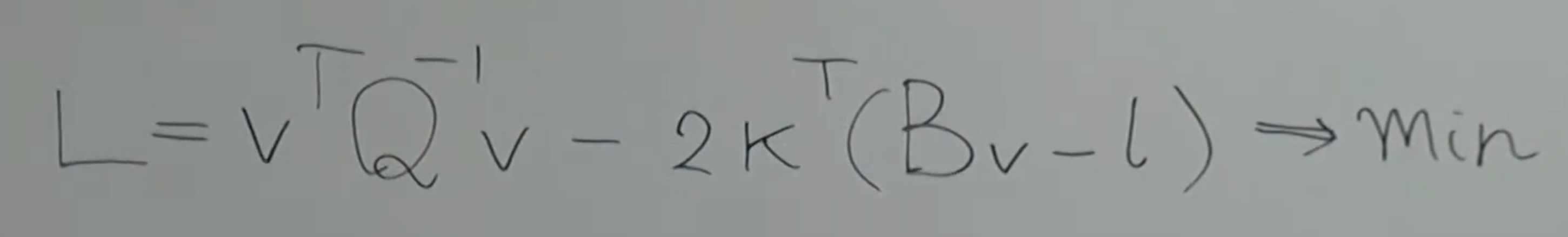
注解:
1.σ02我们不知道是多少,令其等于1,后面的推导会发现,结果不受它不等于1的影响,可大可小,都没关系,答案不变。
2.因为权阵中的元素是没有单位的,所以,必须给协因数阵一个尺度,让其变为无单位量纲的权阵。
3.K是拉格朗日乘子。
4.2也可以是任何的数字,因为后面括号里面的值是0.
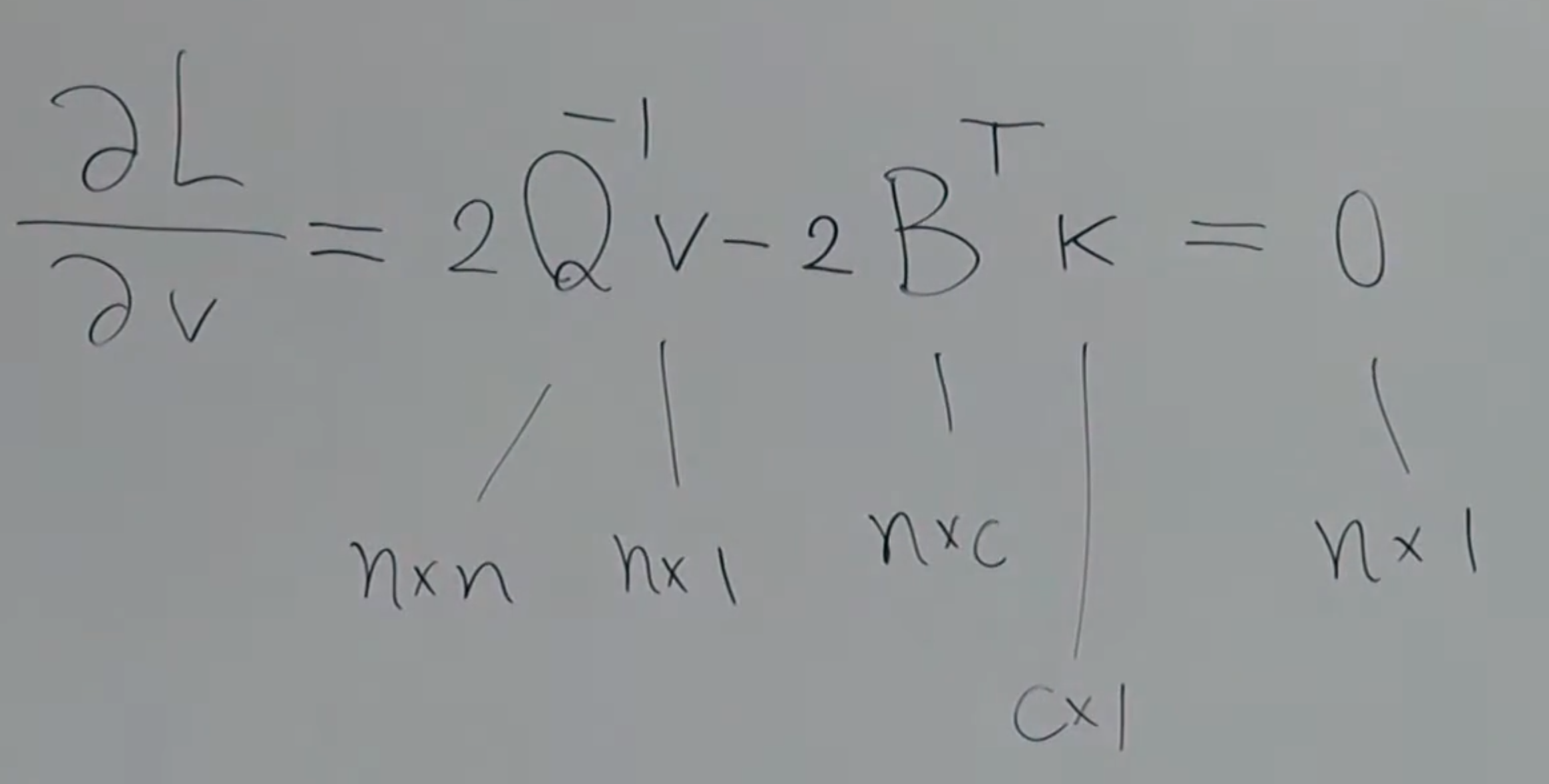
注解:
1.一个纯量对一个向量求偏导,那结果是一个向量。
2.求极值就意味着要微分。
3.未知数的个数是c个小k和n个小v,共有n(观测值改正值)+c个未知数(拉格朗日乘子)。在这个问题里面,n=3,c=1.
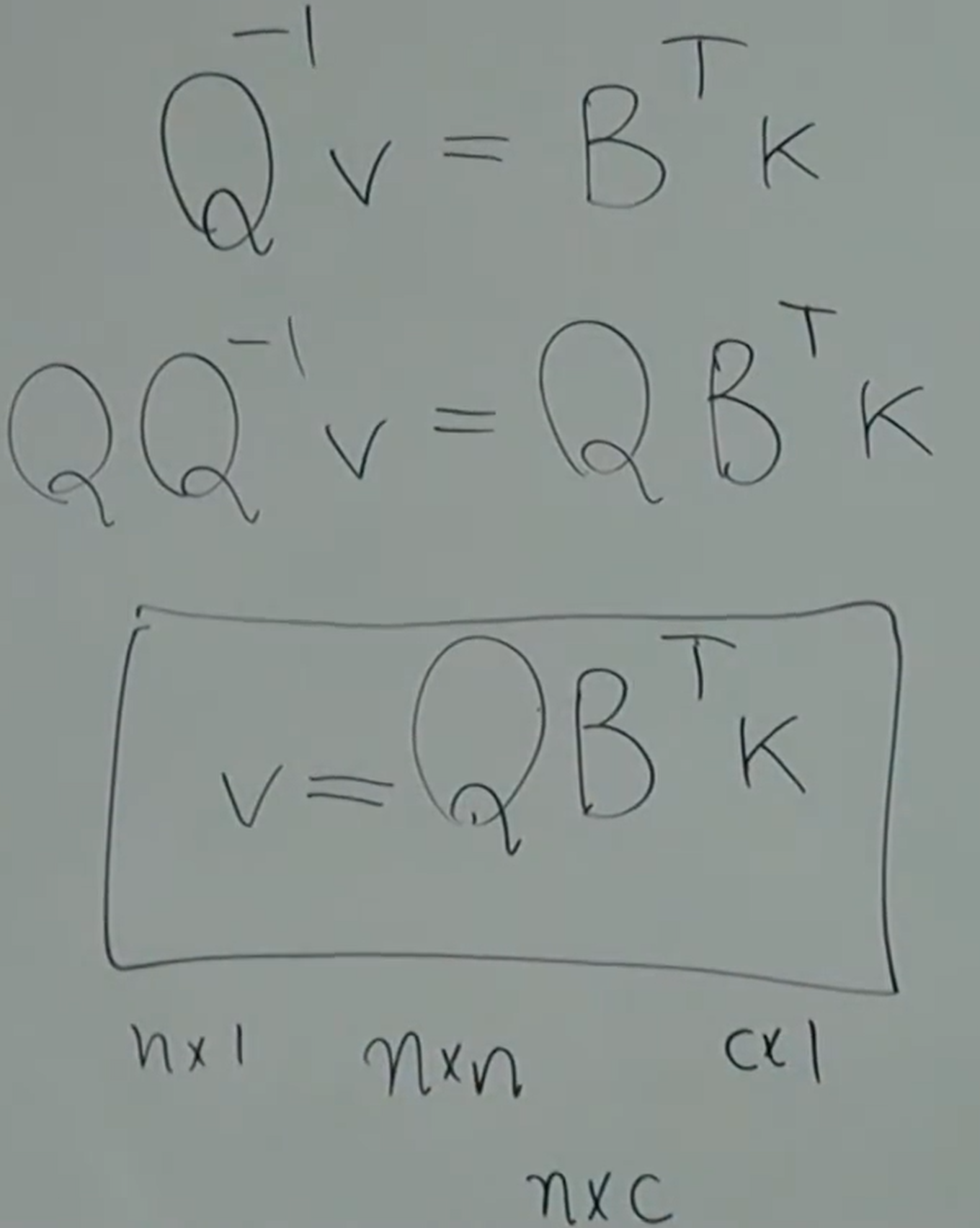 (2)
(2)
(2)带入(1):

注解:
1.B秩足,Q秩足,乘出来的东西也是秩足的方阵,可以对其取逆,没有秩亏的问题。
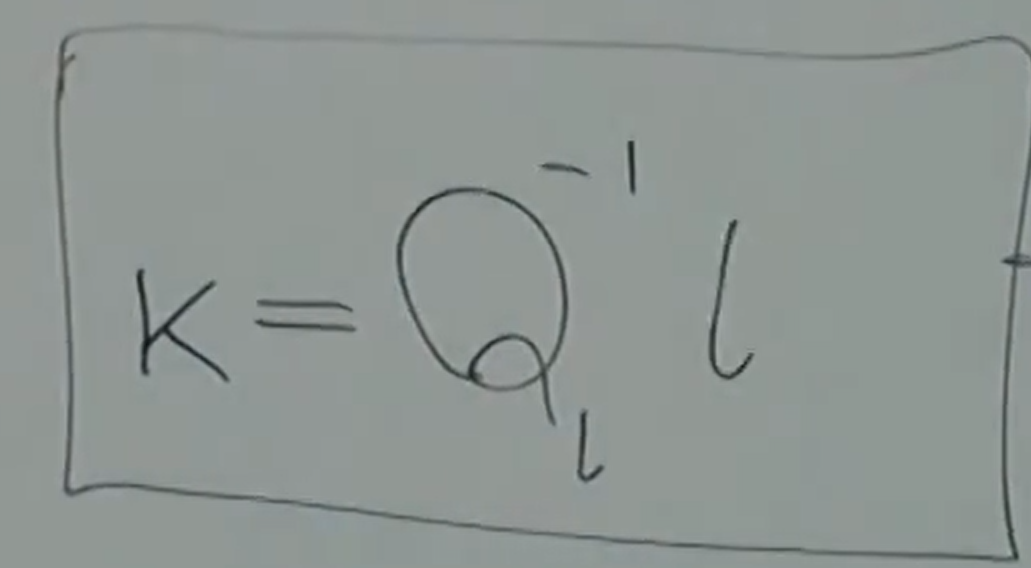 (3)
(3)
(3)带入(2):
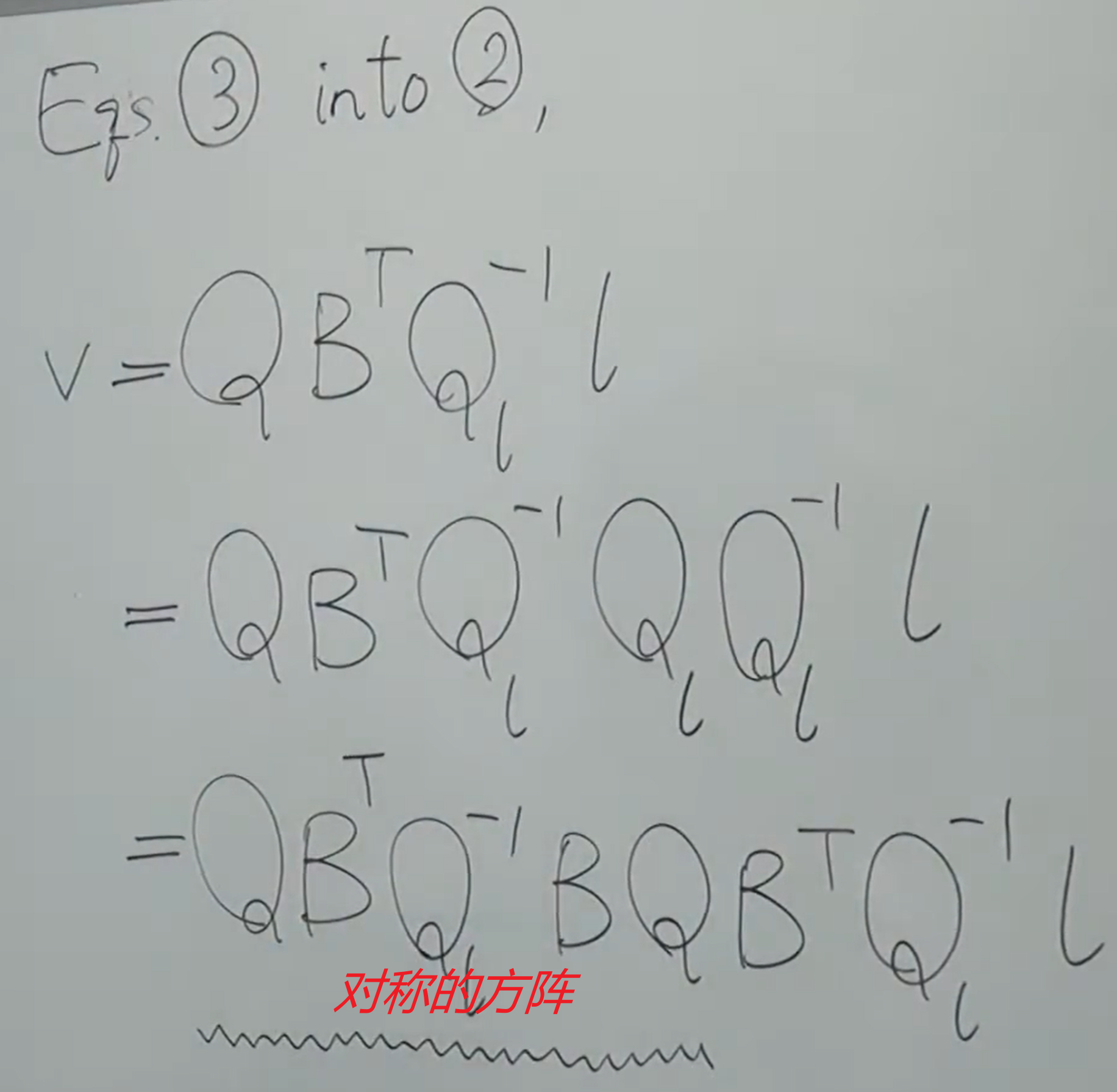





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
2019-07-14 matlab的拟合函数polyfit()函数